Калькулятор форвардных курсов – Investing.com. Форвардный курс валюты

Форвардный валютный курс

Форвардный валютный курс (англ. forward exchange rate) – это цена валюты при отсроченной поставке.

Пример форвардной сделки: допустим, участник валютного рынка (импортер) для оплаты договора нуждается в сумме равной 10 000 долларов США. Для этого он должен продать 7142 евро (курс EUR = USD 1.4001. В одном случае импортер может заключить срочную сделку обмена евро на доллар по курсу спот и положить доллары на трехмесячный депозит в американском банке под 3% годовых, получив дополнительно 75 USD.

В другом случае для импортера целесообразно положить евро в европейский банк на 3 месяца под 4,5% годовых, а после истечения периода договора купить необходимые доллары. В этом случае импортер сможет дополнительно заработать 80 долларов. Таким образом, чтобы купить 10 тысяч евро ему, при прежнем курсе необходима меньшая сумма долларов.

Всегда действия импортера направлены на снижение курса валюты. Опасаясь его повышения, он может обратиться в банк и приобрести эту валюту с поставочным сроком, приближенным к сроку платежа. Форвардная сделка будет совершена по форвард-курсу, который часто выше спот-курса. В данном случае импортер понесет дополнительные затраты, являющиеся по сути платой за страховку. Обычно форвардный курс превышает спот-курс настолько, насколько банковские ставки котируемой валюты ниже ставок контрагентной валюты.

Форвардный обменный курс

Данный курс определен для поставки валюты сегодня в определенной дате в будущем. В банковской практике форвардный обменный курс определяется двумя способами:

На межбанковском рынке часто устанавливается лишь дисконт или премия, которые, соответственно, вычитаются или прибавляются из курса сделки спот, т.к. размер премии или скидки стабильнее относительно спот-курса. Данный способ называется Swap.
Форвардный курс котируется в цифровом целом выражении – курс Outright.

Расчет форвардного валютного курса. Swap метод

Вначале рассчитывается размер премии или дисконта исходя из процентных банковских ставок по депозитам:

Где: D – дисконт; P – премия; S(i/j) – курс спот; n – срок форварда; Rj, Ri – процентные ставки по депозитам в валюте j и I соответсвенно.

Размер форвардного валютного курса определяется путем прибавления к курсу спот премии или вычитанием из спот курса дисконта. В биржевых бюллетенях всегда публикуются форвардные курсы на разные сроки, которые рассчитаны с использованием процентных ставок ЛИБОР. В случае сопоставления эффективности размещения инвестиции по форвардному курсу на международном и на внутреннем валютном рынке форвардный курс может определяться как отношение процентных ставок, взятых по межбанковскому кредиту, умноженному на спот-курс.

Форвардный курс может рассчитываться по формуле:

Где: L – ставка ЛИБОР; Fn(i/j) – форвардный валютный курс; S(i/j) – текущий спот-курс; R – процентная ставка на межбанковском внутреннем рынке.

forex-investor.net

Калькулятор форвардных курсов – Investing.com

Главные новости

1д1н1м6м1г5лМакс.

Нефть Brent	74,86	+0,41	+0,55%
Нефть WTI	70,56	+0,23	+0,33%
Золото	1.241,80	-4,80	-0,39%
Серебро	15,835	-0,142	-0,89%
Платина	831,70	-14,70	-1,74%
Палладий	932,80	-16,00	-1,69%
Природный газ	2,758	-0,039	-1,39%
Алюминий	2.039,75	-3,50	-0,17%

USD/RUB	62,5553	+0,2880	+0,46%
EUR/USD	1,1686	+0,0015	+0,13%
GBP/USD	1,3236	+0,0031	+0,23%
USD/CAD	1,3162	+0,0008	+0,06%
USD/JPY	112,38	-0,14	-0,12%
AUD/USD	0,7423	+0,0014	+0,19%
GBP/JPY	148,70	+0,08	+0,05%
EUR/RUB	73,0744	+0,4244	+0,58%

РТС	1.189,35	+11,85	+1,01%
Индекс МосБиржи	2.346,43	+24,37	+1,05%
S&P 500 (F)	2.804,25	+5,75	+0,21%
Dow 30	25.019,41	+94,52	+0,38%
DAX	12.540,73	+47,76	+0,38%
FTSE 100	7.661,87	+10,54	+0,14%
Индекс USD	94,44	-0,13	-0,14%
Фьючерс на Bitcoin	6.180,0	+25,0	+0,41%

BTC/USD	6.234,1	-26,8	-0,43%
ETH/USD	433,18	-8,98	-2,03%
BCH/USD	693,50	-9,83	-1,40%
LTC/USD	76,060	-1,180	-1,53%
IOT/USD	0,96964	-0,01632	-1,66%
BTC/RUB	391.495	+638	+0,16%
XRP/USD	0,43590	-0,00634	-1,43%
DASH/USD	219,65	-7,51	-3,31%

ru.investing.com

Форвардный валютный курс — WiKi

Форвардный валютный курс (англ. forward exchange rate) — это прописанный в форвардном контракте коммерческого банка с инвестором валютный курс, по которому банк готов произвести обмен валюты в установленную будущую дату[1][2][3]. Форвардный обменный курс является видом форвардной цены. Транснациональные компании, банки и иные финансовые институты заключают форвардные контракты в целях хеджирования валютных рисков[1]. Хеджируются как кредиторская, так и дебиторская задолженности, деноминированные в иностранной валюте. Хеджирование преимущественно крупные транзакции, для малых же применяются фьючерсные контракты. Различие обусловлено тем, что форвардные сделки являются внебиржевыми и позволяют банкам точнее детализировать условия. Фьючерсные контракты, напротив, стандартизированы и торгуются на бирже[1]. Как правило, банки предлагают форвардные курсы твёрдых валют с датой поставки в один, три, шесть, девять или двенадцать месяцев. Иногда предлагаются котировки с датой поставки в пять или десять лет[2].

Форвардный валютный курс определяется на базе паритета между наличным курсом и разницей между процентными ставками двух валютных зон. Данный паритет является равновесием валютного рынка, когда возможности извлечения Арбитраж (экономика)арбитражной прибыли устраняются. Если в равновесии ставки не равны, уравнение паритета подразумевает, что форвардный курс включает премию или, наоборот, дисконт, которые отражают процентный дифференциал. Форвардные курсы составляют важный элемент теории прогнозирования будущих наличных курсов — исследователи в области финансовой экономики выдвинули гипотезу, согласно которой форвардный курс точно предсказывает наличный курс. Попытки эмпирической проверки гипотезы дали смешанные результаты.

Связь с покрытым паритетом процентных ставок

Покрытый паритет процентных ставок представляет собой условие отсутствия арбитража на валютном рынке при наличии доступа на рынок форвардов. Инвесторы заключают форвардные контракты, тем самым «покрывая» валютные риски — неожиданные скачки валютного курса. Переставив члены в уравнении покрытого паритета, можно представить форвардный курс как функцию трёх переменных: наличного курса, отечественной ставки процента и зарубежной ставки. Фактически это означает, что форвардный курс есть цена форвардного контракта, стоимость которого производна от цен на спотовые контракты и дополнительной информации об имеющихся процентных ставках[4].

Соблюдение покрытого паритета процентных ставок означает, что отечественные инвесторы безразличны между вкладом в национальной валюте и вкладом в иностранной, которая получена по наличному курсу и по истечении срока вновь обменена на отечественную по форвардному курсу. Арбитраж невозможен, поскольку доходность вкладов в национальной валюте, 1+id, равна доходности вклада в иностранной, [S/F](1+if). Если бы они не были уравнены с помощью форвардных контрактов, инвесторы могли бы зарабатывать на разнице, занимая в стране с низкой ставкой и делая вклад в валюте страны с высокой ставкой[4].

(1+id)=SF(1+if){\displaystyle (1+i_{d})={\frac {S}{F}}(1+i_{f})}

где

F — форвардный валютный курс; S — текущий наличный курс; id — процентная ставка в базовой валютной зоне; if — процентная ставка в котируемой валютной зоне.

Перенеся члены, получаем

F=S(1+if)(1+id){\displaystyle F=S{\frac {(1+i_{f})}{(1+i_{d})}}}

Форвардная премия и форвардный дисконт

Равновесие, проистекающее из отношения между форвардным и наличным курсами в контексте покрытого паритета процентных ставок, устраняет (полностью или частично) несовершенства рынка, связанные с появлением арбитража. Даже если соответствующие возможности появляются, они скоротечны. Установление равновесия при разных процентных ставках в общем случае требует отклонения форвардного курса от наличного курса. Отклонение называется премией (если форвардный курс превышает наличный курс) или дисконтом (в противном случае), выражая процентный дифференциал. Приводимые ниже выкладки демонстрируют алгоритм расчёта премии (дисконта)[1][2].

Форвардный курс отличается от наличного курса на размер премии или дисконта:

F=S(1+P){\displaystyle F=S(1+P)}

где

P — форвардная премия (больше нуля) или дисконт (меньше нуля).

Переставляя члены уравнения, имеем

P=FS−1{\displaystyle P={\frac {F}{S}}-1}

На практике форвардные премии (дисконты) выражаются как процентные (в годовом исчислении) отклонения от наличного курса. В этом случае необходимо учитывать количество дней до поставки[2]

PN=(FS−1)360d{\displaystyle P_{N}=({\frac {F}{S}}-1){\frac {360}{d}}}

где

N — срок поставки для данной котировки; d — количество дней до поставки.

Например, чтобы вычислить форвардную премию (дисконт) по котировке со сроком поставки шесть месяцев и 30 днями до истечения срока, имея наличный курс 1,2238 $/€ и форвардный курс 1,2260 $/€, необходимо решить:

P6=(1.22601.2238−1)36030=0.021572=2.16%{\displaystyle P_{6}=({\frac {1.2260}{1.2238}}-1){\frac {360}{30}}=0.021572=2.16\%}

Результат — 0,021572 — положителен, поэтому в данном случае имеет место премия. Вывод: евро торгуется с премией 2,16% по отношению к доллару.

Прогнозирование будущего наличного курса

Гипотеза о несмещённости гласит, что в условиях рациональных ожиданиях и нейтральности к риску форвардный курс является несмещённым прогнозом будущего наличного курса. В простейшем виде, без введения в уравнение премии за риск гипотеза выглядит так[3][5][6][7]:

Ft=Et(St+k){\displaystyle F_{t}=E_{t}(S_{t+k})}

где

Ft{\displaystyle F_{t}} — форвардный валютный курс в период t; k{\displaystyle k} — положительное количество периодов; Et(St+k){\displaystyle E_{t}(S_{t+k})} — ожидаемый будущий наличный курс в период t + k.

Установление причин, по которым гипотезы опровергается эмпирически, — открытая проблема финансовой науки. Однозначного подтверждения коинтеграции между форвардным и будущим наличным курсами нет, эмпирический анализ даёт смешанные результаты[5][8][9]. Регрессионный анализ позволил установить, что наблюдаемые изменения наличного курса зависят от размера форвардной премии отрицательно[10]. Авторами предложено несколько объяснений феномена. Одно из них связано с ослаблением допущения о нейтральности к риску[11].

Приведённое далее уравнение выражает демонстрирует связь между форвардным курсом и будущим наличным курсом с премией за риск (не путать с форвардной премией)[12]:

Ft=Et(St+1)+Pt{\displaystyle F_{t}=E_{t}(S_{t+1})+P_{t}}

где

Pt{\displaystyle P_{t}} — премия за риск.

Введя в уравнение текущий наличный курс, можно найти форвардный дифференциал — разницу между форвардным курсом и текущим наличным курсом:

Ft−St=Et(St+1−St)+Pt{\displaystyle F_{t}-S_{t}=E_{t}(S_{t+1}-S_{t})+P_{t}}

Юджин Фама предположил. что эмпирическое опровержение гипотезы обусловлено вариацией во времени, которую демонстрирует премия за риск. Он также допустил наличие вариации в другом компонента форвардного дифференциала — ожидаемом изменении наличного курса[12]. Многократные попытки валидации его результатов наконец показали, что гипотеза о несмещённости отвергается и на данных с варьирующейся премией за риск, и на данных с постоянной премией за риск[13]. Условное смещение также трактуют как экзогенный фактор, вызванный политикой сглаживания процентных ставок и стабилизации валютного курса. Согласно другому объяснению, избыточная доходность на форвардном рынке связана с дискретным характером изменений в экономике. Некоторые исследователи скептически воспринимали опровержение гипотезы данными, указывая на наличие противоположных результатов. Расхождение в результатах они пытались объяснить низким качеством данных и даже неверным выбором длительности форвардных контрактов[11]. Показано, что форвардный курс служит полезной прокси-переменной будущего наличного курса, чья премия за ликвидность на заре эпохи плавающих курсов в 1970-е годы в средеем равнялась нулю [14]. Тестирование структурной устойчивости коинтегрированных временных рядов наличного и форвардного курсов с помощью эндогенных разрывов подтвердило выполнение гипотезы как в краткосрочной, так и в долгосрочной перспективе[9].

Примечания

↑ 1 2 3 4 Madura, Jeff. International Financial Management: Abridged 8th Edition. — Mason, OH : Thomson South-Western, 2007. — ISBN 0-324-36563-2.
↑ 1 2 3 4 Eun, Cheol S. International Financial Management, 6th Edition. — New York, NY : McGraw-Hill/Irwin, 2011. — ISBN 978-0-07-803465-7.
↑ 1 2 Levi, Maurice D. International Finance, 4th Edition. — New York, NY : Routledge, 2005. — ISBN 978-0-415-30900-4.
↑ 1 2 Feenstra, Robert C. International Macroeconomics. — New York, NY : Worth Publishers, 2008. — ISBN 978-1-4292-0691-4.
↑ 1 2 Delcoure, Natalya (2003). «The Forward Rate Unbiasedness Hypothesis Reexamined: Evidence from a New Test». Global Finance Journal 14 (1): 83–93. DOI:10.1016/S1044-0283(03)00006-1. Проверено 2011-06-21.
↑ Ho, Tsung-Wu (2003). «A re-examination of the unbiasedness forward rate hypothesis using dynamic SUR model». The Quarterly Review of Economics and Finance 43 (3): 542–559. DOI:10.1016/S1062-9769(02)00171-0. Проверено 2011-06-23.
↑ Sosvilla-Rivero, Simón (1992). «Further tests on the forward exchange rate unbiasedness hypothesis». Economics Letters 40 (3): 325–331. DOI:10.1016/0165-1765(92)90013-O. Проверено 2011-06-27.
↑ Moffett, Michael H. Fundamentals of Multinational Finance, 3rd Edition. — Boston, MA : Addison-Wesley, 2009. — ISBN 978-0-321-54164-2.
↑ 1 2 Villanueva, O. Miguel (2007). «Spot-forward cointegration, structural breaks and FX market unbiasedness». International Financial Markets, Institutions & Money 17 (1): 58–78. DOI:10.1016/j.intfin.2005.08.007. Проверено 2011-06-22.
↑ Zivot, Eric (2000). «Cointegration and forward and spot exchange rate regressions». Journal of International Money and Finance 19 (6): 785–812. DOI:10.1016/S0261-5606(00)00031-0. Проверено 2011-06-22.
↑ 1 2 Diamandis, Panayiotis F. (2008). «Testing the forward rate unbiasedness hypothesis during the 1920s». International Financial Markets, Institutions & Money 18 (4): 358–373. DOI:10.1016/j.intfin.2007.04.003. Проверено 2011-06-23.
↑ 1 2 Fama, Eugene F. (1984). «Forward and spot exchange rates». Journal of Monetary Economics 14 (3): 319–338. DOI:10.1016/0304-3932(84)90046-1. Проверено 2011-06-20.
↑ Chatterjee, Devalina (2010). Three essays in forward rate unbiasedness hypothesis (Thesis). Utah State University. pp. 1–102. Retrieved 2012-06-21.
↑ Cornell, Bradford (1977). «Spot rates, forward rates and exchange market efficiency». Journal of Financial Economics 5 (1): 55–65. DOI:10.1016/0304-405X(77)90029-0. Проверено 2011-06-28.

ru-wiki.org

Форвардные курсы иностранной валюты – британского фунта

Тип операции

Цена за единицу,

$ США

Цена за $ 1 США

Среда

Четверг

Среда

четверг

Спот

30-дневный форвард

90-дневный форвард

180-дневный форвард

1,6099

1,6068

1,6004

1,5911

1,6124

1,6091

1,6030

1,5934

0,6212

0,6224

0,6248

0,6285

0,6202

0,6215

0,6238

0,6276

На форвардном рынке заключаются следующие виды контрактов: форвардные валютные контракты, фьючерсные контракты, опционные контракты и своп-контракты.

Форвардный валютный контракт – это обязательное для исполнения соглашение между банком и клиентом по покупке или продаже в определенный день в будущем определенной суммы иностранной валюты. В этом контракте валюта, сумма, обменный курс и дата платежа фиксируются в момент заключения сделки. Валютный курс форвардной сделки называется форвардным курсом. Он является срочным. Срок форвардных сделок колеблется от 3 дней до 5 лет, однако наиболее распространенными сроками являются 1, 3, 6 и 9 месяцев.

Форвардный контракт является банковским нестандартизованным контрактом, поэтому он может быть составлен с учетом интересов клиентов. Форвардный рынок сделок до 6 месяцев в основных валютах достаточно стабилен, на срок более 6 месяцев – недостаточно устойчив, поскольку отдельные операции могут вызвать сильные колебания обменных курсов. Форвардный курс (FR) иностранной валюты во многих случаях отличается от ее спот-курса (SR). Если FR > SR, то валюта продается с форвардной надбавкой, или форвардной премией (forward premium) Форвардная премия или форвардная надбавка – разность между форвардной и спотовой ценой валюты, выраженная в виде процента в годовом исчислении. Если FR < SR, то валюта продается с форвардной скидкой, или форвардным дисконтом форвардный дисконт, или форвардная скидка (forward discount) – разность между форвардной и спотовой ценой валюты, выраженная в виде процента в годовом исчислении.

Размер форвардной премии или форвардного дисконта определяется по формуле:

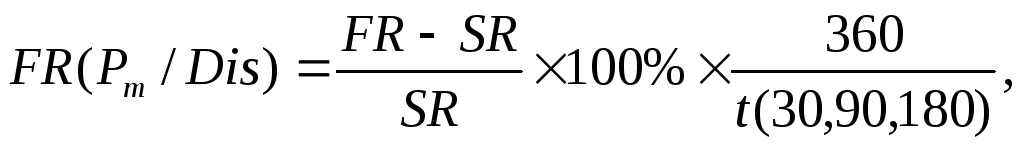
где:

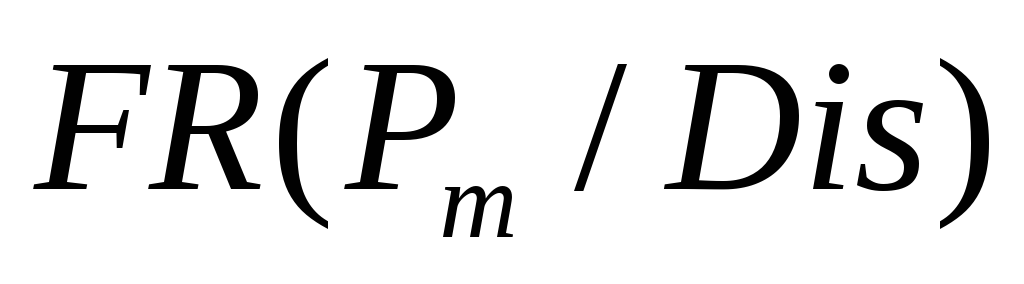- форвардная премия или дисконт;

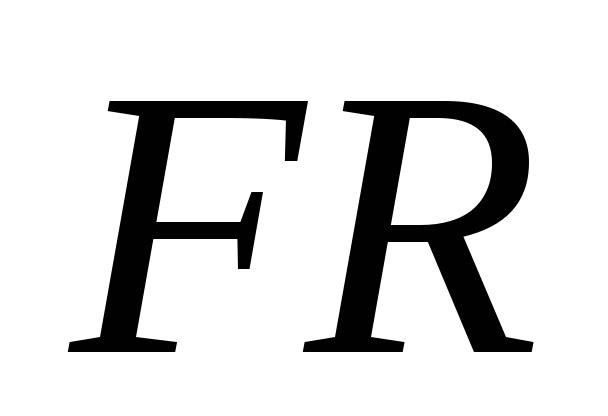- форвардный курс;

- спотовый курс;

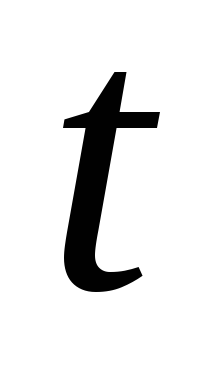- срок форвардного контракта.

Ежедневно ведущие финансовые газеты мира (например, Wall Street Jornal) печатают текущий (спотовый) курс (spot rate) и форвардный курс (forward rate) основных мировых валют на 30, 90 и 180 дней вперед.

На форвардном рынке банки также котируют курсы покупки (Bid rate – BR) и курсы продажи валют (Ask rate – AR) и, соответственно, рассчитывают кросс-курсы. При этом маржа между AR и BR больше при форвардных операциях и составляет 1/8 – 1/4 годовых от курса спот в пересчете на срок сделки. Кросс-курс – курс обмена между двумя валютами, полученный из их отношения к третьей валюте, обычно $ США.

Существует два основных метода котировки форвардного курса: метод аутрайт и метод своп-ставок. При котировке метода аутрайт банки указывают как полный спот-курс, так и полный форвардный курс, а также сумму и срок поставки валюты. При котировке методом своп-ставок определяется только премия или дисконт, которые при прямой котировке соответственно прибавляются к курсу спот или вычитаются из него. Своп-ставки выражаются в абсолютных долях соответствующей валюты по отношению к американскому доллару, аналогично котированию spot.

Прямая котировка – выражение стоимости единицы иностранной валюты в единицах национальной, обратная котировка – выражение стоимости единицы национальной валюты в определенном количестве иностранной. Наиболее широко используется прямая котировка. Например, 8 грн. за $ 1 – прямая котировка доллара США на украинском рынке.

Размер ставки своп определяется исключительно различным уровнем процентных ставок валют стран и рассчитывается по формуле:

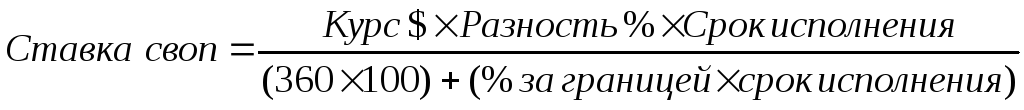
Форвардный курс (FR) и спот-курс (SR) тесно связаны между собой. Форвардный курс представляет собой совокупный рыночный прогноз спот-курса валюты в будущем. Следовательно, форвардная цена помогает международным компаниям прогнозировать будущие изменения валютных курсов. Эти изменения могут повлиять на цену экспортируемых компонентов, используемых для производства продукции, а также на конкурентоспособность компании и прибыльность ее экспортных операций. Если валюта продается с форвардной скидкой, участники валютного рынка испытывают уверенность в том, что с течением времени обменный курс этой валюты снизится. В таком случае компании могут сократить свои активы или увеличить обязательства, выраженные в этой валюте. Валюта стран, которые имеют торговый дефицит платежного баланса или высокий уровень инфляции, продается с форвардной скидкой. Если валюта продается с форвардной надбавкой, на валютном рынке существует уверенность в том, что с течением времени обменный курс этой валюты повысится. В таком случае компании могут увеличить свои активы или сократить свои обязательства, выраженные в этой валюте. Валюта стран, в которых имеет место положительное сальдо торгового баланса или низкий уровень инфляции, в большинстве случаев продается с форвардной надбавкой. Таким образом, разница между спот-курсом и форвардным курсом валюты той или иной страны во многих случаях определяет рыночные ожидания в отношении экономической политики этой страны.

Основное назначение форвардных операций заключается в хеджировании валютного риска. С помощью форвардных контрактов международные компании стремятся закрыть открытую валютную позицию.

Фьючерсный контракт – это обязательное для исполнения соглашение между биржей и клиентом по покупке или продаже в определенный день в будущем определенной суммы иностранной валюты. Сущность фьючерских операций сходна с форвардными сделками. Однако при наличии сходных характеристик (фиксированная валюта, сумма, обменный курс и дата платежа) фьючерсные операции имеют существенные отличия от форвардных сделок:

Фьючерские операции осуществляются на биржевом рынке, форвардные – на межбанковском рынке. Сроки исполнения фьючерских контрактов привязаны к определенным датам (например, третья среда каждого месяца) и стандартизованы по срокам, объемам и условиям поставки. В форвардных контрактах сроки и объемы сделки определяются по взаимной договоренности сторон.
Фьючерские операции осуществляются с ограниченным кругом валют (доллар США, евро, японская иена, фунт стерлингов и др.). При формировании форвардного контракта круг валют существенно шире.
Фьючерсный рынок доступен как для крупных инвесторов, так и для индивидуальных и мелких институциональных инвесторов. Минимальная сумма для заключения форвардного контракта составляет в ряде случаев $ 500 тыс.
Фьючерские операции на 95 % заканчиваются заключением офсетной сделки, при этом реальной поставки валюты не осуществляется, а участники данной операции получают лишь разницу между первоначальной ценой заключения контракта и существующей в день совершения обратной сделки. При форвардах 95 % всех сделок заканчиваются поставкой валюты по контракту.
Стандартизация контрактов означает, что фьючерсные сделки могут совершаться более дешево, чем индивидуально заключаемые между клиентом и банком форвардные сделки. Форвардные сделки могут привести к большим затратам для клиента при закрытии позиций.

Основные различия между форвардными и фьючерсными контрактами представлены в табл. 1.15.

Таблица 1.15.

studfiles.net

Форвардный валютный курс — Википедия

Форвардный валютный курс (англ. forward exchange rate) — это прописанный в форвардном контракте коммерческого банка с инвестором валютный курс, по которому банк готов произвести обмен валюты в установленную будущую дату[1][2][3]. Форвардный обменный курс является видом форвардной цены. Транснациональные компании, банки и иные финансовые институты заключают форвардные контракты в целях хеджирования валютных рисков[1]. Хеджируются как кредиторская, так и дебиторская задолженности, деноминированные в иностранной валюте. Хеджирование преимущественно крупные транзакции, для малых же применяются фьючерсные контракты. Различие обусловлено тем, что форвардные сделки являются внебиржевыми и позволяют банкам точнее детализировать условия. Фьючерсные контракты, напротив, стандартизированы и торгуются на бирже[1]. Как правило, банки предлагают форвардные курсы твёрдых валют с датой поставки в один, три, шесть, девять или двенадцать месяцев. Иногда предлагаются котировки с датой поставки в пять или десять лет[2].

Форвардный валютный курс определяется на базе паритета между наличным курсом и разницей между процентными ставками двух валютных зон. Данный паритет является равновесием валютного рынка, когда возможности извлечения Арбитраж (экономика)арбитражной прибыли устраняются. Если в равновесии ставки не равны, уравнение паритета подразумевает, что форвардный курс включает премию или, наоборот, дисконт, которые отражают процентный дифференциал. Форвардные курсы составляют важный элемент теории прогнозирования будущих наличных курсов — исследователи в области финансовой экономики выдвинули гипотезу, согласно которой форвардный курс точно предсказывает наличный курс. Попытки эмпирической проверки гипотезы дали смешанные результаты.

Содержание

Связь с покрытым паритетом процентных ставокПравить

Покрытый паритет процентных ставок представляет собой условие отсутствия арбитража на валютном рынке при наличии доступа на рынок форвардов. Инвесторы заключают форвардные контракты, тем самым «покрывая» валютные риски — неожиданные скачки валютного курса. Переставив члены в уравнении покрытого паритета, можно представить форвардный курс как функцию трёх переменных: наличного курса, отечественной ставки процента и зарубежной ставки. Фактически это означает, что форвардный курс есть цена форвардного контракта, стоимость которого производна от цен на спотовые контракты и дополнительной информации об имеющихся процентных ставках[4].

Соблюдение покрытого паритета процентных ставок означает, что отечественные инвесторы безразличны между вкладом в национальной валюте и вкладом в иностранной, которая получена по наличному курсу и по истечении срока вновь обменена на отечественную по форвардному курсу. Арбитраж невозможен, поскольку доходность вкладов в национальной валюте, 1+id, равна доходности вклада в иностранной, [S/F](1+if). Если бы они не были уравнены с помощью форвардных контрактов, инвесторы могли бы зарабатывать на разнице, занимая в стране с низкой ставкой и делая вклад в валюте страны с высокой ставкой[4].

(1+id)=SF(1+if){\displaystyle (1+i_{d})={\frac {S}{F}}(1+i_{f})}

где

F — форвардный валютный курс; S — текущий наличный курс; id — процентная ставка в базовой валютной зоне; if — процентная ставка в котируемой валютной зоне.

Перенеся члены, получаем

F=S(1+if)(1+id){\displaystyle F=S{\frac {(1+i_{f})}{(1+i_{d})}}}

Форвардная премия и форвардный дисконтПравить

Равновесие, проистекающее из отношения между форвардным и наличным курсами в контексте покрытого паритета процентных ставок, устраняет (полностью или частично) несовершенства рынка, связанные с появлением арбитража. Даже если соответствующие возможности появляются, они скоротечны. Установление равновесия при разных процентных ставках в общем случае требует отклонения форвардного курса от наличного курса. Отклонение называется премией (если форвардный курс превышает наличный курс) или дисконтом (в противном случае), выражая процентный дифференциал. Приводимые ниже выкладки демонстрируют алгоритм расчёта премии (дисконта)[1][2].

Форвардный курс отличается от наличного курса на размер премии или дисконта:

F=S(1+P){\displaystyle F=S(1+P)}

где

P — форвардная премия (больше нуля) или дисконт (меньше нуля).

Переставляя члены уравнения, имеем

P=FS−1{\displaystyle P={\frac {F}{S}}-1}

На практике форвардные премии (дисконты) выражаются как процентные (в годовом исчислении) отклонения от наличного курса. В этом случае необходимо учитывать количество дней до поставки[2]

PN=(FS−1)360d{\displaystyle P_{N}=({\frac {F}{S}}-1){\frac {360}{d}}}

где

N — срок поставки для данной котировки; d — количество дней до поставки.

Например, чтобы вычислить форвардную премию (дисконт) по котировке со сроком поставки шесть месяцев и 30 днями до истечения срока, имея наличный курс 1,2238 $/€ и форвардный курс 1,2260 $/€, необходимо решить:

P6=(1.22601.2238−1)36030=0.021572=2.16%{\displaystyle P_{6}=({\frac {1.2260}{1.2238}}-1){\frac {360}{30}}=0.021572=2.16\%}

Результат — 0,021572 — положителен, поэтому в данном случае имеет место премия. Вывод: евро торгуется с премией 2,16% по отношению к доллару.

Прогнозирование будущего наличного курсаПравить

Гипотеза о несмещённости гласит, что в условиях рациональных ожиданиях и нейтральности к риску форвардный курс является несмещённым прогнозом будущего наличного курса. В простейшем виде, без введения в уравнение премии за риск гипотеза выглядит так[3][5][6][7]:

Ft=Et(St+k){\displaystyle F_{t}=E_{t}(S_{t+k})}

где

Ft{\displaystyle F_{t}} — форвардный валютный курс в период t; k{\displaystyle k} — положительное количество периодов; Et(St+k){\displaystyle E_{t}(S_{t+k})} — ожидаемый будущий наличный курс в период t + k.

Установление причин, по которым гипотезы опровергается эмпирически, — открытая проблема финансовой науки. Однозначного подтверждения коинтеграции между форвардным и будущим наличным курсами нет, эмпирический анализ даёт смешанные результаты[5][8][9]. Регрессионный анализ позволил установить, что наблюдаемые изменения наличного курса зависят от размера форвардной премии отрицательно[10]. Авторами предложено несколько объяснений феномена. Одно из них связано с ослаблением допущения о нейтральности к риску[11].

Приведённое далее уравнение выражает демонстрирует связь между форвардным курсом и будущим наличным курсом с премией за риск (не путать с форвардной премией)[12]:

Ft=Et(St+1)+Pt{\displaystyle F_{t}=E_{t}(S_{t+1})+P_{t}}

где

Pt{\displaystyle P_{t}} — премия за риск.

Введя в уравнение текущий наличный курс, можно найти форвардный дифференциал — разницу между форвардным курсом и текущим наличным курсом:

Ft−St=Et(St+1−St)+Pt{\displaystyle F_{t}-S_{t}=E_{t}(S_{t+1}-S_{t})+P_{t}}

Юджин Фама предположил. что эмпирическое опровержение гипотезы обусловлено вариацией во времени, которую демонстрирует премия за риск. Он также допустил наличие вариации в другом компонента форвардного дифференциала — ожидаемом изменении наличного курса[12]. Многократные попытки валидации его результатов наконец показали, что гипотеза о несмещённости отвергается и на данных с варьирующейся премией за риск, и на данных с постоянной премией за риск[13]. Условное смещение также трактуют как экзогенный фактор, вызванный политикой сглаживания процентных ставок и стабилизации валютного курса. Согласно другому объяснению, избыточная доходность на форвардном рынке связана с дискретным характером изменений в экономике. Некоторые исследователи скептически воспринимали опровержение гипотезы данными, указывая на наличие противоположных результатов. Расхождение в результатах они пытались объяснить низким качеством данных и даже неверным выбором длительности форвардных контрактов[11]. Показано, что форвардный курс служит полезной прокси-переменной будущего наличного курса, чья премия за ликвидность на заре эпохи плавающих курсов в 1970-е годы в средеем равнялась нулю [14]. Тестирование структурной устойчивости коинтегрированных временных рядов наличного и форвардного курсов с помощью эндогенных разрывов подтвердило выполнение гипотезы как в краткосрочной, так и в долгосрочной перспективе[9].

↑ 1 2 3 4 Madura, Jeff. International Financial Management: Abridged 8th Edition. — Mason, OH : Thomson South-Western, 2007. — ISBN 0-324-36563-2.
↑ 1 2 3 4 Eun, Cheol S. International Financial Management, 6th Edition. — New York, NY : McGraw-Hill/Irwin, 2011. — ISBN 978-0-07-803465-7.
↑ 1 2 Levi, Maurice D. International Finance, 4th Edition. — New York, NY : Routledge, 2005. — ISBN 978-0-415-30900-4.
↑ 1 2 Feenstra, Robert C. International Macroeconomics. — New York, NY : Worth Publishers, 2008. — ISBN 978-1-4292-0691-4.
↑ 1 2 Delcoure, Natalya (2003). «The Forward Rate Unbiasedness Hypothesis Reexamined: Evidence from a New Test». Global Finance Journal 14 (1): 83–93. DOI:10.1016/S1044-0283(03)00006-1. Проверено 2011-06-21.
↑ Ho, Tsung-Wu (2003). «A re-examination of the unbiasedness forward rate hypothesis using dynamic SUR model». The Quarterly Review of Economics and Finance 43 (3): 542–559. DOI:10.1016/S1062-9769(02)00171-0. Проверено 2011-06-23.
↑ Sosvilla-Rivero, Simón (1992). «Further tests on the forward exchange rate unbiasedness hypothesis». Economics Letters 40 (3): 325–331. DOI:10.1016/0165-1765(92)90013-O. Проверено 2011-06-27.
↑ Moffett, Michael H. Fundamentals of Multinational Finance, 3rd Edition. — Boston, MA : Addison-Wesley, 2009. — ISBN 978-0-321-54164-2.
↑ 1 2 Villanueva, O. Miguel (2007). «Spot-forward cointegration, structural breaks and FX market unbiasedness». International Financial Markets, Institutions & Money 17 (1): 58–78. DOI:10.1016/j.intfin.2005.08.007. Проверено 2011-06-22.
↑ Zivot, Eric (2000). «Cointegration and forward and spot exchange rate regressions». Journal of International Money and Finance 19 (6): 785–812. DOI:10.1016/S0261-5606(00)00031-0. Проверено 2011-06-22.
↑ 1 2 Diamandis, Panayiotis F. (2008). «Testing the forward rate unbiasedness hypothesis during the 1920s». International Financial Markets, Institutions & Money 18 (4): 358–373. DOI:10.1016/j.intfin.2007.04.003. Проверено 2011-06-23.
↑ 1 2 Fama, Eugene F. (1984). «Forward and spot exchange rates». Journal of Monetary Economics 14 (3): 319–338. DOI:10.1016/0304-3932(84)90046-1. Проверено 2011-06-20.
↑ Chatterjee, Devalina (2010). Three essays in forward rate unbiasedness hypothesis (Thesis). Utah State University. pp. 1–102. Retrieved 2012-06-21.
↑ Cornell, Bradford (1977). «Spot rates, forward rates and exchange market efficiency». Journal of Financial Economics 5 (1): 55–65. DOI:10.1016/0304-405X(77)90029-0. Проверено 2011-06-28.

ru.mobile.bywiki.com

Форвардный валютный курс Википедия

Форвардный валютный курс (англ. forward exchange rate) — это прописанный в форвардном контракте коммерческого банка с инвестором валютный курс, по которому банк готов произвести обмен валюты в установленную будущую дату[1][2][3]. Форвардный обменный курс является видом форвардной цены. Транснациональные компании, банки и иные финансовые институты заключают форвардные контракты в целях хеджирования валютных рисков[1]. Хеджируются как кредиторская, так и дебиторская задолженности, деноминированные в иностранной валюте. Хеджирование преимущественно крупные транзакции, для малых же применяются фьючерсные контракты. Различие обусловлено тем, что форвардные сделки являются внебиржевыми и позволяют банкам точнее детализировать условия. Фьючерсные контракты, напротив, стандартизированы и торгуются на бирже[1]. Как правило, банки предлагают форвардные курсы твёрдых валют с датой поставки в один, три, шесть, девять или двенадцать месяцев. Иногда предлагаются котировки с датой поставки в пять или десять лет[2].

Форвардный валютный курс определяется на базе паритета между наличным курсом и разницей между процентными ставками двух валютных зон. Данный паритет является равновесием валютного рынка, когда возможности извлечения Арбитраж (экономика)арбитражной прибыли устраняются. Если в равновесии ставки не равны, уравнение паритета подразумевает, что форвардный курс включает премию или, наоборот, дисконт, которые отражают процентный дифференциал. Форвардные курсы составляют важный элемент теории прогнозирования будущих наличных курсов — исследователи в области финансовой экономики выдвинули гипотезу, согласно которой форвардный курс точно предсказывает наличный курс. Попытки эмпирической проверки гипотезы дали смешанные результаты.

Связь с покрытым паритетом процентных ставок

Покрытый паритет процентных ставок представляет собой условие отсутствия арбитража на валютном рынке при наличии доступа на рынок форвардов. Инвесторы заключают форвардные контракты, тем самым «покрывая» валютные риски — неожиданные скачки валютного курса. Переставив члены в уравнении покрытого паритета, можно представить форвардный курс как функцию трёх переменных: наличного курса, отечественной ставки процента и зарубежной ставки. Фактически это означает, что форвардный курс есть цена форвардного контракта, стоимость которого производна от цен на спотовые контракты и дополнительной информации об имеющихся процентных ставках[4].

Соблюдение покрытого паритета процентных ставок означает, что отечественные инвесторы безразличны между вкладом в национальной валюте и вкладом в иностранной, которая получена по наличному курсу и по истечении срока вновь обменена на отечественную по форвардному курсу. Арбитраж невозможен, поскольку доходность вкладов в национальной валюте, 1+id, равна доходности вклада в иностранной, [S/F](1+if). Если бы они не были уравнены с помощью форвардных контрактов, инвесторы могли бы зарабатывать на разнице, занимая в стране с низкой ставкой и делая вклад в валюте страны с высокой ставкой[4].

(1+id)=SF(1+if){\displaystyle (1+i_{d})={\frac {S}{F}}(1+i_{f})}

где

F — форвардный валютный курс; S — текущий наличный курс; id — процентная ставка в базовой валютной зоне; if — процентная ставка в котируемой валютной зоне.

Перенеся члены, получаем

F=S(1+if)(1+id){\displaystyle F=S{\frac {(1+i_{f})}{(1+i_{d})}}}

Форвардная премия и форвардный дисконт

Равновесие, проистекающее из отношения между форвардным и наличным курсами в контексте покрытого паритета процентных ставок, устраняет (полностью или частично) несовершенства рынка, связанные с появлением арбитража. Даже если соответствующие возможности появляются, они скоротечны. Установление равновесия при разных процентных ставках в общем случае требует отклонения форвардного курса от наличного курса. Отклонение называется премией (если форвардный курс превышает наличный курс) или дисконтом (в противном случае), выражая процентный дифференциал. Приводимые ниже выкладки демонстрируют алгоритм расчёта премии (дисконта)[1][2].

Форвардный курс отличается от наличного курса на размер премии или дисконта:

F=S(1+P){\displaystyle F=S(1+P)}

где

P — форвардная премия (больше нуля) или дисконт (меньше нуля).

Переставляя члены уравнения, имеем

P=FS−1{\displaystyle P={\frac {F}{S}}-1}

На практике форвардные премии (дисконты) выражаются как процентные (в годовом исчислении) отклонения от наличного курса. В этом случае необходимо учитывать количество дней до поставки[2]

PN=(FS−1)360d{\displaystyle P_{N}=({\frac {F}{S}}-1){\frac {360}{d}}}

где

N — срок поставки для данной котировки; d — количество дней до поставки.

Например, чтобы вычислить форвардную премию (дисконт) по котировке со сроком поставки шесть месяцев и 30 днями до истечения срока, имея наличный курс 1,2238 $/€ и форвардный курс 1,2260 $/€, необходимо решить:

P6=(1.22601.2238−1)36030=0.021572=2.16%{\displaystyle P_{6}=({\frac {1.2260}{1.2238}}-1){\frac {360}{30}}=0.021572=2.16\%}

Результат — 0,021572 — положителен, поэтому в данном случае имеет место премия. Вывод: евро торгуется с премией 2,16% по отношению к доллару.

Прогнозирование будущего наличного курса

Гипотеза о несмещённости гласит, что в условиях рациональных ожиданиях и нейтральности к риску форвардный курс является несмещённым прогнозом будущего наличного курса. В простейшем виде, без введения в уравнение премии за риск гипотеза выглядит так[3][5][6][7]:

Ft=Et(St+k){\displaystyle F_{t}=E_{t}(S_{t+k})}

где

Ft{\displaystyle F_{t}} — форвардный валютный курс в период t; k{\displaystyle k} — положительное количество периодов; Et(St+k){\displaystyle E_{t}(S_{t+k})} — ожидаемый будущий наличный курс в период t + k.

Установление причин, по которым гипотезы опровергается эмпирически, — открытая проблема финансовой науки. Однозначного подтверждения коинтеграции между форвардным и будущим наличным курсами нет, эмпирический анализ даёт смешанные результаты[5][8][9]. Регрессионный анализ позволил установить, что наблюдаемые изменения наличного курса зависят от размера форвардной премии отрицательно[10]. Авторами предложено несколько объяснений феномена. Одно из них связано с ослаблением допущения о нейтральности к риску[11].

Приведённое далее уравнение выражает демонстрирует связь между форвардным курсом и будущим наличным курсом с премией за риск (не путать с форвардной премией)[12]:

Ft=Et(St+1)+Pt{\displaystyle F_{t}=E_{t}(S_{t+1})+P_{t}}

где

Pt{\displaystyle P_{t}} — премия за риск.

Введя в уравнение текущий наличный курс, можно найти форвардный дифференциал — разницу между форвардным курсом и текущим наличным курсом:

Ft−St=Et(St+1−St)+Pt{\displaystyle F_{t}-S_{t}=E_{t}(S_{t+1}-S_{t})+P_{t}}

Юджин Фама предположил. что эмпирическое опровержение гипотезы обусловлено вариацией во времени, которую демонстрирует премия за риск. Он также допустил наличие вариации в другом компонента форвардного дифференциала — ожидаемом изменении наличного курса[12]. Многократные попытки валидации его результатов наконец показали, что гипотеза о несмещённости отвергается и на данных с варьирующейся премией за риск, и на данных с постоянной премией за риск[13]. Условное смещение также трактуют как экзогенный фактор, вызванный политикой сглаживания процентных ставок и стабилизации валютного курса. Согласно другому объяснению, избыточная доходность на форвардном рынке связана с дискретным характером изменений в экономике. Некоторые исследователи скептически воспринимали опровержение гипотезы данными, указывая на наличие противоположных результатов. Расхождение в результатах они пытались объяснить низким качеством данных и даже неверным выбором длительности форвардных контрактов[11]. Показано, что форвардный курс служит полезной прокси-переменной будущего наличного курса, чья премия за ликвидность на заре эпохи плавающих курсов в 1970-е годы в средеем равнялась нулю [14]. Тестирование структурной устойчивости коинтегрированных временных рядов наличного и форвардного курсов с помощью эндогенных разрывов подтвердило выполнение гипотезы как в краткосрочной, так и в долгосрочной перспективе[9].

Примечания

↑ 1 2 3 4 Madura, Jeff. International Financial Management: Abridged 8th Edition. — Mason, OH : Thomson South-Western, 2007. — ISBN 0-324-36563-2.
↑ 1 2 3 4 Eun, Cheol S. International Financial Management, 6th Edition. — New York, NY : McGraw-Hill/Irwin, 2011. — ISBN 978-0-07-803465-7.
↑ 1 2 Levi, Maurice D. International Finance, 4th Edition. — New York, NY : Routledge, 2005. — ISBN 978-0-415-30900-4.
↑ 1 2 Feenstra, Robert C. International Macroeconomics. — New York, NY : Worth Publishers, 2008. — ISBN 978-1-4292-0691-4.
↑ 1 2 Delcoure, Natalya (2003). «The Forward Rate Unbiasedness Hypothesis Reexamined: Evidence from a New Test». Global Finance Journal 14 (1): 83–93. DOI:10.1016/S1044-0283(03)00006-1. Проверено 2011-06-21.
↑ Ho, Tsung-Wu (2003). «A re-examination of the unbiasedness forward rate hypothesis using dynamic SUR model». The Quarterly Review of Economics and Finance 43 (3): 542–559. DOI:10.1016/S1062-9769(02)00171-0. Проверено 2011-06-23.
↑ Sosvilla-Rivero, Simón (1992). «Further tests on the forward exchange rate unbiasedness hypothesis». Economics Letters 40 (3): 325–331. DOI:10.1016/0165-1765(92)90013-O. Проверено 2011-06-27.
↑ Moffett, Michael H. Fundamentals of Multinational Finance, 3rd Edition. — Boston, MA : Addison-Wesley, 2009. — ISBN 978-0-321-54164-2.
↑ 1 2 Villanueva, O. Miguel (2007). «Spot-forward cointegration, structural breaks and FX market unbiasedness». International Financial Markets, Institutions & Money 17 (1): 58–78. DOI:10.1016/j.intfin.2005.08.007. Проверено 2011-06-22.
↑ Zivot, Eric (2000). «Cointegration and forward and spot exchange rate regressions». Journal of International Money and Finance 19 (6): 785–812. DOI:10.1016/S0261-5606(00)00031-0. Проверено 2011-06-22.
↑ 1 2 Diamandis, Panayiotis F. (2008). «Testing the forward rate unbiasedness hypothesis during the 1920s». International Financial Markets, Institutions & Money 18 (4): 358–373. DOI:10.1016/j.intfin.2007.04.003. Проверено 2011-06-23.
↑ 1 2 Fama, Eugene F. (1984). «Forward and spot exchange rates». Journal of Monetary Economics 14 (3): 319–338. DOI:10.1016/0304-3932(84)90046-1. Проверено 2011-06-20.
↑ Chatterjee, Devalina (2010). Three essays in forward rate unbiasedness hypothesis (Thesis). Utah State University. pp. 1–102. Retrieved 2012-06-21.
↑ Cornell, Bradford (1977). «Spot rates, forward rates and exchange market efficiency». Journal of Financial Economics 5 (1): 55–65. DOI:10.1016/0304-405X(77)90029-0. Проверено 2011-06-28.

wikiredia.ru

Форвардный валютный курс — Википедия

Форвардный валютный курс (англ. forward exchange rate) — это прописанный в форвардном контракте коммерческого банка с инвестором валютный курс, по которому банк готов произвести обмен валюты в установленную будущую дату[1][2][3]. Форвардный обменный курс является видом форвардной цены. Транснациональные компании, банки и иные финансовые институты заключают форвардные контракты в целях хеджирования валютных рисков[1]. Хеджируются как кредиторская, так и дебиторская задолженности, деноминированные в иностранной валюте. Хеджирование преимущественно крупные транзакции, для малых же применяются фьючерсные контракты. Различие обусловлено тем, что форвардные сделки являются внебиржевыми и позволяют банкам точнее детализировать условия. Фьючерсные контракты, напротив, стандартизированы и торгуются на бирже[1]. Как правило, банки предлагают форвардные курсы твёрдых валют с датой поставки в один, три, шесть, девять или двенадцать месяцев. Иногда предлагаются котировки с датой поставки в пять или десять лет[2].

Форвардный валютный курс определяется на базе паритета между наличным курсом и разницей между процентными ставками двух валютных зон. Данный паритет является равновесием валютного рынка, когда возможности извлечения Арбитраж (экономика)арбитражной прибыли устраняются. Если в равновесии ставки не равны, уравнение паритета подразумевает, что форвардный курс включает премию или, наоборот, дисконт, которые отражают процентный дифференциал. Форвардные курсы составляют важный элемент теории прогнозирования будущих наличных курсов — исследователи в области финансовой экономики выдвинули гипотезу, согласно которой форвардный курс точно предсказывает наличный курс. Попытки эмпирической проверки гипотезы дали смешанные результаты.

Связь с покрытым паритетом процентных ставок[править | править код]

Покрытый паритет процентных ставок представляет собой условие отсутствия арбитража на валютном рынке при наличии доступа на рынок форвардов. Инвесторы заключают форвардные контракты, тем самым «покрывая» валютные риски — неожиданные скачки валютного курса. Переставив члены в уравнении покрытого паритета, можно представить форвардный курс как функцию трёх переменных: наличного курса, отечественной ставки процента и зарубежной ставки. Фактически это означает, что форвардный курс есть цена форвардного контракта, стоимость которого производна от цен на спотовые контракты и дополнительной информации об имеющихся процентных ставках[4].

Соблюдение покрытого паритета процентных ставок означает, что отечественные инвесторы безразличны между вкладом в национальной валюте и вкладом в иностранной, которая получена по наличному курсу и по истечении срока вновь обменена на отечественную по форвардному курсу. Арбитраж невозможен, поскольку доходность вкладов в национальной валюте, 1+id, равна доходности вклада в иностранной, [S/F](1+if). Если бы они не были уравнены с помощью форвардных контрактов, инвесторы могли бы зарабатывать на разнице, занимая в стране с низкой ставкой и делая вклад в валюте страны с высокой ставкой[4].

(1+id)=SF(1+if){\displaystyle (1+i_{d})={\frac {S}{F}}(1+i_{f})}

где

F — форвардный валютный курс; S — текущий наличный курс; id — процентная ставка в базовой валютной зоне; if — процентная ставка в котируемой валютной зоне.

Перенеся члены, получаем

F=S(1+if)(1+id){\displaystyle F=S{\frac {(1+i_{f})}{(1+i_{d})}}}

Форвардная премия и форвардный дисконт[править | править код]

Равновесие, проистекающее из отношения между форвардным и наличным курсами в контексте покрытого паритета процентных ставок, устраняет (полностью или частично) несовершенства рынка, связанные с появлением арбитража. Даже если соответствующие возможности появляются, они скоротечны. Установление равновесия при разных процентных ставках в общем случае требует отклонения форвардного курса от наличного курса. Отклонение называется премией (если форвардный курс превышает наличный курс) или дисконтом (в противном случае), выражая процентный дифференциал. Приводимые ниже выкладки демонстрируют алгоритм расчёта премии (дисконта)[1][2].

Форвардный курс отличается от наличного курса на размер премии или дисконта:

F=S(1+P){\displaystyle F=S(1+P)}

где

P — форвардная премия (больше нуля) или дисконт (меньше нуля).

Переставляя члены уравнения, имеем

P=FS−1{\displaystyle P={\frac {F}{S}}-1}

На практике форвардные премии (дисконты) выражаются как процентные (в годовом исчислении) отклонения от наличного курса. В этом случае необходимо учитывать количество дней до поставки[2]

PN=(FS−1)360d{\displaystyle P_{N}=({\frac {F}{S}}-1){\frac {360}{d}}}

где

N — срок поставки для данной котировки; d — количество дней до поставки.

Например, чтобы вычислить форвардную премию (дисконт) по котировке со сроком поставки шесть месяцев и 30 днями до истечения срока, имея наличный курс 1,2238 $/€ и форвардный курс 1,2260 $/€, необходимо решить:

P6=(1.22601.2238−1)36030=0.021572=2.16%{\displaystyle P_{6}=({\frac {1.2260}{1.2238}}-1){\frac {360}{30}}=0.021572=2.16\%}

Результат — 0,021572 — положителен, поэтому в данном случае имеет место премия. Вывод: евро торгуется с премией 2,16% по отношению к доллару.

Прогнозирование будущего наличного курса[править | править код]

Гипотеза о несмещённости гласит, что в условиях рациональных ожиданиях и нейтральности к риску форвардный курс является несмещённым прогнозом будущего наличного курса. В простейшем виде, без введения в уравнение премии за риск гипотеза выглядит так[3][5][6][7]:

Ft=Et(St+k){\displaystyle F_{t}=E_{t}(S_{t+k})}

где

Ft{\displaystyle F_{t}} — форвардный валютный курс в период t; k{\displaystyle k} — положительное количество периодов; Et(St+k){\displaystyle E_{t}(S_{t+k})} — ожидаемый будущий наличный курс в период t + k.

Установление причин, по которым гипотезы опровергается эмпирически, — открытая проблема финансовой науки. Однозначного подтверждения коинтеграции между форвардным и будущим наличным курсами нет, эмпирический анализ даёт смешанные результаты[5][8][9]. Регрессионный анализ позволил установить, что наблюдаемые изменения наличного курса зависят от размера форвардной премии отрицательно[10]. Авторами предложено несколько объяснений феномена. Одно из них связано с ослаблением допущения о нейтральности к риску[11].

Приведённое далее уравнение выражает демонстрирует связь между форвардным курсом и будущим наличным курсом с премией за риск (не путать с форвардной премией)[12]:

Ft=Et(St+1)+Pt{\displaystyle F_{t}=E_{t}(S_{t+1})+P_{t}}

где

Pt{\displaystyle P_{t}} — премия за риск.

Введя в уравнение текущий наличный курс, можно найти форвардный дифференциал — разницу между форвардным курсом и текущим наличным курсом:

Ft−St=Et(St+1−St)+Pt{\displaystyle F_{t}-S_{t}=E_{t}(S_{t+1}-S_{t})+P_{t}}

Юджин Фама предположил. что эмпирическое опровержение гипотезы обусловлено вариацией во времени, которую демонстрирует премия за риск. Он также допустил наличие вариации в другом компонента форвардного дифференциала — ожидаемом изменении наличного курса[12]. Многократные попытки валидации его результатов наконец показали, что гипотеза о несмещённости отвергается и на данных с варьирующейся премией за риск, и на данных с постоянной премией за риск[13]. Условное смещение также трактуют как экзогенный фактор, вызванный политикой сглаживания процентных ставок и стабилизации валютного курса. Согласно другому объяснению, избыточная доходность на форвардном рынке связана с дискретным характером изменений в экономике. Некоторые исследователи скептически воспринимали опровержение гипотезы данными, указывая на наличие противоположных результатов. Расхождение в результатах они пытались объяснить низким качеством данных и даже неверным выбором длительности форвардных контрактов[11]. Показано, что форвардный курс служит полезной прокси-переменной будущего наличного курса, чья премия за ликвидность на заре эпохи плавающих курсов в 1970-е годы в средеем равнялась нулю [14]. Тестирование структурной устойчивости коинтегрированных временных рядов наличного и форвардного курсов с помощью эндогенных разрывов подтвердило выполнение гипотезы как в краткосрочной, так и в долгосрочной перспективе[9].

↑ 1 2 3 4 Madura, Jeff. International Financial Management: Abridged 8th Edition. — Mason, OH : Thomson South-Western, 2007. — ISBN 0-324-36563-2.
↑ 1 2 3 4 Eun, Cheol S. International Financial Management, 6th Edition. — New York, NY : McGraw-Hill/Irwin, 2011. — ISBN 978-0-07-803465-7.
↑ 1 2 Levi, Maurice D. International Finance, 4th Edition. — New York, NY : Routledge, 2005. — ISBN 978-0-415-30900-4.
↑ 1 2 Feenstra, Robert C. International Macroeconomics. — New York, NY : Worth Publishers, 2008. — ISBN 978-1-4292-0691-4.
↑ 1 2 Delcoure, Natalya (2003). «The Forward Rate Unbiasedness Hypothesis Reexamined: Evidence from a New Test». Global Finance Journal 14 (1): 83–93. DOI:10.1016/S1044-0283(03)00006-1. Проверено 2011-06-21.
↑ Ho, Tsung-Wu (2003). «A re-examination of the unbiasedness forward rate hypothesis using dynamic SUR model». The Quarterly Review of Economics and Finance 43 (3): 542–559. DOI:10.1016/S1062-9769(02)00171-0. Проверено 2011-06-23.
↑ Sosvilla-Rivero, Simón (1992). «Further tests on the forward exchange rate unbiasedness hypothesis». Economics Letters 40 (3): 325–331. DOI:10.1016/0165-1765(92)90013-O. Проверено 2011-06-27.
↑ Moffett, Michael H. Fundamentals of Multinational Finance, 3rd Edition. — Boston, MA : Addison-Wesley, 2009. — ISBN 978-0-321-54164-2.
↑ 1 2 Villanueva, O. Miguel (2007). «Spot-forward cointegration, structural breaks and FX market unbiasedness». International Financial Markets, Institutions & Money 17 (1): 58–78. DOI:10.1016/j.intfin.2005.08.007. Проверено 2011-06-22.
↑ Zivot, Eric (2000). «Cointegration and forward and spot exchange rate regressions». Journal of International Money and Finance 19 (6): 785–812. DOI:10.1016/S0261-5606(00)00031-0. Проверено 2011-06-22.
↑ 1 2 Diamandis, Panayiotis F. (2008). «Testing the forward rate unbiasedness hypothesis during the 1920s». International Financial Markets, Institutions & Money 18 (4): 358–373. DOI:10.1016/j.intfin.2007.04.003. Проверено 2011-06-23.
↑ 1 2 Fama, Eugene F. (1984). «Forward and spot exchange rates». Journal of Monetary Economics 14 (3): 319–338. DOI:10.1016/0304-3932(84)90046-1. Проверено 2011-06-20.
↑ Chatterjee, Devalina (2010). Three essays in forward rate unbiasedness hypothesis (Thesis). Utah State University. pp. 1–102. Retrieved 2012-06-21.
↑ Cornell, Bradford (1977). «Spot rates, forward rates and exchange market efficiency». Journal of Financial Economics 5 (1): 55–65. DOI:10.1016/0304-405X(77)90029-0. Проверено 2011-06-28.

ru.wikiyy.com

Смотрите также

.