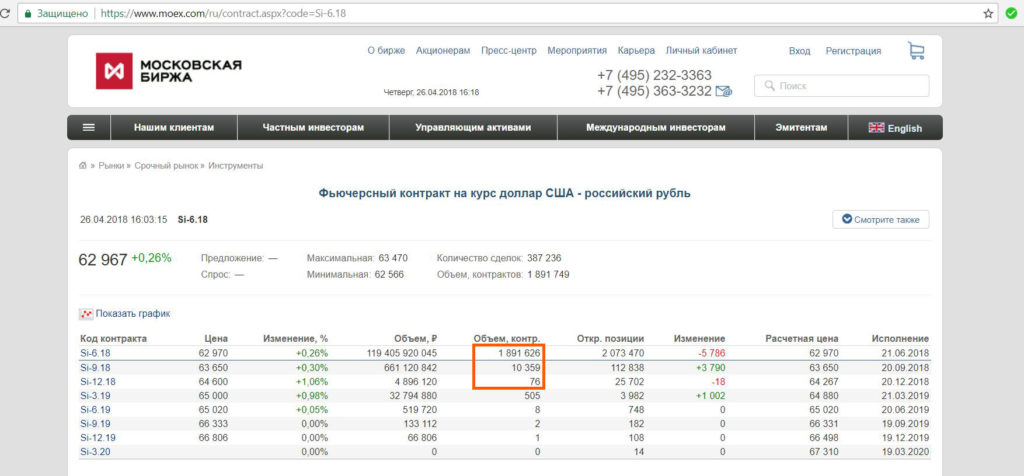
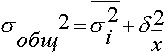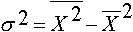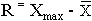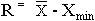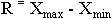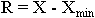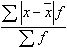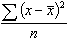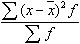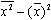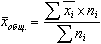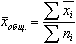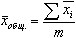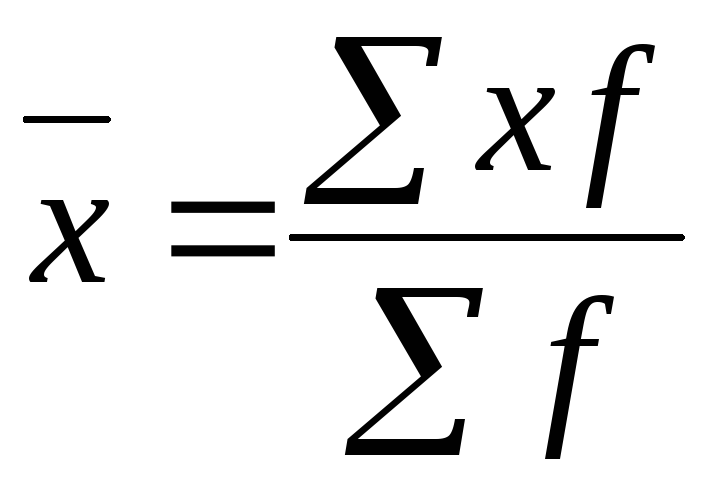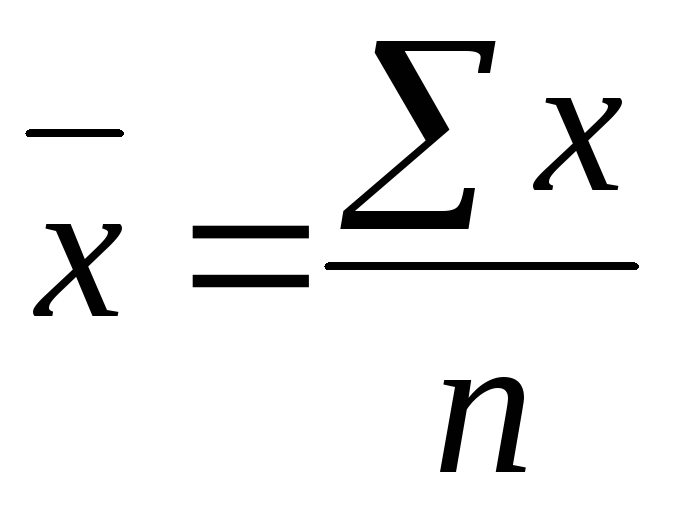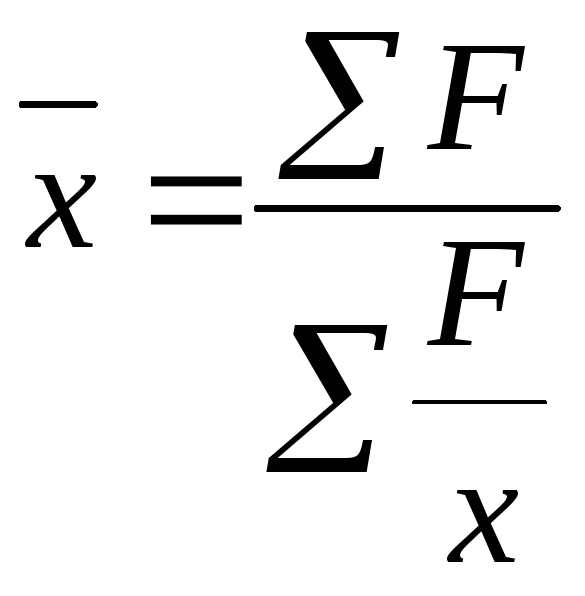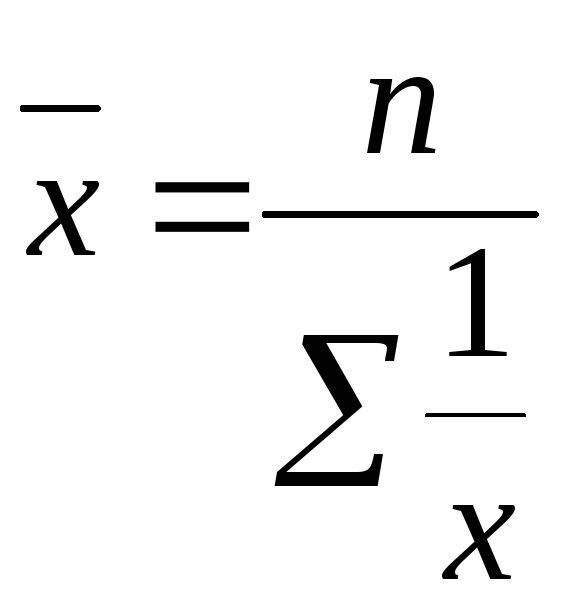Статистика биржевой деятельности и финансового рынка. Средний курс продажи одной акции по данным о торгах на фондовой бирже
14.Вид ряда распределения - ......
| Тарифный разряд рабочих | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
дискретный
интервальный
моментный
15. Средний тарифный разрядрабочих = ...... (с точностью до 0,1) при условии:
| Тарифный разряд рабочих | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
16. Мода в ряду распределения = ...... :
| Тарифный разряд рабочих | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
17. Медиана в ряду распределения = ......:
| Тарифный разряд рабочих | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
18. Абсолютные показатели вариации:
размах вариации
коэффициент корреляции
коэффициент осцилляции
среднее линейное отклонение
среднее квадратическое отклонение
дисперсия
коэффициент вариации.
19. Медиана на основе данных о результатах экзамена по статистике =…
| Балл оценки знаний студентов | 2 (неудовлетворительно) | 3 (удовлетворительно) | 4 (хорошо) | 5 (отлично) |
| Число студентов | 9 | 12 | 24 | 15 |
20. Правило сложения дисперсий выражено формулой:
21. Размах вариации:
22.
Средний курс продажи одной акции по данным о торгах на фондовой бирже ( с точностью до 1 руб.) = …руб. при условии:
| Сделка | Количество проданных акций, шт. | Курс продажи, руб. |
| 1 | 500 | 108 |
| 2 | 300 | 102 |
| 3 | 10 | 110 |
23. Формулы для расчета дисперсии:
24. Если модальное значение признака больше средней величины признака, то это свидетельствует о ...... .
правосторонней асимметрии в данном ряду распределения
левосторонней асимметрии в данном ряду распределения
нормальном законе распределения
биномиальном законе распределения
симметричности распределения
25. Относятся к относительным показателям вариации:
размах вариации
дисперсия
коэффициент вариации
среднее линейное отклонение
относительное линейное отклонение
26.Средняя величина признака равна 22, а дисперсия признака - 36.
Коэффициент вариации= ...... (с точностью до 0,1 %)
27.

28. Значение моды определяется на основе графика ......
кривой Лоренца
полигона распределения
функции распределения
кумуляты
огивы
29. Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300,
на I/V - 2002 г. - 320,
на I/VI - 2002 г. - 310,
на I/VII - 2002 г. – 290
Cредний остаток оборотных средств (с точностью до 0,1 млн.руб.) за 2 квартал = ...... млн. руб.
305
310
308,3
312,5
30. Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300,
на I/V - 2002 г. - 320,
на I/VI - 2002 г. - 310,
на I/VII - 2002 г. – 290
для расчета среднего остатка оборотных средств за 2 квартал следует применить среднюю...... .
гармоническую
геометрическую
хронологическую
степенную
арифметическую
31. Средний уровень издержек обращения на 100 руб. товарооборота ( с точностью до 0,1 руб.) = …руб., при условии:
| Издержки обращения на 100 руб. товарооборота | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| 2-4 | 4 | 75 |
| 4-6 | 6 | 70 |
32. Средний размер товарооборота в расчете на одно предприятие ( с точностью до 1 млн. руб.) = …млн.руб., при условии:
| Издержки обращения на 100 руб. товарооборота | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| 2-4 | 4 | 75 |
| 4-6 | 6 | 70 |
33. Модапо данным о распределении работников предприятия по количеству вырабатываемых деталей за смену равно …..штук:
| Группы работников по количеству вырабатываемых деталей за смену, шт. | Число работников |
| 5800 | 30 |
| 6000 | 45 |
| 6200 | 80 |
| 6400 | 60 |
| 6600 | 35 |
| Итого | 250 |
34. Медианапо данным о распределении работников предприятия по количеству вырабатываемых деталей за смену равно …..штук:
| Группы работников по количеству вырабатываемых деталей за смену, шт. | Число работников |
| 5800 | 25 |
| 6000 | 35 |
| 6200 | 50 |
| 6400 | 48 |
| 6600 | 42 |
| Итого | 200 |
studfiles.net
Выборочное содержание тестовых материалов
52
Уникальный идентификатор НТЗ: ID = 87311636
Наименование НТЗ: Статистика
Расположение НТЗ: D:\Documents and Settings\Статистика\Мои документы\Давыденко НГ\КГАУ\ТЕСТИРОВАНИЕ\Тесты\060400_Финансы и кредит\Статистика.ast
Авторский коллектив НТЗ: Финансовая академия
Дата создания НТЗ: 01.11.2002
Дата конвертации НТЗ: 03.09.2003
Раздел 1. Общая теория статистики
Тема 1. Статистическое наблюдение. Сводка и группировка статистических материалов. Абсолютные и относительные величины
1. Задание {{ 2 }} ТЗ-1-2.
Абсолютные величины могут выражаться в ... .
натуральных единицах измерения
процентах
условно-натуральных единицах измерения
денежных единицах измерения
виде простого кратного отношения
трудовых единицах измерения
2. Задание {{ 3 }} ТЗ-1-3.
Относительные статистические величины могут выражаться в ... .
виде простого кратного отношения
процентах
промилле
трудовых единицах измерения
условно-натуральных единицах измерения
3. Задание {{ 5 }} ТЗ-1-5.
В 1999 г. предприятие увеличило выпуск продукции по сравнению с 1998 г. на 10%, а в 2000 г. выпуск продукции на предприятии по сравнению с 1999 г. снизился на 5%.
Выпуск продукции в 2000 г. по сравнению с 1998 г. составил ... % (с точностью до 0,1 %).
Правильные варианты ответа: 104,5; 104.5;
4. Задание {{ 6 }} ТЗ-1-6.
Графическое изображениеряда:
Группы квартир по размеру
общей площади, кв.м 20-30 30-40 40-50 50-60 60-70
Число квартир, тыс. ед. 10 35 30 15 5
называется ...
гистограмма
полигон распределения
кумулята распределения
плотность распределения
функция распределения
5. Задание {{ 7 }} ТЗ-1-7.
Установите соответствие между видами относительных величин
| доля занятых в общей численности экономически активного населения | относительная величина структуры |
| потребление продуктов питания в расчете на душу населения | относительная величина уровня экономического развития |
| соотношение численности мужчин и женщин в общей численности безработных | относительная величина координации |
| число родившихся на 1000 человек населения | относительная величина интенсивности |
| относительная величина планового задания |
6. Задание {{ 8 }} тз-1-8.
Установите соответствие между видами относительных величин
| доля мужчин в общей численности безработных | относительная величина структуры |
| потребление молока в расчете на душу населения | относительная величина уровня экономического развития |
| соотношение численности мужчин и женщин в общей численности населения | относительная величина координации |
| число умерших на 1000 человек населения | относительная величина интенсивности |
| относительная величина динамики |
7. Задание {{ 9 }} тз-1-9.
Взаимосвязь относительных величин динамики (ОВД), планового задания (ОВПЗ) и выполнения плана (ОВВП) выражается соотношением:
ОВД = ОВПЗ ОВВП
ОВД = ОВПЗ : ОВВП
ОВПЗ = ОВД ОВВП
ОВВП = ОВД ОВПЗ
8. Задание {{ 10 }} ТЗ-1-10.
Сплошному статистическому наблюдению присущи ошибки:
случайные ошибки репрезентативности
случайные ошибки регистрации
систематические ошибки регистрации
систематические ошибки репрезентативности
9. Задание {{ 12 }} ТЗ-1-12.
Cпособы статистического наблюдения :
непосредственное наблюдение
отчетность
опрос
документальную запись
специально организованное наблюдение
10. Задание {{ 13 }} ТЗ-1-13.
Организационные формы статистического наблюдения:
отчетность
непосредственное наблюдение
специально организованное наблюдение
регистр
выборочное наблюдение
11. Задание {{ 14 }} ТЗ-1-14.
Виды несплошного статистического наблюдения:
выборочное наблюдение
обследование основного массива
монографическое
текущее статистическое наблюдение
специально организованное наблюдение
12. Задание {{ 16 }} ТЗ-1-16.
Объединение выполнило план производства на 104 %. По сравнению с прошлым годом прирост выпуска продукции по объединению составил 7 %. Относительная величина планового задания (с точностью до 0,1 %) равна ... .
Правильные варианты ответа: 102,9; 102.9;
13. Задание {{ 17 }} ТЗ-1-17.
Плановый прирост выпуска продукции в текущем году по отрасли должен был составить 6,7 %. Если фактический прирост выпуска продукции по сравнению с базисным годом составил 9,2 %, то степень выполнения плана (процентах с точностью до 0,1%) равна ... %.
Правильные варианты ответа: 102,3; 102.3;
14. Задание {{ 18 }} ТЗ-1-18.
Дискретные признаки группировок:
заработная плата работающих
численность работников предприятий
размер обуви
численность населения стран
разряд сложности работы
число членов семей
15. Задание {{ 19 }} ТЗ-1-19.
Непрерывные признаки группировок:
заработная плата работающих
численность работников предприятий
размер обуви
численность населения стран
разряд сложности работы
число членов семей
16. Задание {{ 20 }} ТЗ-1-20.
Количественные признаки группировок:
прибыль предприятия
пол человека
национальность
возраст человека
посевная площадь
17. Задание {{ 21 }} ТЗ-1-21.
Атрибутивные признаки группировок:
пол человека
национальность
возраст человека
посевная площадь
заработная плата
18. Задание {{ 322 }} ТЗ № 322
Последовательность этапов статистического исследования
1: определение статистической совокупности
2: сбор первичной статистической информации
3: сводка и группировка первичной информации
4: анализ статистической информации
5: рекомендации на основе анализа данных
Тема 2. Средние величины и показатели вариации
1. Задание {{ 22 }} ТЗ-1-22.
Показатели структуры вариационного ряда :
простая средняя арифметическая
мода
медиана
дисперсия
дециль
квартиль
2. Задание {{ 23 }} ТЗ-1-23.
При увеличении всех значений признака в 2 раза средняя величина признака ... .
не изменится
увеличится в 2 раза
уменьшится в 2 раза
увеличится более чем в 2 раза
уменьшится более чем в 2 раза
3. Задание {{ 24 }} ТЗ-1-24.
При уменьшении значений частот в средней арифметической взвешенной в 2 раза значение средней величины признака ... .
не изменится
увеличится в 2 раза
уменьшится в 2 раза
увеличится более чем в 2 раза
уменьшится более чем в 2 раза
4. Задание {{ 26 }} ТЗ-1-26.
Модой называется ... .
среднее значение признака в данном ряду распределения
наиболее часто встречающееся значение признака в данном ряду
значение признака, делящее данную совокупность на две равные части
наиболее редко встречающееся значение признака в данном ряду
серединное значение признака в данном ряду распределения
5. Задание {{ 27 }} ТЗ-1-27.
Соответствие между видом средней величины и ее формулой:
| средняя арифметическая взвешенная | |
| простая средняя арифметическая | |
| средняя гармоническая взвешенная | |
| простая средняя гармоническая | |
6. Задание {{ 28 }} ТЗ-1-28.
Сумма отклонений индивидуальных значений признака от их средней величины ... .
больше нуля
меньше нуля
равна нулю
больше или равна нулю
меньше или равна нулю
7. Задание {{ 29 }} ТЗ-1-29.
Формулы для расчета дисперсии признака:
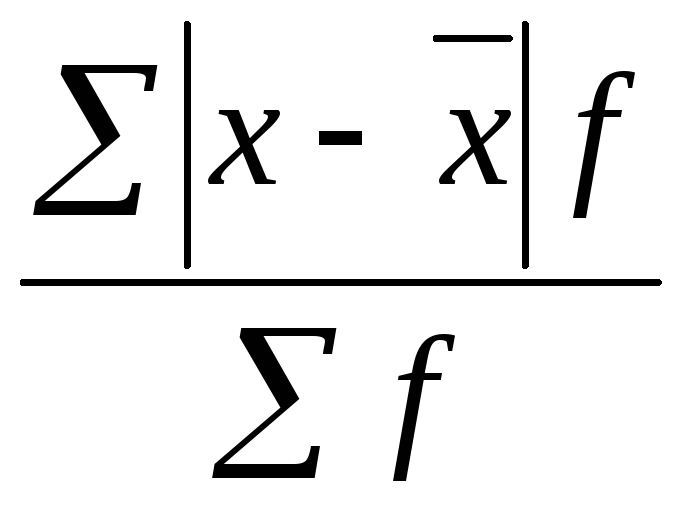
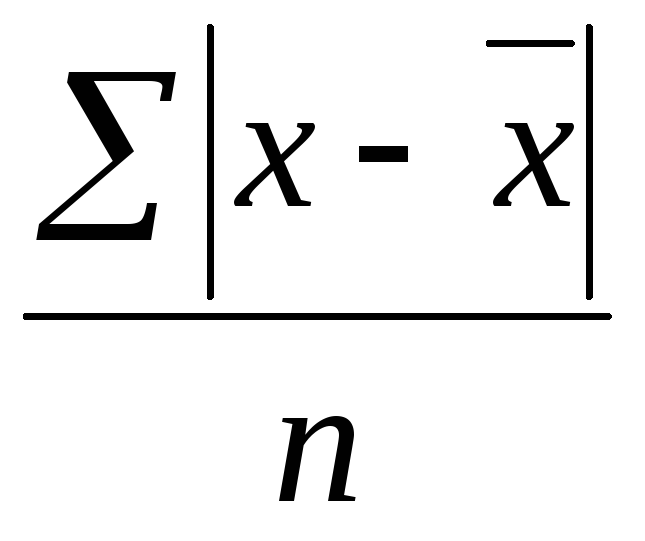
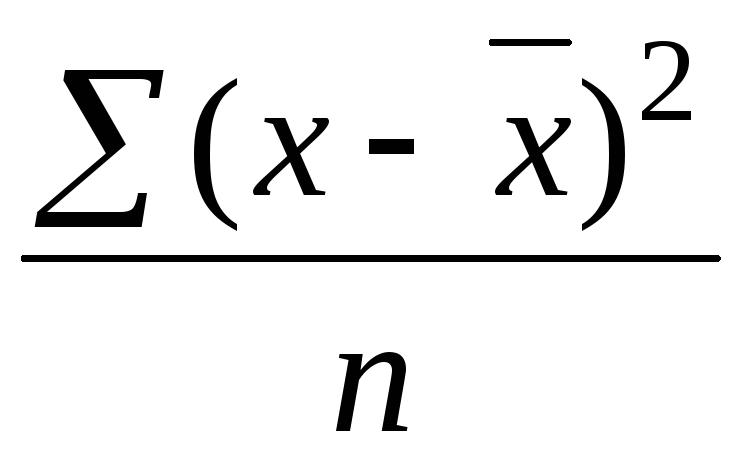
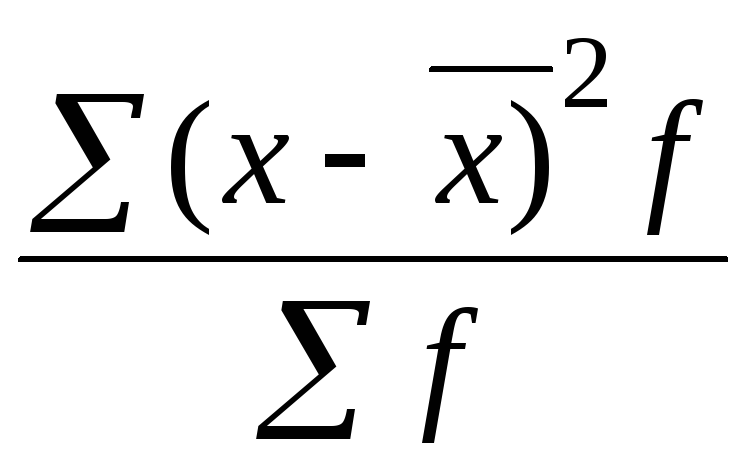
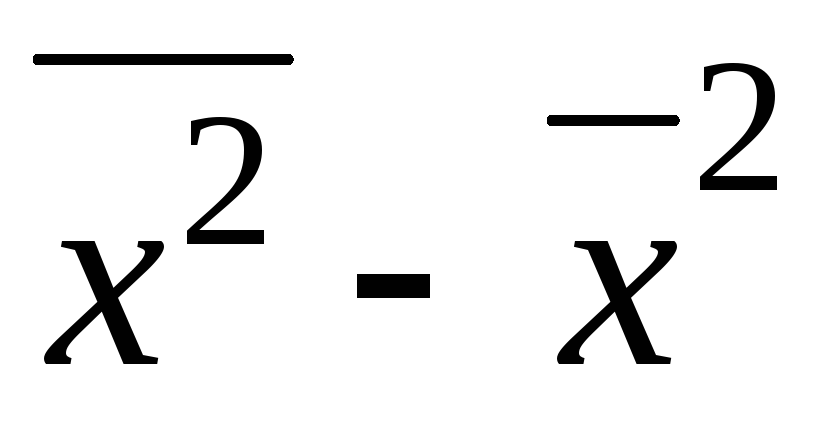
8. Задание {{ 30 }} ТЗ-1-30.
меньше нуля
равна нулю
больше или равна нулю
меньше или равна нулю
7. Задание {{ 29 }} ТЗ-1-29.
Формулы для расчета дисперсии признака:
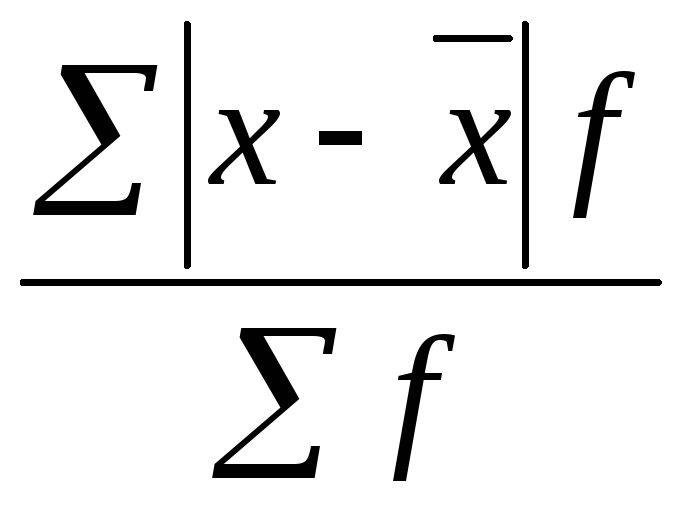
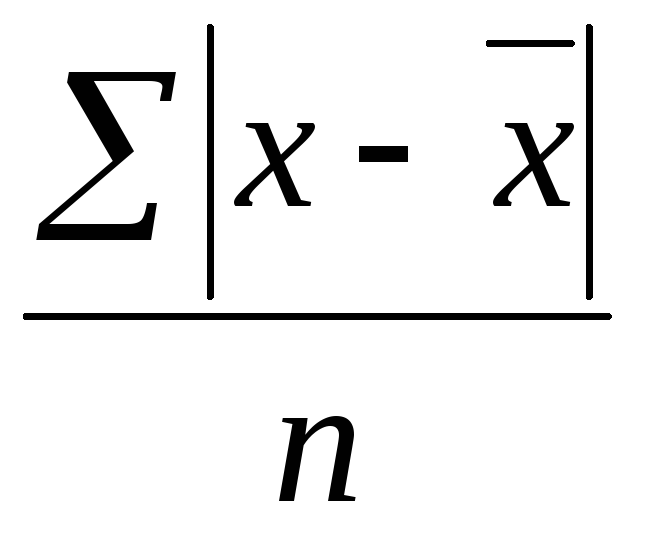
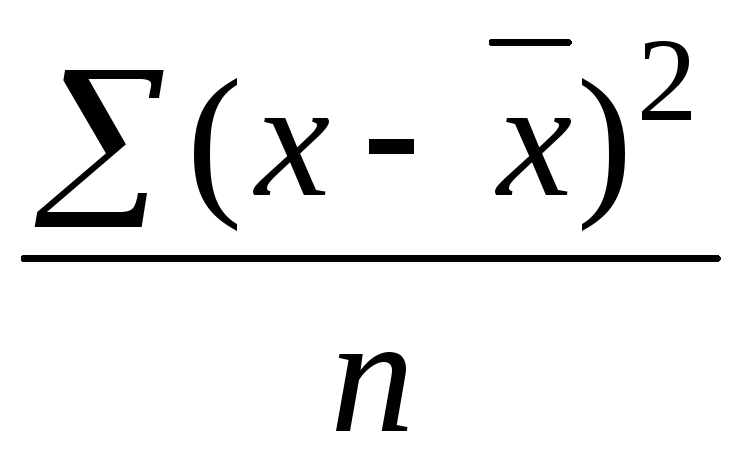
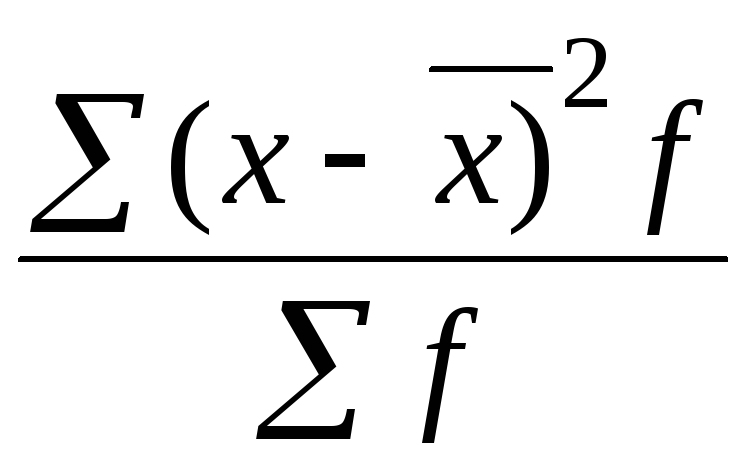
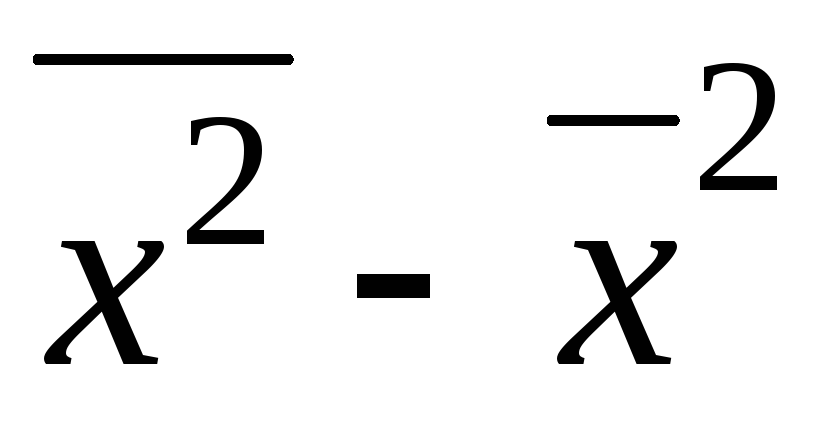
8. Задание {{ 30 }} ТЗ-1-30.
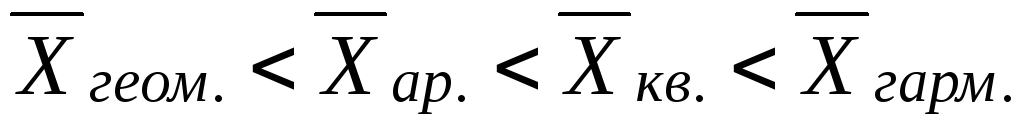
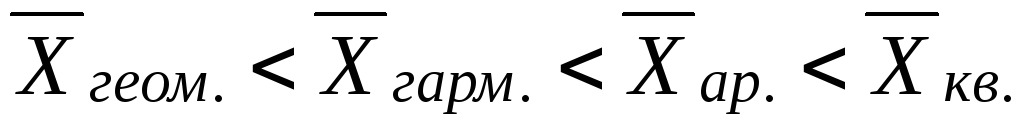
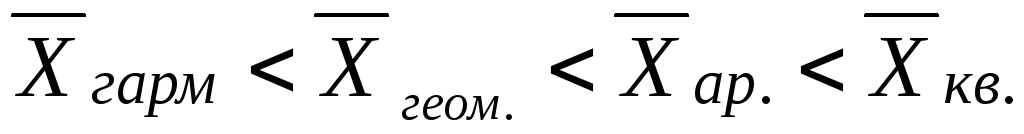
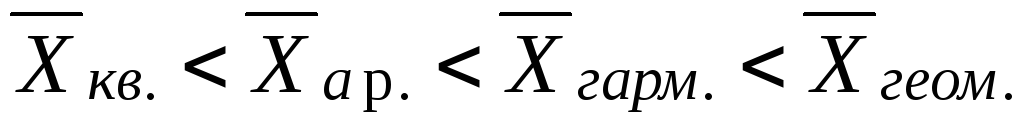
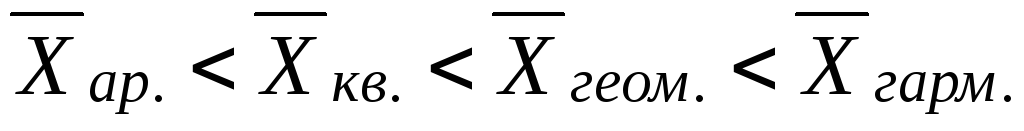
9. Задание {{ 31 }} ТЗ-1-31.
Средняя величина признака равна 20, коэффициент вариации -25 %.
Дисперсия признака равна ... .
Правильные варианты ответа: 25;
10. Задание {{ 32 }} ТЗ-1-32.
Медианой называется ... .
среднее значение признака в ряду распределения
наиболее часто встречающееся значение признака в данном ряду
значение признака, делящее совокупность на две равные части
наиболее редко встречающееся значение признака в данном ряду
значения признака, делящие совокупность на четыре равные части
11. Задание {{ 33 }} ТЗ-1-33.
Средняя величина признака равна 22,
коэффициент вариации признака - 26 %.
Дисперсия признака (с точностью до 0,0001) равна ... .
Правильные варианты ответа: 32,7184; 32.7184;
12. Задание {{ 34 }} ТЗ-1-34.
По ряду распределения:
Группы семей по размеру жилой
площади, приходящейся на 3-5 5-7 7-9 9-11 11-13
одного человека, кв.м
Число семей с данным размером
жилой площади 10 21 28 30 26
Мода (с точностью до 0.1) равна …
Правильные варианты ответа: 9,7; 9.7;
13. Задание {{ 35 }} ТЗ-1-34.
Ряд распределения:
| Группы семей по размеру жилой площади, приходящейся на одного человека, кв.м. | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число семей с данным размером жилой площади | 10 | 21 | 28 | 30 | 26 |
Медиана (с точностью до 0.1) равна …
Правильные варианты ответа: 8,9; 8.9;
14. Задание {{ 37 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Cредний тарифный разряд рабочих равен ... (с точностью до 0,1).
Правильные варианты ответа: 3,9; 3.9;
15. Задание {{ 38 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Мода равна ... (с точностью до 0,1).
Правильные варианты ответа: 4; 4,0; 4.0;
16. Задание {{ 39 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Медиана равна ... (с точностью до 0,1).
Правильные варианты ответа: 4; 4,0; 4.0;
17. Задание {{ 40 }} ТЗ-1-36.
Абсолютные показатели вариации:
размах вариации
коэффициент корреляции
коэффициент осциляции
среднее линейное отклонение
дисперсия
18. Задание {{ 41 }} ТЗ-1-37.
Результат экзамена по статистике :
| Балл оценки знаний студентов | 2 (неудовлетво рительно) | 3 (удовлетво рительно) | 4 (хорошо) | 5 (отлично) |
| Число студентов | 9 | 12 | 24 | 15 |
Медиана равна …
Правильные варианты ответа: 4; хорошо;
19. Задание {{ 42 }} ТЗ-1-38.
Правило сложения дисперсий выражается формулой ... .
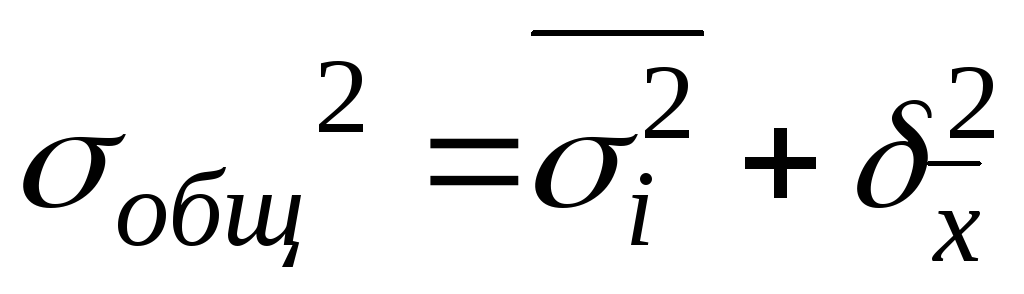
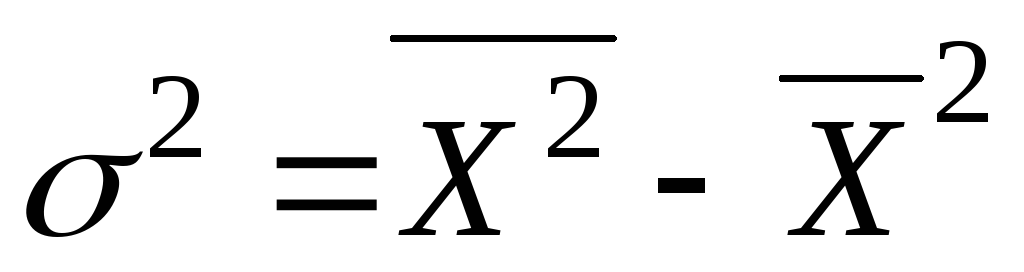
20. Задание {{ 43 }} ТЗ-1-39.
Размах вариации - это ... .
R = Хmax - 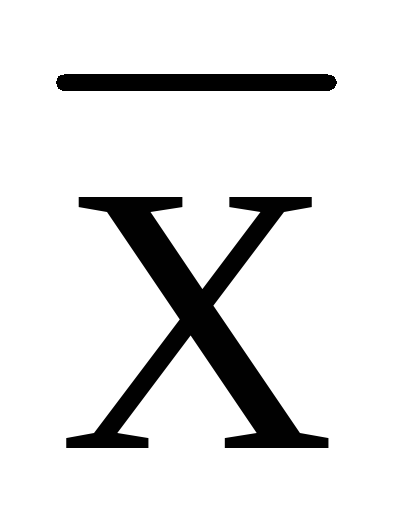
R =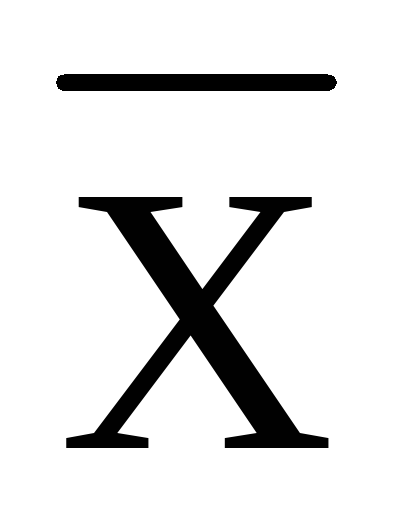 - Хmin
- Хmin
R = Хmax - Хmin
R = Х - Хmin
21. Задание {{ 44 }} ТЗ-1-40.
Данные о торгах на фондовой бирже :
| Сделка | Количество проданных акций, шт. | Курс продажи, руб. |
| 1 2 3 | 500 300 10 | 108 10 1000 |
Средний курс продажи одной акции (с точностью до целых) равен …
Правильные варианты ответа: 83;
22. Задание {{ 45 }} ТЗ-1-41.
Дисперсия рассчитывается как ... .
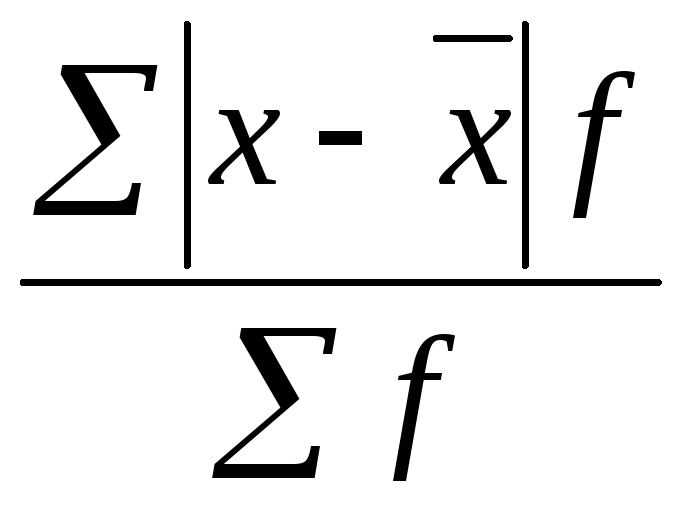
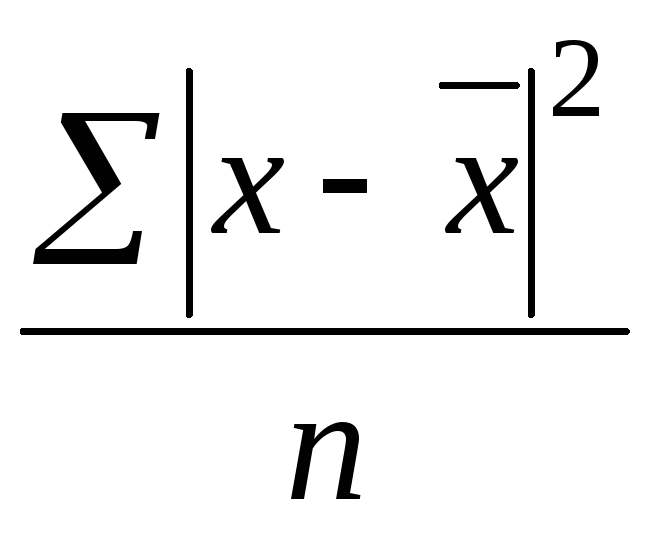
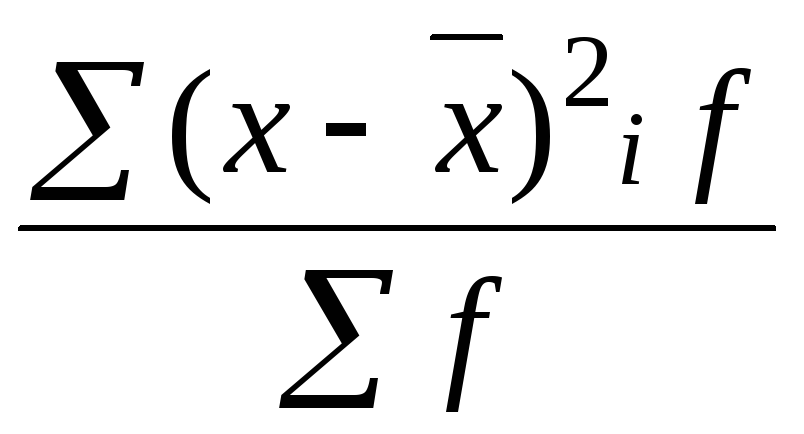
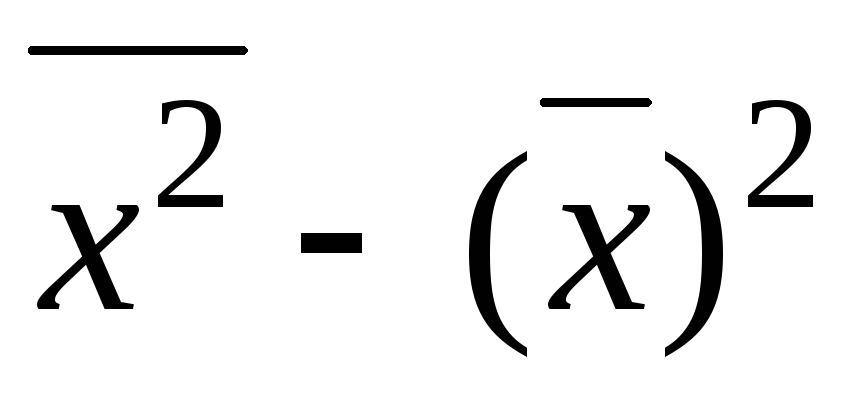
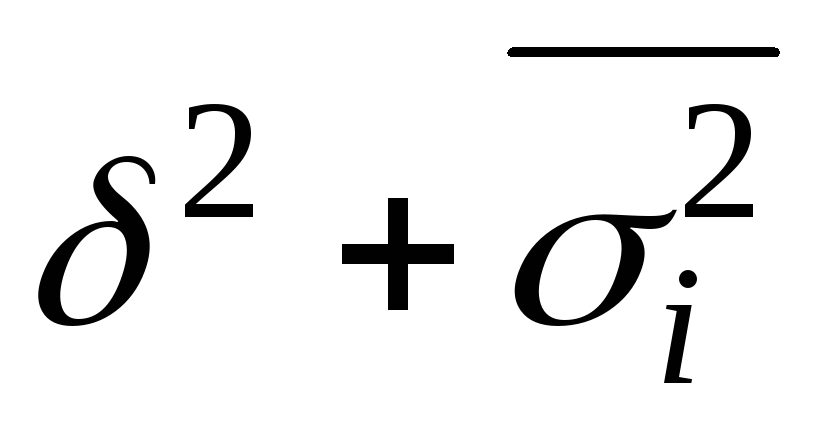
23. Задание {{ 46 }} ТЗ-1-42.
Если модальное значение признака больше средней величины признака, то это свидетельствует о ... .
правосторонней асимметрии в данном ряду распределения
левосторонней асимметрии в данном ряду распределения
симметричности распределения;
нормальном законе распределения
биномиальном законе распределения
24. Задание {{ 47 }} ТЗ-1-43.
Относительные показатели вариации :
размах вариации
дисперсия
коэффициент вариации
среднее линейное отклонение
относительное линейное отклонение
25. Задание {{ 48 }} ТЗ-1-44.
Средняя величина признака равна 22,
дисперсия признака - 36.
Коэффициент вариации равен ... (с точностью до 0,1 %).
Правильные варианты ответа: 27,3; 27.3;
26. Задание {{ 49 }} ТЗ-1-45.
Статистическая совокупность разбита на m групп по факторному признаку. В каждой группе исчислено среднее значение результативного признака:
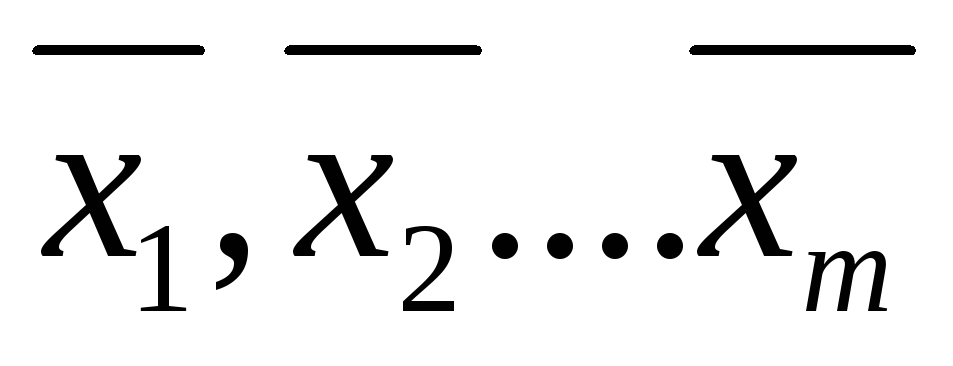 ,
,
численность единиц в каждой группе n1, n2, …,nm.
Среднее значение в целом по совокупности определяется как :
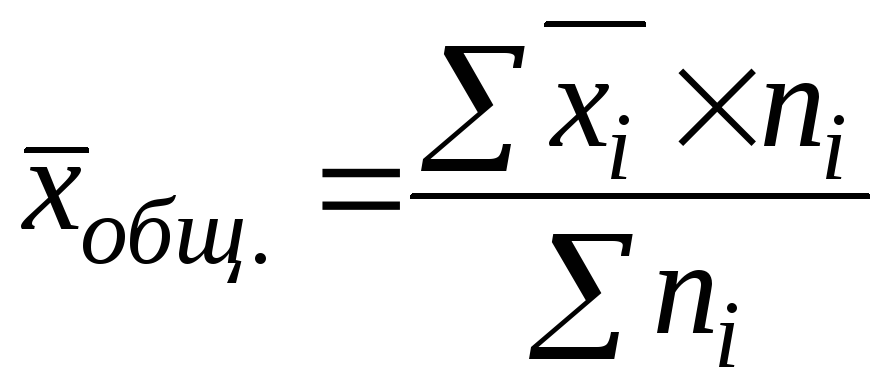
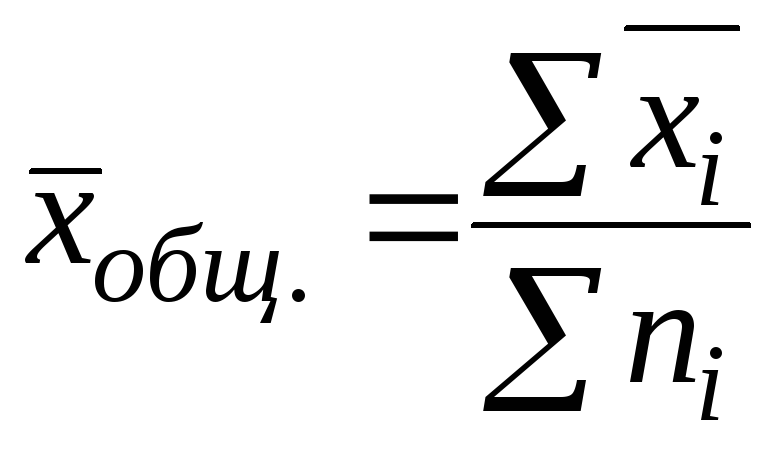
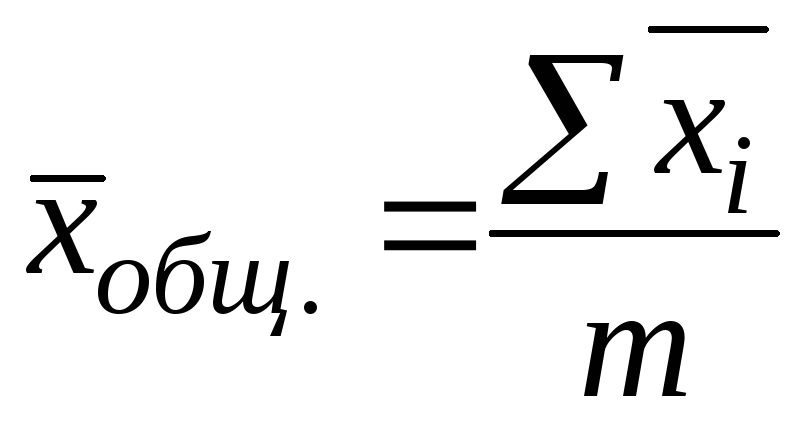
27. Задание {{ 50 }} ТЗ-1-46.
Значение моды определяется на основе графика ... .
полигона распределения
функции распределения
кумуляты
огивы
кривой Лоренца
28. Задание {{ 51 }} ТЗ-1-47.
Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300
на I/V - 2002 г. - 320
на I/VI - 2002 г. - 310
на I/VII - 2002 г. - 290
Cредний остаток оборотных средств (с точностью до 0,1 млн.руб.) за 2 квартал равен ... млн. руб.
305
310
308,3
312,5
29. Задание {{ 52 }} ТЗ-1-48.
Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300
на I/V - 2002 г. - 320
на I/VI - 2002 г. - 310
на I/VII - 2002 г. - 290
для расчета среднего остатка оборотных средств за 2 квартал следует применить среднюю... .
гармоническую
геометрическую
хронологическую
степенную
арифметическую
30. Задание {{ 53 }} ТЗ-1-49
Средний уровень издержек обращения на 100 руб. товарооборота по данным(с точностью до 0,1 руб.)
| Издержки обращения на 100 руб. товарооборота, руб. | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| до 2 2 - 4 4 - 6 6 и выше | 4 6 10 12 | 75 70 67 60 |
равен …
Правильные варианты ответа: 4,7; 4.7;
31. Задание {{ 54 }} ТЗ-1-50.
Средний размер товарооборота на одно предприятие по данным:
| Издержки обращения на 100 руб. товарооборота, руб. | Число предприятий | Товарооборот в среднем на одно предприятие, млн. руб. |
| до 2 2 - 4 4 - 6 6 и выше | 4 6 10 12 | 75 70 67 60 |
равен (с точностью до 0,1 млн. руб.) …
Правильные варианты ответа: 65,9; 65.9;
32. Задание {{ 55 }} ТЗ-1-51.
Данные о распределении работников предприятия по размеру месячной заработной платы:
| Группы работников по размеру заработной платы, руб. | Число работников |
| 800 1000 1200 1400 1600 | 30 45 80 60 35 |
Мода равна …
Правильные варианты ответа: 1200;
33. Задание {{ 56 }} ТЗ-1-52.
Данные о распределении работников предприятия по размеру месячной заработной платы :
| Группы работников по размеру заработной платы, руб. | Число работников |
| 800 1000 1200 1400 1600 | 30 45 80 60 35 |
Медиана равна …
Правильные варианты ответа: 1200;
34. Задание {{ 58 }} ТЗ-1-54.
Для значений признака: 3, 5, 6, 9, 11, 12, 13
Мода ... .
отсутствует
равна 3
равна 13
равна 9
равна 6
35. Задание {{ 59 }} ТЗ-1-55.
Для значений признака: 3, 3, 3, 4, 4, 6, 7, 9, 9
Мода ... .
равна 6
отсутствует
равна 3
равна 4
равна 9
36. Задание {{ 60 }} ТЗ-1-56.
Средний квадрат индивидуальных значений признака равен 625,
дисперсия - 400.
Величина средней равна ... .
Правильные варианты ответа: 15;
37. Задание {{ 62 }} ТЗ-1-58.
При осмотре партии деталей среди них оказалось 10 бракованных изделий.
Если в полученной партии было 200 изделий, то дисперсия равна ... .
Правильные варианты ответа: 0,0475; 0.0475;
38. Задание {{ 323 }} ТЗ № 323
Дисперсия альтернативного признака ...
0,5 < 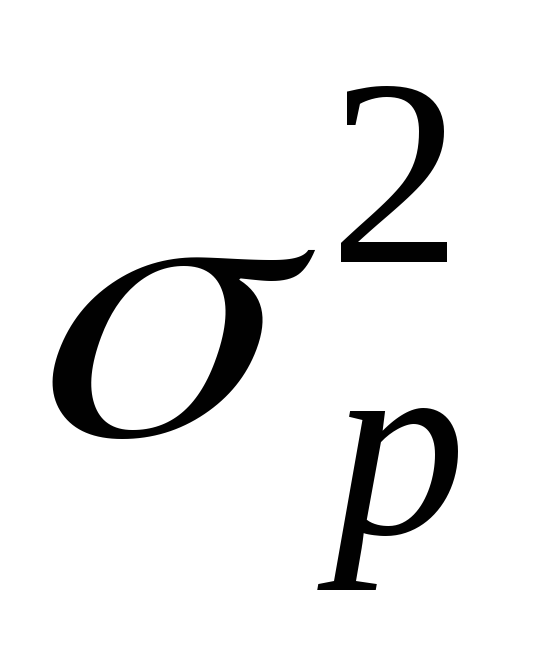 1
1
0 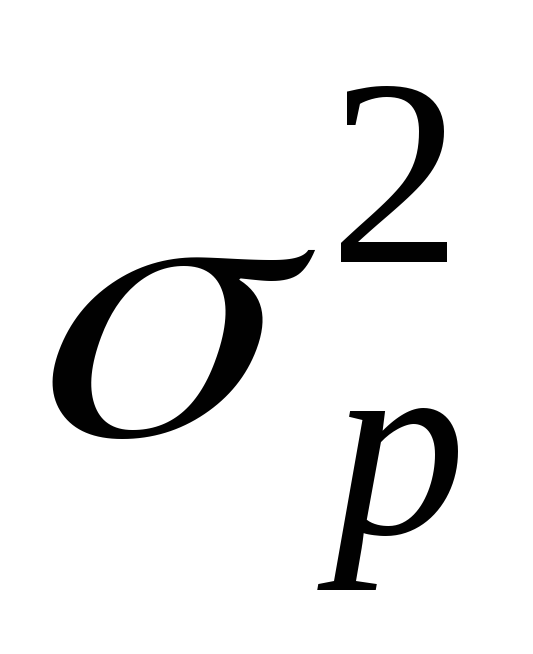
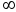
0 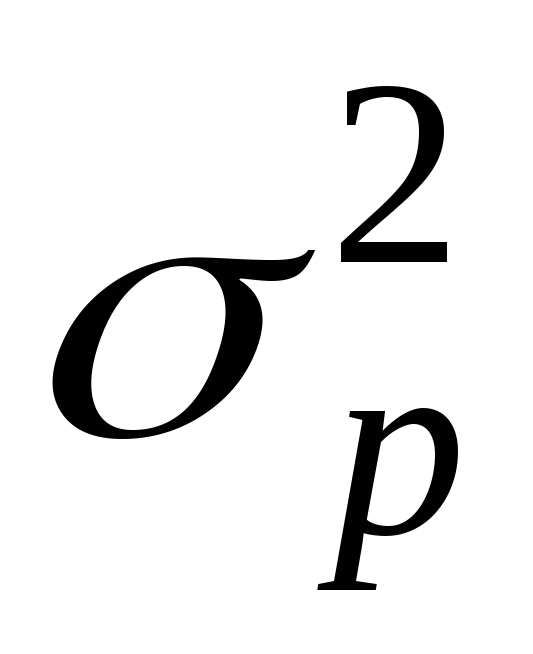 0,25
0,25
0,25 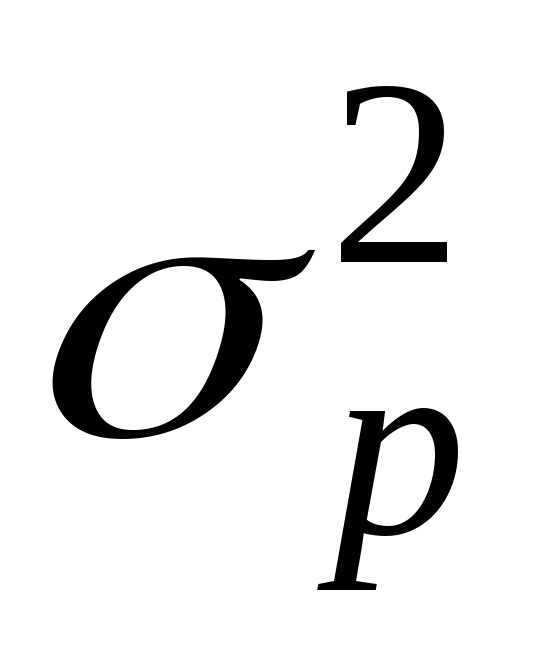 1
1
Тема 3. Индексы
1. Задание {{ 63 }} ТЗ-1-59.
Стоимость реализованной продукции за текущий период увеличилась на 15%.
Цены на продукцию за этот период также увеличились на 15%.
Количество реализованной продукции ... .
увеличилось на 32%
уменьшилось на 5%
уменьшилось на 32 %
увеличилось на 5 %
не изменилось
2. Задание {{ 64 }} ТЗ-1-60.
Количество реализованной продукции за текущий период увеличилось на 20 %.
Цены на продукцию за этот период также увеличились на 20 %.
Стоимость реализованной продукции ... .
увеличилась на 44 %
уменьшилась на 44 %
уменьшилась на 40 %
увеличилась на 40 %
не изменилась
3. Задание {{ 65 }} ТЗ-1-61.
Стоимость реализованной продукции за текущий период увеличилась на 15%. Количество реализованной продукции за этот период также увеличилось на 15%.
Цены на продукцию ... .
увеличились на 32%
уменьшились на 5%
уменьшились на 32 %
увеличились на 5 %
не изменились
4. Задание {{ 66 }} ТЗ-1-62.
Объем производства продукции на предприятии за год (в стоимостном выражении) увеличился по сравнению с предыдущим годом на 1,3%.
Индекс цен на продукцию составил 105%.
Индекс количества произведенной продукции равен ... (с точностью до 0,1 %).
Правильные варианты ответа: 96,5; 96.5;
5. Задание {{ 67 }} ТЗ-1-63.
Формулы для расчета индекса фиксированного (постоянного) состава:
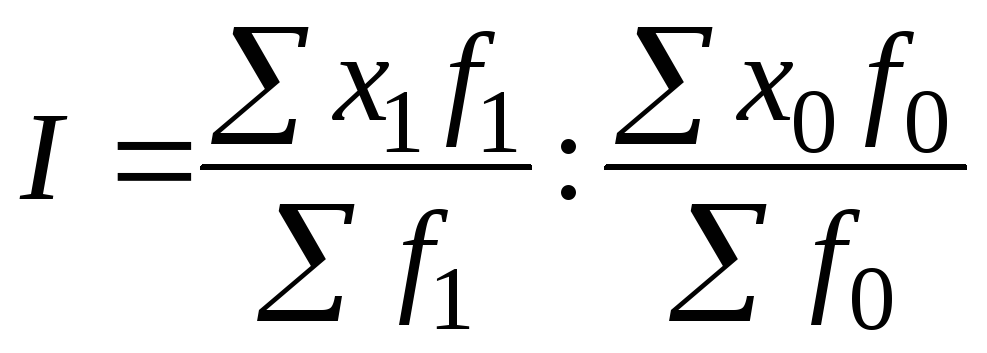
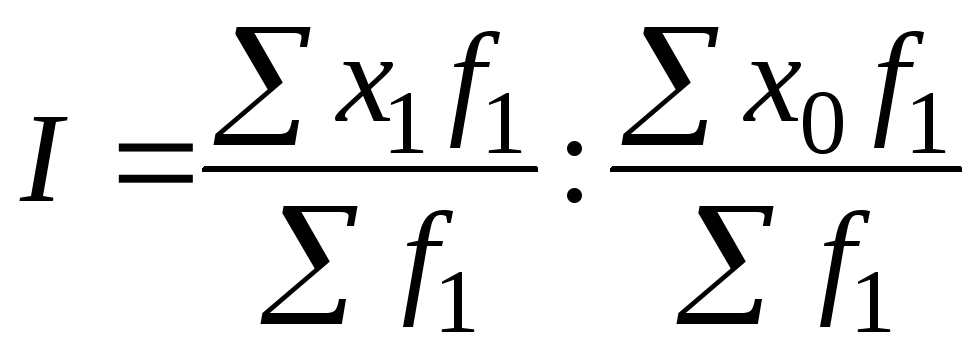
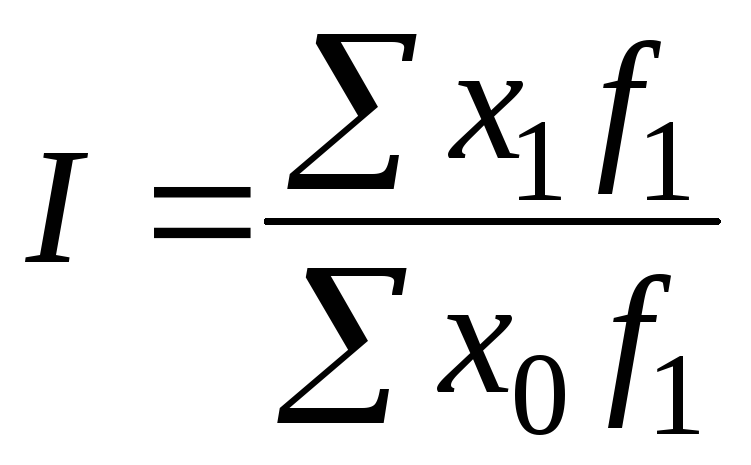
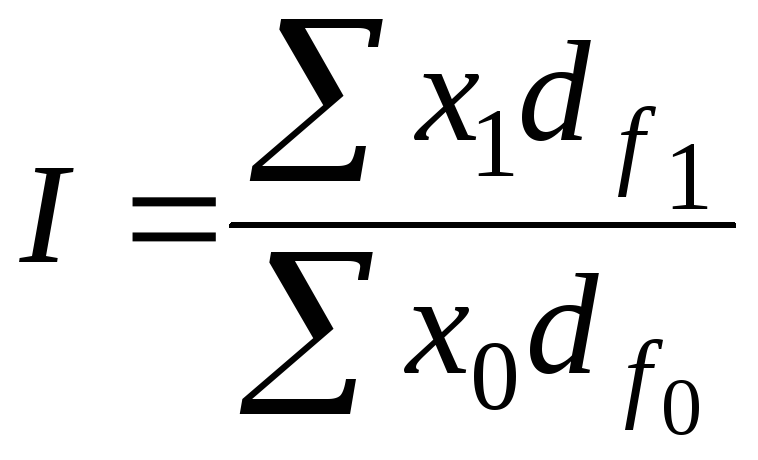 , где
, где 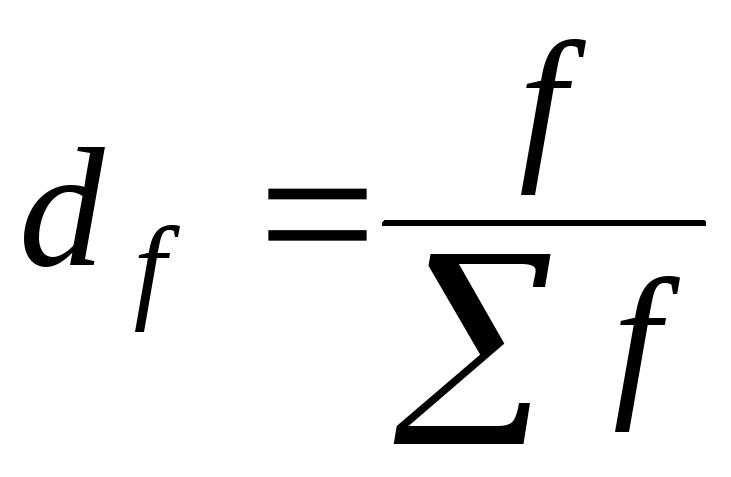
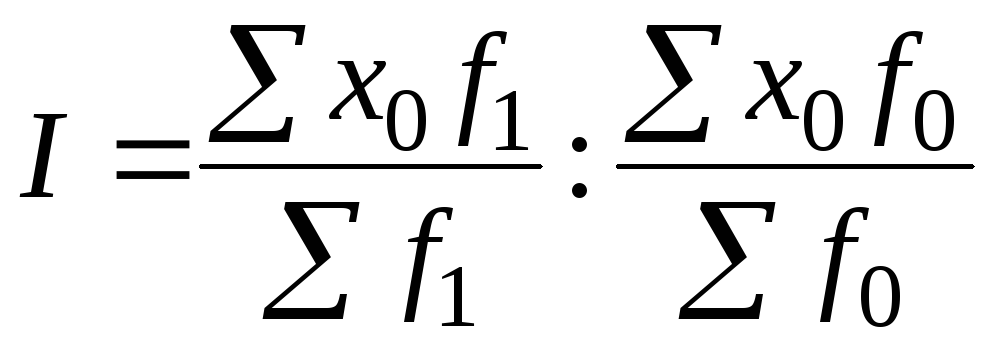
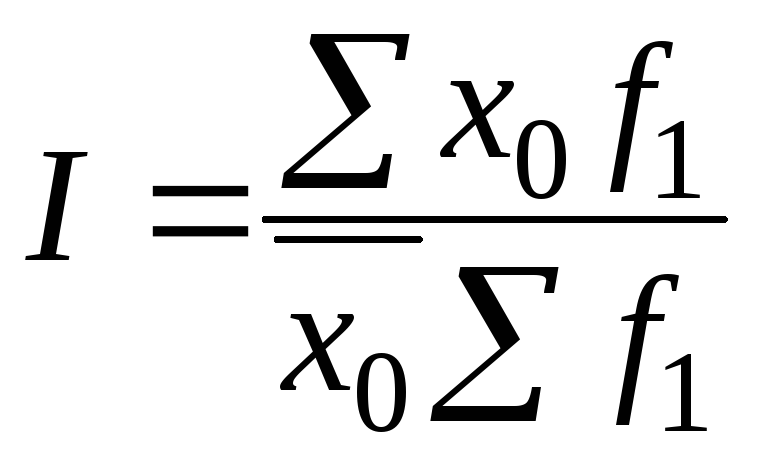
6. Задание {{ 68 }} ТЗ-1-64.
| Виды продукции | Общая сумма затрат на производство продукции, млн. руб. | Изменение себестоимости единицы продукции в отчетном периоде по сравнению с базисным, % | |
| базисный период | отчетный период | ||
| Обувь муж. Обувь жен. | 230 290 | 240 300 | +6,0 -2,0 |
Общий индекс себестоимости продукции (с точностью до 0,1%) равен …
Правильные варианты ответа: 101,4; 101.4;
studfiles.net
Статистика биржевой деятельности и финансового рынка
Задача № 200
Имеются следующие данные по акциям:
| Тип акции | Количество акций, находящихся в обращении, шт. | Рыночная стоимость, руб. | ||
| 200 | 2005 | 2006 | 2005 | |
| 1 | 2 | 3 | 4 | 5 |
| А | 130000 | 120000 | 10 | 13 |
| Б | 100000 | 90000 | 8,5 | 6,2 |
| В | 85000 | 125000 | 15 | 13,5 |
Определите:
1) показатель рыночной капитализации по акциям, котируемым на бирже;
2) изменение рыночной капитализации за год.
Задача № 201
По данным предыдущей задачи определите показатель оборачиваемости по всем видам ценных бумаг, если стоимостный объем бумаг составил, (млн. руб.):
| Тип акций | 2006 год | 2007 год |
| А | 145 | 178 |
| Б | 85 | 120 |
| В | 310 | 300 |
Задача № 202
По нижеследующим данным:
| Тип акции | Цена предложения, руб. | Цена спроса, руб. |
| А | 23,48 | 22,55 |
| Б | 106,18 | 104,39 |
| В | 8,44 | 8,02 |
| Г | 46,32 | 48,88 |
Оценить ликвидность акций.
Задача № 203
По нижеследующим данным:
| Компания | Количество эмитированных акций, шт. | Выручка от реализации, тыс. руб. | Прибыль после налогообложения, тыс. руб. | Цена акции, руб. |
| 1 | 2 | 3 | 4 | 5 |
| А | 1200000 | 25400,0 | 2989,7 | 31,0 |
| Б | 750000 | 300000,0 | 64880,0 | 75,0 |
Определите коэффициенты 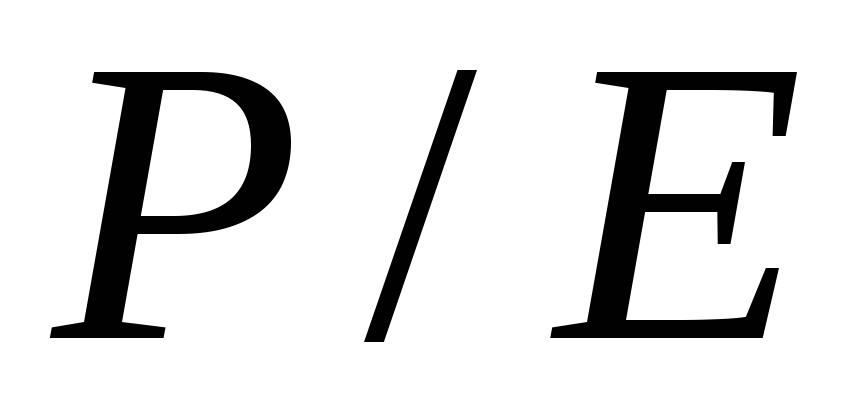 и
и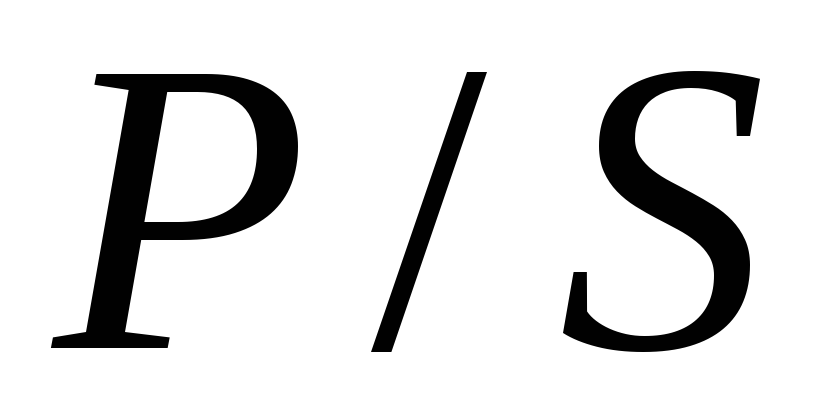 и сделать выводы об оцененности акций.
и сделать выводы об оцененности акций.
Задача № 204
По нижеследующим данным:
| Компания | Цена акции (лот), руб. | Количество акций в лоте, шт. |
| А | 25,70 25,72 25,65 | 20000 15000 100000 |
| Б | 108,77 107,99 108,65 | 5000 7000 10000 |
Определите средневзвешенные цены акций.
Задача № 205
За 1000 акций номиналом 100 руб. инвестор уплатил 125,0 тыс. руб. Дивиденды составляют 10 руб. на акцию. Определите текущую доходность акции.
Задача № 206
Инвестор приобрел 500 акций номиналом 1000 руб. за 600 тыс. руб. Размер дивиденда – 8 % годовых. В настоящее время курсовая стоимость акции – 1100 руб.Определите текущую доходность акции.
Задача № 207
Котировка обыкновенных акций компании – 1200 руб. за акцию. Дивиденд по акции составляет 100 руб. на одну акцию. Определите доходность этих акций.
Задача № 208
Котировка облигации в день выплаты купона составляет 500 руб. Следующий купон будет выплачен через полгода и составит 50 руб. Определите какова годовая текущая доходность облигации.
Задача № 209
Определите текущую доходность облигации номинальной стоимостью 2000 руб., приобретенной по цене 2200 руб., и годовым купоном 20 %.
Задача № 210
Через 90 дней предприятие должно получить по векселю 800000 руб. Предприятие продало этот вексель по простой учетной ставке 15 % годовых (год равен 360 дням). Определите полученную предприятием сумму.
Задача № 211
Вексель на сумму 800000 руб., срок погашения которого наступит через 5 лет, учтен банком по сложной учетной ставке 15 % годовых.
Определите какую сумму получил владелец векселя.
Задача № 212
Исходя из нижеследующих данных по компаниям:
| Акции компаний | Цена акции, руб. | Количество акций, шт. | |
| номинальная | рыночная | ||
| А | 1000 | 1500 | 7000 |
| Б | 100 | 220 | 2000 |
| В | 50 | 45 | 1500 |
Определите:
1) курс акции каждого типа;
2) рыночную стоимость (капитализацию) акций;
3) средний курс акций.
Задача № 213
Исходя из следующих данных:
| Акции компаний | Базисный период | Отчетный период | ||
| количество акций, шт. | цена акции, руб. | количество акций, шт. | цена акции, руб. | |
| А | 475 | 135 | 500 | 150 |
| Б | 800 | 1000 | 720 | 980 |
| В | 250 | 1450 | 250 | 1450 |
Определите фондовый индекс текущего периода, сделайте вывод.
Базовый индекс составлял 100%.
Задача № 214
Имеются данные по акциям, котируемым на бирже:
| Вид акции | Рыночная стоимость, руб. | Количество акций, находящихся в обращении, шт. | ||
| 2006 г. | 2007 г. | 2006 г. | 2007 г. | |
| А | 100 | 150 | 120000 | 110000 |
| Б | 25 | 20 | 80000 | 50000 |
| В | 250 | 300 | 145000 | 170000 |
Определите показатель рыночной капитализации и его изменение за год.
Задача № 215
Биржевой оборот по Российской Федерации характеризуется следующими данными, (млн. руб.):
| Показатель | 2004 г. | 2005 г. | 2006 г. |
| А | 1 | 2 | 3 |
| Биржевой оборот – всего В том числе: | 11596 | 6657 | 6346 |
| Потребительские товары | 6965 | 1646 | 5092 |
| Продукция производственно - технического назначения | 4408 | 4822 | 972 |
| Прочие | 223 | 189 | 282 |
Определите:
1) относительные величины структуры за каждый период;
2) относительные величины динамики.
Задача № 216
Акция номиналом 1000 руб. приобретена за 1500 руб. и продана через год за 2000 руб. Ставка дивиденда равна 20 % годовых, т.е Рн=100 руб.; Рк=2000 руб.; iд= 20%.
Определите:
1) дивиденд;
дополнительный доход;
совокупный доход;
совокупную доходность;
рендит.
Задача № 217
Облигация номиналом 2000 руб. и сроком погашения займа 3 года с ежегодной выплатой дохода по ставке 20 % приобретена с премией за 2900 руб. в первый год после эмиссии и находится у владельца до момента погашения, т.е. Рн=2000 руб.; Рпр=2900 руб; iк=20 % или 0,2.
Определите:
годовой купонный доход;
убыток капитала за весь срок;
годовой убыток капитала;
совокупный доход;
совокупную доходность.
Задача № 218
По нижеследующим данным определите, в какую из перечисленных акций вложения наиболее рискованны:
| Вероятность получения дохода | Ожидаемая ставка доходности, % | ||
| А | Б | В | |
| 0,2 | 80 | 40 | 10 |
| 0,3 | 75 | 44 | 11 |
| 0,4 | 70 | 48 | 12 |
| 0,1 | 65 | 52 | 13 |
Задача № 219
Инвестор имеет возможность сформировать портфель из следующих ценных бумаг (доходность не нормирована):
| Показатели доходности ценных бумаг | Номер ценной бумаги | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Ожидаемая ставка доходности, % | 20 | 22 | 16 | 24 | 12 |
| Среднее квадратическое отклонение, % | 9 | 10 | 16 | 11 | 4 |
Определитепортфель с наибольшим уровнем риска, наименьшим уровнем риска.
Задача № 220
С помощью встроенных статистических функций пакета Excel в среде Windows осуществите расчеты коэффициентов  и
и на базе следующих исходных данных:
на базе следующих исходных данных:
| Период | Доходность по безрисковым активам | Реализованная доходность акций компании | Доходность на базе индекса Standard & Poor, s |
| 1 | 2 | 3 | 4 |
| 1 | 3,90 | - 7,47 | - 5,86 |
| 2 | 4,06 | - 6,54 | - 2,94 |
| 3 | 2,90 | 8,20 | 13,77 |
| 4 | 1,76 | 2,48 | 14,82 |
| 5 | 1,90 | 3,15 | 11,91 |
| 6 | 2,0 | 4,10 | 11,95 |
| 7 | 2,22 | 6,18 | - 0,783 |
| 8 | 2,11 | - 2,15 | 0,02 |
| 9 | 2,16 | 1,54 | - 2,52 |
| 10 | 2,34 | 3,17 | - 1,85 |
| 11 | 2,44 | 2,46 | 8,73 |
| 12 | 2,40 | 7,50 | 1,63 |
| 13 | 1,89 | 6,20 | 10,82 |
| 14 | 1,94 | 1,40 | 7,24 |
| 15 | 1,72 | 1,50 | 6,15 |
| 16 | 1,75 | 3,10 | 14,20 |
| 17 | 1,60 | 2,17 | - 2,08 |
| 18 | 1,94 | 3,15 | 1,06 |
| 19 | 2,07 | - 4,15 | - 4,20 |
| 20 | 2,52 | - 3,10 | - 5,10 |
Задача № 221
По нижеследующим условным исходным данным определите значения агрегатных индексов акций на базе различных типов средних величин (средней арифметической из абсолютных цен; средней арифметической из относительных цен; средней геометрической из относительных цен; средней гармонической из относительных цен; медианы из относительных цен):
| Период | Акции компании, руб. | ||
| А | В | С | |
| 1 | 2 | 3 | 4 |
| 1 | 17,8 | 37,1 | 112,0 |
| 2 | 17,4 | 37,6 | 112,0 |
| 3 | 16,5 | 39,0 | 112,1 |
| 4 | 16,9 | 38,7 | 112,1 |
| 5 | 17,2 | 38,0 | 112,1 |
| 6 | 17,5 | 39,2 | 112,1 |
| 7 | 17,8 | 39,4 | 112,2 |
| 8 | 18,3 | 40,1 | 112,4 |
| 9 | 18,5 | 41,2 | 112,3 |
| 10 | 18,6 | 42,0 | 112,2 |
Задача № 222
Цены акций компании следующие:  – 26 рублей,
– 26 рублей,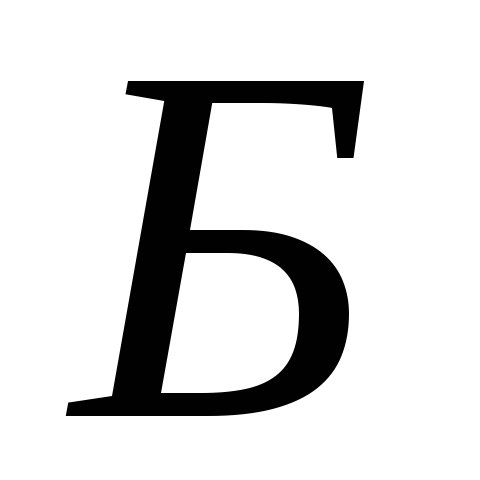 – 35,2 рубля,
– 35,2 рубля, – 28,5 рублей,
– 28,5 рублей,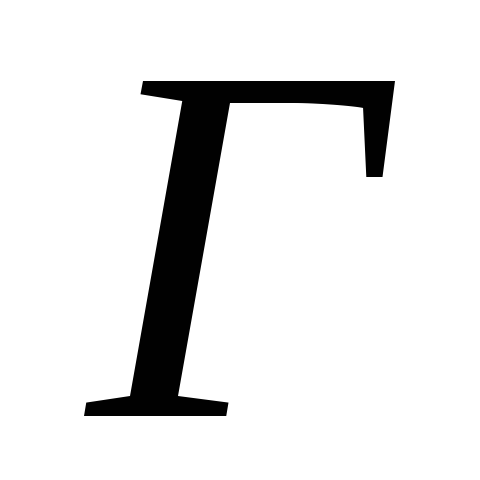 – 20,5 рубля. Из расчета исключаются акции компании В с ценой за акцию 28,5 рубля и добавляются акции компании Д с ценой за акцию 32 рубля.
– 20,5 рубля. Из расчета исключаются акции компании В с ценой за акцию 28,5 рубля и добавляются акции компании Д с ценой за акцию 32 рубля.
Определите поправочный коэффициент 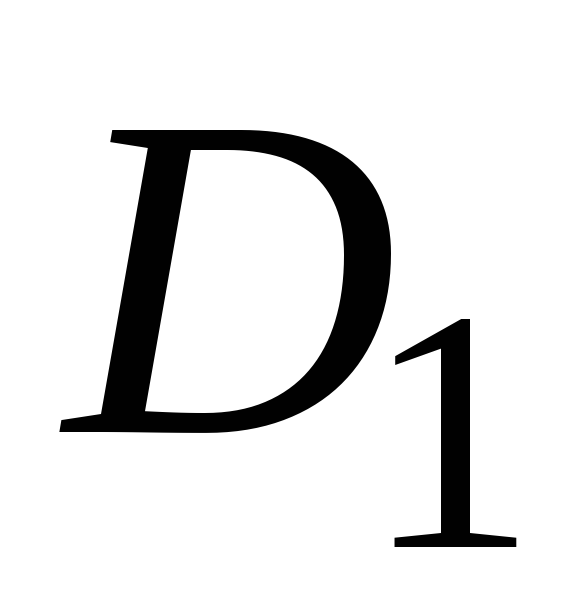 .
.
Задача № 223
Определите кросс – курс английского фунта стерлингов в Ростове – на – Дону и курс швейцарского франка в Стамбуле, если:
- курс доллара в Ростове – на – Дону: 1 $ = 27,8 рубля;
- курс доллара в Лондоне: 1 $ = 0,54 фунта стерлингов;
- курс доллара в Берне: 1 $ = 1,2285 швейцарского франка;
Задача № 224
За апрель 2006 года номинальный валютный курс японской иены к доллару упал с 112,5 до 114,95 иен/долл. Цены за этот же месяц в США выросли на 0,6, а в Японии – на 2,8 %. Определите реальный валютный курс и его динамику.
Задача № 225
На 1 доллар США можно получить 0,79 евро, а за 1 рубль - 27,63 доллара США. Определите кросс – котировку (руб./евро) и (евро/руб.).
Задача № 226
Фунт стерлингов официально снизился с 2,2 до 1,8. Страны – английские экспортеры и импортеры не провели девальвацию одновременно с фунтом стерлингов.
Определите:
процент девальвации фунта стерлингов;
процент вынужденной ревальвации доллара.
Задача № 227
Рассчитайте потери и выгоды США от фактической ревальвации доллара, вызванной девальвацией фунта стерлингов с точки зрения курсовой разницы. Сумма невыполненных контрактов по экспорту США в Англию составляет 20 млн. фунтов стерлингов. Сумма невыплаченных контрактов по импорту из Англии 15 млн. фунтов стерлингов. Девальвация фунта стерлингов: старый курс 2,2 доллара, новый курс 1,8 доллара.
studfiles.net
Контрольная работа по дисциплина «Статистика» — контрольная работа
ханты – мансийский филиалНОУ ВПО «ИНСТИТУТ УПРАВЛЕНИЯ»Кафедра общих гуманитарных, социальных, математических и естественнонаучных дисциплин Контрольная работаДисциплина «Статистика» Вариант №3. Выполнила Е.В. Куликова Шифр студента 13 Группа 41 ФЗС Специальность 080105 «Финансы и кредит» Преподаватель М.Б. Ермолаев г. Ханты-Мансийск 2011 |
Вариант №3.
1. Результаты торговой сессии по акциям АО «ЛУКойл» характеризуются следующими данными:
| Торговая площадка | Средний курс, руб. | Объем продаж, шт. |
| Российская торговая система Московская межбанковская валютная биржа Московская фондовая биржа | 446 449 455 | 138626 175535 200000 |
Рассчитайте средний курс акции по всем трем площадкам вместе взятым.
Решение:
- Известно = 446 , 449, 455
138626, 175535, 200000
Российская торговая система:
Московская межбанковская валютная биржа
Московская фондовая биржа
3) Найдем средний курс акций по всем трем площадкам вместе взятым по формуле средней арифметической взвешенной:
Ответ: средний курс акций составил 450 рублей.
2. Распределение коммерческих банков по величине кредитных вложений характеризуется следующими данными:
| Величина кредитных вложений, млн руб. | До 200 | 200-400 | 400-600 | 600-800 | 800-1000 | 1000 и более | Итого |
| Число банков | 5 | 10 | 8 | 7 | 4 | 2 | 36 |
Определите моду и медиану уровня кредитных вложений, объясните их содержание.
Решение:
1) Найдем модальный интервал с границами 200-400 т.к. он имеет наибольшую частоту - 10.
2) Определим моду по формуле:
3) Найдем накопленные частоты
5+10=15
15+8=23
23+7=30
30+4=34
34+2=36
| Величина кредитных вложений, млн руб. | До 200 | 200-400 | 400-600 | 600-800 | 800-1000 | 1000 и более | Итого |
| Число банков | 5 | 10 | 8 | 7 | 4 | 2 | 36 |
| Накопленные частоты | 5 | 15 | 23 | 30 | 34 | 36 |
4) Найдем медианный интервал 400-600 т.к. общее количество банков 36:2=18
5) Определим медиану по формуле:
Ответ: - уровень кредитных вложений часто встречающихся в интервале 200-400; показывает что до 475 находится 50% вложений и после 475 еще 50%.
3. Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:
| Длина пробега за один рейс, км | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80 и выше | Итого |
| Число рейсов за 1 месяц | 20 | 25 | 14 | 18 | 8 | 5 | 90 |
Определите:
а) среднюю длину пробега за один рейс;
б) среднее квадратическое отклонение;
в) коэффициент вариации.
Оцените количественную однородность совокупности.
Решение:
а) Определим среднюю длину пробега за один рейс по формуле средней арифметической взвешенной:
б) Найдем среднее квадратическое отклонение по формуле:
| Длина пробега за один рейс, км | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80 и выше | Итого |
| Число рейсов за 1 месяц, | 20 | 25 | 14 | 18 | 8 | 5 | 90 |
| Середина интервала, | 35 | 45 | 55 | 65 | 75 | 85 | |
| - 18,2 | - 8,2 | 1,8 | 11,8 | 21,8 | 31,8 | ||
| 331,24 | 67,24 | 3,24 | 139,24 | 475,24 | 1011,24 | ||
| 6624,8 | 1681 | 45,36 | 2506,32 | 3801,92 | 5056,2 | 19715,6 |
Подставим полученные данные в формулу:
в) Найдем коэффициент вариации:
т.к коэффициент вариации V = 27,82% 33%, то количественная совокупность однородная.
Ответ: средняя длина пробега за один рейс = 53,2км; среднее квадратическое отклонение 14,8км; коэффициент вариации 27,82%; количественная совокупность является однородной.
4. Выборочное 5%-ное обследование размеров домохозяйств района, проведенное на основе собственно-случайного бесповторного отбора, позволило получить следующие данные:
| Размер домохозяйства, чел. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Число домохозяйств | 35 | 94 | 167 | 53 | 12 | 4 | 1 |
С вероятностью 0,954 определите по району в целом: а) границы среднего размера домохозяйства; б) границы общей численности населения района.
Решение:
а) Определим границы среднего размера домохозяйств по формуле средней арифметической взвешенной:
б) Найдем среднее квадратическое отклонение по формуле:
| Размер домохозяйства, чел., | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Число домохозяйств, | 35 | 94 | 167 | 53 | 12 | 4 | 1 |
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
| 4 | 1 | 0 | 1 | 2 | 9 | 16 | |
| 140 | 94 | 0 | 53 | 24 | 36 | 16 |
freepapers.ru
УП Рынок ценных бумаг - 2009

41
3. ДЕРИВАТИВЫ
Деривативы – это производные ценные бумаги, выражающие имущественные права (обязательства), возникающие в связи с изменением цены, лежащей в основе данной ценной бумаги биржевого актива. Существуют следующие типы производных финансовых инструментов:
1)форвардные контракты;
2)биржевые опционы;
3)фьючерсные контракты;
4)свопы.
Биржевой опцион – это стандартный биржевой договор на право купить или продать биржевой актив или фьючерсный контракт по цене исполнения до (или на) установленной(ую) даты(у) с уплатой за это право определенной суммы денег, называемой премией. Опционы бывают на покупку (КОЛЛ) или на продажу (ПУТ).
Текущая цена опциона «КОЛЛ» рассчитывается по специальной формуле. Получившая название в честь своих авторов, формула Блэка– Шоулза имеет следующий вид:
V | = N(d )× P− | E | × N(d |
| ) , | |
| 2 | |||||
с | 1 | a | eRt |
| ||
|
|
|
|
| ||
d1 = 1n (Pa /E) +(R + 0,5σ2 )×T , G T
T
d2 = 1n (Pa /E) +(R + 0,5σ2 )×T = d1 − σ
 T , G
T , G T
T
где Vс – текущая цена опциона «КОЛЛ»; Ра – текущая рыночная цена базисного актива; Е – цена исполнения опциона;R – непрерывно начисляемая ставка без риска в расчете на год; Т – время до истечения, представленное в долях в расчете на год;n – натуральный логарифм частного отделения текущей цены актива на цену исполнения опциона; σ – риск базисной обыкновенной акции, измеренный стандартным отклонением доходности акции, представленной как непрерывно начисляемый процент в расчет на год; Е/еRt – дисконтированная стоимость цены исполнения на базе непрерывно начисляемого процента;N(d1) иN(d2) – вероятности того, что при нормальном распределении со средней величиной, равной 0, и стандартным отклонением, равным 1, результат будет соответственно меньшеd1 иd2.

42
В качестве примера рассмотрим опцион «КОЛЛ», который истекает через три месяца (Т=0,25) и имеет цену исполнения 40 долл. (Е=40 долл.), текущая цена 36 долл. (Ра=36 долл.), риск базисной обыкновенной акции 50 % (σ=0,5), а ставка без риска равна 5 % (R=0,05).
С помощью уравнений (48), (49) получим следующие значения d1
и d2:
d1 = 1n (36/40) + (0,05 + 0,5(0,52 ) × 0,25= −0,25 , 0,5
 0,25
0,25
d2 = −0,25 − 0,5
 0,25 = −0,50.
0,25 = −0,50.
По специальной таблице находим величины N(d1) иN(d2):
N(d1) = N(-0,25)=0,4013.
N(d2)= N(-0,50)=0,3085.
Используя уравнение (47), получим действительную стоимость опциона «КОЛЛ»:
Vс | = (0,4013 × 36дол ) − ( |
| 40 дол | ) = 14,45 |
| − 12,19дол. | = 2,26дол . |
e0,05 | ×0,25 × 0,3085 | дол. | |||||
|
|
|
|
|
|
Стоимость опциона непосредственно связана со стоимостью базисного актива.
Внутренняя стоимость = рыночная цена актива - цена исполнения | (50) |
Временнаястоимость = премия по опционувнутренняястоимость | (51) |
Временная стоимость опциона при одном и том же сроке исполнения может существенно отличаться: по мере завершения опциона уменьшается, в начальный момент времени может быть максимальной. Для покупателя опциона, занявшего длинную позицию, каждый день действия опциона сокращает возможность с выгодой для себя его реализовать. Продавцу же ситуация удешевления опциона поможет выгодно его выкупить. Разница между ценой продажи и покупки является прибылью продавца.
Пример. Текущий курс акции равен 10 долл. Цена исполнения 9,8 долл. Премия за опцион «КОЛЛ» была уплачена 0,5 долл. за акцию.
Внутренняя стоимость одной акции по формуле (50) составит: 10 долл. – 9,8 долл. = 0,2 долл.
43
Тогда временная стоимость согласно формуле (51) будет равна 0,5 долл. – 0,2 долл. = 0,3 долл.
Премия опциона КОЛЛ тем выше, чем больше цена спот базисного актива, время до истечения контакта, ставка без риска и чем меньше цена исполнения.
Премия опциона ПУТ тем выше, чем больше цена исполнения, время до истечения контракта и чем меньше цена спот и ставка без риска.
Ряд операций с производными осуществляют с целью хеджирова-
ния.
Для хеджирования своей позиции с помощью опционных контрактов, вкладчик должен определить требуемое число контрактов. Оно рассчитывается по следующей формуле:
Число опционных = Число единиц хеджируемого / Число единиц
|
| в опционном |
контрактов | актива | контракте |
Пример. Инвестор имеет 5 000 акций. Лот биржевого опциона составляет 100 акций.
Тогда число опционных контактов = 5 000 / 100 = 50 шт.
В ряде случаев возникает необходимость хеджировать опционную позицию.
Это можно сделать с помощью показателя дельта.
Дельта – это отношение изменения цены опциона к изменению цены базисного актива.
Дельта показывает, в какой мере изменится цена опциона при изменении цены. Значение дельты говорит о числе единиц актива, которые инвестор должен купить или продать на каждую позицию по опционному контракту. На каждый выписанный опцион КОЛЛ вкладчик должен купить количество базисного актива, равное значению дельта опциона. На каждый купленный опцион КОЛЛ ему следует продать данное количество единиц актива. Покупая опцион ПУТ, инвестор должен купить соответствующее число единиц актива, а продавая опцион ПУТ, – продать данное количество единиц актива.
Пример. Инвестор продал 500 опционов на 500 акций. Дельта опциона равна 0,4. Для хеджирования опционной позиции ему следует купить:
0,4 × 500 акций = 200 акций.
44
Пусть цена акций упала на 1 руб., тогда по акциям вкладчик теряет 200 руб. При этом также падает цена опциона на 0,4 руб. и соответственно стоимость опционной позиции уменьшается на:
0,4 × 5000 опционов = 200 руб.
Проигрыш по акциям компенсируется выигрышем по опционам, так как при закрытии опционной позиции контракты будут выкупаться на 200 руб. дешевле по сравнению с ценой продажи.
Осуществление хеджевых операций при определенном направлении движения цены со стороны инвестора представлено в табл. 3.1.
|
|
| Таблица 3.1 |
Действия инвестора при хеджировании |
| ||
|
|
|
|
Хеджирование позиции | Опцион КОЛЛ |
| Опцион ПУТ |
Понижение цены актива | продать |
| купить |
Повышение цены актива | купить |
| продать |
Фьючерсный контракт – это стандартный биржевой договор ку-пли-продажибиржевого актива в определенный момент времени в будущем по цене, установленной сделкой в момент ее заключения.
Математический расчет стоимости фьючерсного контракта зависит от того, какие факторы учитываются. Например, учет постоянных факторов может быть осуществлен по формуле
| Са = Ца + Ца × П × | Д | , | (52) |
|
|
| ||
| 360 |
|
| |
где | Са – стоимость фьючерсного контракта на биржевой | актив А; | ||
Ца – | рыночная цена актива А на физическом рынке, ден. ед.; П – бан- | |||
ковский процент по депозитам, %; Д – число дней до окончания срока действия фьючерсного контракта или его закрытия.
Если биржевой актив сам по себе приносит определенный доход, например, дивиденд по акции или процент по облигации, то этот доход следует вычесть из банковской процентной ставки и предыдущая формула примет следующий вид:
Са | = Ца | + Ца | × (П - Па ) × | Д |
| (53) |
360 , |
| |||||
|
|
|
|
| ||
где Па – средний размер дивиденда по акции или процента по облигации.
Например, Ца=100 руб., П=20 % годовых, Па=10 % (в год), Д=60 дн.
45
Подставляя эти значения в формулу, рассчитаем стоимость фьючерсного контракта на покупку одной акции по текущей рыночной цене 100 руб. и с ежегодным размером дивиденда в 10 % с поставкой через 60 дней при среднем рыночном проценте 20 % годовых.
С |
| = 100 руб. + 100 руб× (0,2 - 0,1) × | 60 | = 100 руб. + 1,67 руб. = 101,67 руб. |
а |
| |||
| 360 |
| ||
|
|
| ||
Если в качестве актива выступает облигация, то цена, по которой может быть поставлена облигация, рассчитывается по следующей формуле:
Цена | Котировочная | Коэффициент | (54) | |||
| × |
|
| × Накопленные |
| |
поставки = цена | конверсии |
| ||||
облигации |
|
|
| проценты |
| |
|
|
|
|
| ||
Цена | Котировочная | Коэффициент |
|
| (55) | |
| × конверсии | = | наиболее выгодная цена | , | ||
спот - цена | ||||||
|
|
|
|
| покупки |
|
где Цена спот – цена актива на кассовом рынке (расчет в течение установленного времени).
Разница между ценой покупки и ценой поставки будет доходом продавца контракта.
При определении фьючерсной цены облигации с купонными выплатами используется следующее уравнение:
F = (S− J)× (l+ r)t , | (56) |
где S – полная цена облигации в момент заключения контракта, ден. ед.;J – приведенная стоимость купона;t – период обращения облигации, лет.
Пример. Определите фьючерсную цену облигации на момент истечения контракта, имея следующие данные. Срок действия контракта – 210 дней. Непрерывно начисляемая ставка без риска – 10 %. Предлагается, что по облигации купон составит 11,5 % при выплате 2 раза в год. Чистая цена «спот» облигации равна 110 000 тыс. долл., коэффициент конверсии – 1,35. Выплата по купону, предшествующая заключению контракта, состоялась 30 дней назад, а следующий будет выплачен через 152 дня.

46
Определим полную цену «спот» облигации на момент заключения контракта. Она равна:
110000 + | 6325 × 30 | = 111042,5 | долл., |
| |||
182 |
|
| |
где 6 325 – купонная доходность за 182 дня.
Рассчитаем приведенную стоимость купона, который будет вы-
плачен через 152 дня (152:365=0,4164)
6325 | = 5515,59 долл. |
(1+ 0,1)0,4164 |
Затем находим полную цену облигации на момент истечения кон-
тракта (210:365=0,5753):
(111042,5 − 5515,59)(1 + 0,1)0,5753 = 111675,7долл.
В биржевых расчетах используются следующие зависимости:
Доходность актива = 100% - фьючерсная цена (%). | (57) |
Пример. Если доходность облигации – 10 %, тогда фьючерсная цена = 100%-10%=90 %.
Минимальное изменение цены на один базисный пункт называется шаг и определяется как:
Цена шага = | n | × N × один базисный пункт, | (58) |
365 |
| ||
|
|
|
где n – срок действия контракта, дней;N – номинал базисного актива, руб.
Число шагов = | F2-F1 | , | (59) |
|
|
шаг цены
где F1 – фьючерсная цена в моментt1;F2 – фьючерсная цена в моментt2.
| число | изменение | (60) |
|
| ||
Выигрыш / Потери | = контрактов× числа шагов | × цена одного шага | |
от сделки |
|
|
|

47
Пример. Определите потери для сделки инвестора по фьючерсному контракту сроком 91 день при номинале 100 000 руб., если он приобрел контракт за 90 000 руб., а через несколько дней продал за 89 950 руб. Шаг цены равен одному базисному пункту.
Цена шага = 100000 × 91 × 0,0001 = 2,49 руб. 365
Цена актива по фьючерсу изменилась на 89950 − 90000 = −5 шагов
10
Потери от сделки = 1× 5× 2,49 = 12,45 рублей.
Задача 1. Текущий курс акций корпорации «АвтоВАЗбанк» – 10 000 руб. Первый игрок рассчитывает на снижение, а второй – на повышение курсовой стоимости этих акций. Второй игрок берет на себя обязательство купить акции у первого игрока по курсу 9 200 руб. Премия по контракту установлена 80 руб. за акцию. В процессе торгов курс акций снизился до уровня 8 700 руб. за акцию. Как следует поступить первому игроку?
Задача 2. Текущая курсовая стоимость акции корпорации «Кузбассоцбанк» – 1 200 руб. за акцию при номинале в 1 000 руб. Один инвестор полагает, что курсовая стоимость и дальше будет расти. Он покупает у другого инвестора, который противоположного мнения относительно роста цены данной акции. Опцион на покупку одного лота этих акций по цене 1 250 руб. за акцию. Цена опциона (премия) составляет 15 000 руб. Срок исполнения опциона – через три месяца. В день исполнения контракта курс акций составил 1 380 руб. Как следует поступить первому инвестору и какой финансовый результат его ожидает в случае предъявления опциона к исполнению?
Задача 3. Текущая курсовая стоимость акции корпорации «Западуралбанк» 1 750 руб. при номинале 1 500 руб. Первый инвестор продает опцион на продажу, в котором обязуется продать второму игроку полный лот этих акций по курсу 1 740 руб. за штуку по цене опциона 10 000 руб. Срок исполнения контракта – один месяц. В день исполнения опциона курс акций снизился и составил 1 570 руб. за акцию. Какие действия должен предпринять второй игрок и какой финансовый результат его ожидает в случае предъявления опциона к исполнению?
48
Задача 4. Первый ваучерный инвестиционный фонд приобрел на фондовой бирже 5 000 акций преуспевающей компании «Торговый дом “ Латония”» по курсу 1 350 руб. за акцию при их номинальной стоимости 1 000 руб. В связи с внезапным ухудшением финансовых показателей фирмы ожидается снижение курса этих акций, что грозит существенными потерями для инвесторов инвестиционного фонда.
Менеджер портфеля ценных бумаг инвестиционного фонда страхует вероятные убытки путем выписки 50 опционов на покупку (КОЛЛ) по курсу 1 400 руб. и продает их по цене 10 000 руб. за опцион сроком на один месяц. За это время курс акций ТД «Латония» действительно упал до 1 290 руб. за акцию, но в конце месяца вследствие изменения рыночной конъюнктуры резко возрос до 1 460 руб. Требуется определить финансовый результат от операций с опционами для инвестиционного фонда.
Задача 5. Определите общие затраты на покупку опциона пакета акции«МДМ-Банк»,имея следующие данные:
Сумма (величина пакета из 1 000 акций) | 100 тыс. руб. |
Срок | 3 месяца |
Цена исполнения опциона (страйк цена) | 3 200 руб. за акцию |
Премия | 100 руб. за 1 акцию |
Стиль | европейский |
Задача 6. На срочном рынке открыта короткая позиция по фьючерсу на поставку 200 акций через 4 месяца по цене 40 руб. за акцию. Определите результаты от операции продавца, если в момент исполнения контракта рыночная цена акции составила:
а) 45 руб.; б) 40 руб.;
в) 38 руб.
Задача 7. Рассчитайте стоимость фьючерсного контракта на акции КБ«МДМ-Банк»,которые на вторичном рынке реализуются по 1 890 руб. при номинале 1 000 руб. До исполнения фьючерса осталось 80 дней. Альтернативное вложение в банк возможно под 25 % годовых.
Сделайте расчет, если: а) начисляется дивиденд 30 % годовых; б) дивиденд не начисляется.
Задача 8. Определите фьючерсную цену облигации с купоном 12 %, выплата по которому происходит 2 раза в год. Чистая цена «спот» облигации составляет 120 000 руб., коэффициент конверсии – 1,4. Выплата по купону, предшествующему заключению контракта, состоялась
49
20 дней назад, а следующий будет выплачен через 162 дня. Срок действия контракта – 240 дней, непрерывно начисляемая ставка без риска –
10 %.
Задача 9. На срочном рынке был реализован один фьючерсный контракт на средневзвешенный курс КГО с исполнением через 2 месяца по цене 81,6 %. Средневзвешенный курс ГКО в этот день составил 68,21 %. На следующей сессии этим же покупателем совершена покупка такого же контракта по цене 80 % при средневзвешенном курсе ГКО 68,63 %. Каков финансовый результат от данных операций, если шаг изменения цены контракта 0,01 % номинала ГКО, а цена шага 100 руб.?
Задача 10. На рынке дивидендов приобретен опцион пут на облигацию с ценой исполнения 80 тыс. руб. Цена опциона (премия), уплаченная при этом продавцу, составила 7 тыс. руб. На момент исполнения опциона курс облигации составил 70 тыс. руб. Определите финансовые результаты операции.
Задача 11. Определите финансовые результаты исполнения опциона «КОЛЛ» на акцию «AVVA» с ценой исполнения 150 тыс. руб., если цена опциона (премия), уплаченная продавцу, составила 15 тыс. руб. На момент погашения опциона курс акции «AVVA» составил 200 тыс. руб.
Задача 12. Инвестором был приобретен фьючерсный контракт на облигации сроком действия 240 дней с купонной ставкой 13 % и выплатой 2 раза в год. Непрерывно начисляемая ставка без риска – 10 %. Чистая цена «спот» облигации составляет 1 200 руб., а коэффициент конверсии – 1,35. Выплата по купону, предшествующему заключению контракта, состоялась 45 дней назад, а следующий будет выплачен через 137 дней. Необходимо определить фьючерсную цену.
Задача 13. Рассчитайте финансовые результаты сделки со фьючерсным контракта сроком на 180 дней и номиналом 10 000 руб. Инвестором данный контракт приобретен за 9 850 руб. и продан через некоторое время по цене 9 625 руб. Считать, что шаг цены равен одному базисному пункту.
Задача 14. Фьючерсный контракт на актив номиналом 10 000 руб. выписан сроком на 60 дней. Инвестор приобретает контракт по 110 000 руб. и перепродает за 115 000 руб. Определите результаты сделки инвестора при условии, что шаг цены равен одному базисному пункту.
50
Задача 15. Рассчитайте общие затраты на покупку опциона пакета акцийХ, имея следующие данные:
Сумма (величина пакета из 100 акций | 150 тыс. руб. |
номиналом 1 000 руб.) |
|
Срок | 6 месяцев |
Цена исполнения опциона (страйк цена) | 2 800 руб. за 1 акцию |
Премия | 75 руб. за 1 акцию |
Стиль | американский |
Задача 16. На фондовой бирже заключен фьючерсный контракт на фондовый индекс на 3 месяца. Рыночная процентная ставка равна 10 %. Дивиденды по акциям, составляющим индекс, не выплачиваются. Значение индекса на начало периода равно 10 000 единиц. Рассчитайте цену данного фьючерса.
Задача 17. Определите полугодовой фьючерсный курс валюты, если курс доллара составляет 27 руб., процентная ставка по долларовым депозитам на 6 месяцев – 3,5 % годовых.
Задача 18. Брокер продал КОЛЛ опцион на пакет акций со страйком 20 руб. по цене 0,7 руб. Через 3 месяца к моменту исполнения опциона рыночная цена выросла до 23 руб. Сопоставьте доходы (убытки) брокера для следующих случаев:
а) пакет акций есть в наличии и был куплен по цене 17 руб.; б) пакет акций есть в наличии и был куплен по цене 20,35 руб.; в) пакет акций есть в наличии и был куплен по цене 21,5 руб.; г) акций в наличии нет.
Задача 19. Премия опциона КОЛЛ равна 20 руб., цена спот – 130 руб., цена исполнения – 125 руб. Определите внутреннюю и временную стоимость опциона.
Задача 20 . Брокер продалКОЛЛ-опционна пакет акций со страйком 20 руб. по цене 0,7 руб. Через 3 месяца к моменту исполнения опциона рыночная цена выросла до 23 руб. Сопоставьте доходы (убытки) брокера для следующих случаев:
а) пакет акций есть в наличии и был куплен по цене 17 руб.; б) пакет акций есть в наличии и был куплен по цене 20,35 руб.; в) пакет акций есть в наличии и был куплен по цене 21,5 руб.; г) акций в наличии нет.
studfiles.net