Курс доллара США (usd) в банках, выгодный обмен доллара США на рубли, лучший курс

На 5 марта 2023, 16:36

У меня есть

1 USD = 75.46 RUB

Доллар США

Хочу купить

1 RUB = 0.013 USD

Российский рубль

Курс доллара в банках

USDEURCNYAMDAUDAZNBGNCADCHFCZKGBPINRJPYKGSKRWKZTNOKPLNSEKSGDTRY

Все валюты

Все банки

График изменения курса доллара

по курсу ЦБ

НеделяМесяцГод

Нет данных, попробуйте изменить параметры поиска

Курсы других валют в Москве

На 5 марта 2023, 00:14

Курс доллара на сегодня и завтра

Зачастую, чтобы вести успешный бизнес и быть уверенным в завтрашнем дне необходимо знать всё о стоимости валюты на сегодня и завтра. Причем, чем раньше вам будет известен завтрашний курс доллара, тем больше конкурентных преимуществ вы получите.  Курс доллара на сегодня и завтра может существенно отличаться, сейчас всего за 24 часа доллар может вырасти по отношению к рублю или, наоборот, стать несколько дешевле. На этой странице в режиме онлайн вы сможете просмотреть самые выгодные курсы доллара на сегодня и завтра почти во всех банках. Воспользовавшись калькулятором обмена, выставив нужный режим «покупка» или «продажа», вы сможете сделать точные расчеты.

Курс доллара к рублю в России

Сегодняшний курс доллара к рублю в России весьма нестабилен.  Чтобы обменять свои рубли на доллары или, наоборот, нужно постараться найти самый выгодный курс американской валюты относительно отечественного рубля. Если речь идет об обменниках, то отметим, что самая высокая котировка  не всегда бывает самой выгодной. Зачастую, в таком случае с вас попросят комиссионные. Иногда к обмену принимаются только определенные купюры номиналом не менее 50 долларов. Курс валюты формируется Центробанком РФ и зависит от итогов торгов, проходящих на Московской бирже. Курс доллара в разных банках может отличаться, но он остается в пределах допустимого коридора.

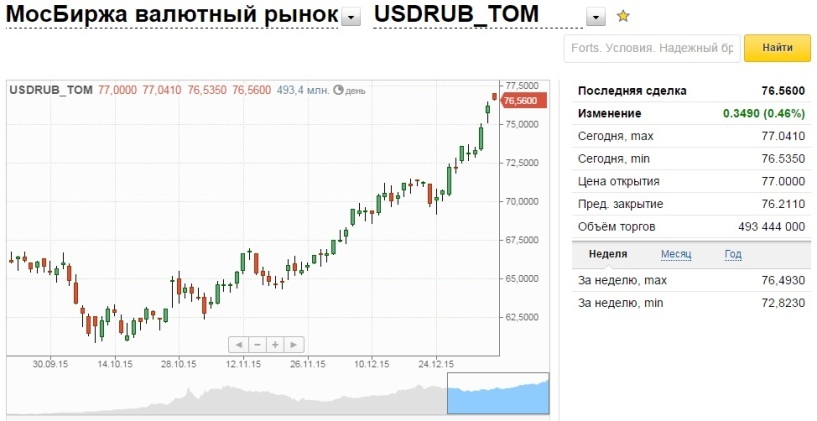
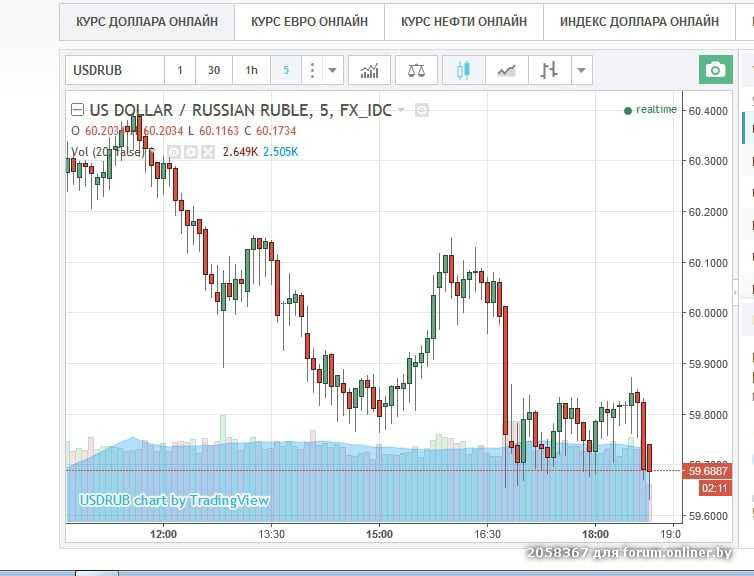
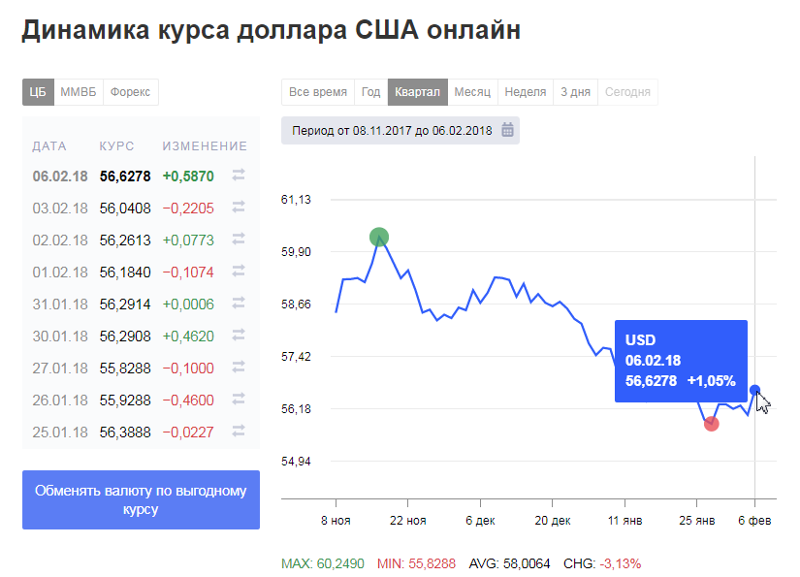
Курс доллара онлайн в реальном времени

Посмотреть курс доллара онлайн в реальном времени можно на сайте Центробанка. Официальный курс валюты рассчитывается после индексной сессии на ММВБ, которая проходи в будни в утренние часы – с 10.00 до 11.30 по МСК. Также в реальном времени можно видеть обновление графиков курсов валют. На графиках отображены завтрашние цены доллара и Евро. Графики дают представление о курсе валют еще до объявления официальных курсов Центробанка. Если нефть дешевеет, то обычно рубль падает вместе  с ней, если нефть становится дороже, с рублем происходит то же самое. Для экономики России цена нефти – наиважнейший показатель.

Курс доллара в обменниках

Курс доллара в разных обменниках может существенно отличаться, но, все же, он не будет выходить за пределы валютного коридора. Прежде чем ехать в банк для обмена долларов на рубли или, наоборот, проверьте на нашем сайте курс в обменниках. Также учитывайте, что менять большую сумму куда выгоднее, чем пару сотен долларов. Обычно точки обмена на большие суммы валюты делают котировки значительно выгоднее.  Но бывают и скрытые комиссии, например, при обмене маленькой суммы, вы платите определенный процент. 

Курс обмена доллара

Перед совершением валютной операции в банке, всегда уточняйте курс обмена доллара. Курс обновляется 2-3 раза в сутки. Чтобы выбрать самый выгодный курс, просмотрите предложения по обмену валюты всех банков, обзор которых мы предоставляем. Если вам необходимо проверить курс обмена валюты в конкретном банке, и вы не хотите искать его в таблице, просто воспользуйтесь поиском в верхнем правом углу. Введите название банка и нажмите поиск. Также вы можете просмотреть выгодный курс продажи доллара.

История доллара 

Само слово «доллар» произошло от немецкого «таллер» — это средневековая монета, бывшая в обиходе в Германии в 1519-м году. Невероятно, но доллар является ровесником Америки. В 17-м веке этим словом называли все мелкие монеты и разменные деньги. Знаменитый значок «$» появился, благодаря смекалке американских колонистов. В наши дни бумагу для производства долларов (купюр) делают из хлопка и льна в соотношении 75% к 25%. Выходит бархатистая, слегка шершавая на ощупь бумага.  Сейчас доллар США носит лавры основной резервной мировой валюты. 

Евро онлайн торги в реальном времени

Курс евро на торгах и сами торги ММВБ регулируются Центральным банком РФ, осуществляющим функции на основе закона о госзакупках и закона о валютном регулировании и контроле. Евро одна из самых популярных валют на мировой бирже. Она обладает достаточно высоким уровнем волатильности, а потому самые волатильные пары на бирже торгуются именно с участием евро.

Евро — валюта стран Евросоюза, одна из самых молодых денежных единиц мира. Полноценно функционировать она стала только с 1999 года, однако даже за это короткое время европейская денежная единица стала одной из самых сильных в мире и поддерживает экономику таких стран, как Франция, Германия, Испания и др. Европейская валюта привлекает инвесторов, предпочитающих конвертировать свои капиталы в стабильный евро, а на бирже Форекс самые волатильные пары торгуются исключительно с участием этой валюты Старого Света. Одним из самых популярных видов торгов являются торги онлайн.

Курс евро на торгах в реальном времени

Евро подвергается влиянию факторов, влияющих и на доллар. Во-первых, стабильность европейской валюты определяет экономика входящих в Евросоюз стран, а значит прирост валового национального продукта, показатели процентной ставки, промышленное производство, а также уровень безработицы и инфляция стран содружества в совокупности вносят значительный вклад в формирование стоимости этой денежной единицы. Поэтому также важны и решения Европейского Центрального банка по проблемным странам содружества. Вывод стран – членов Евросоюза из кризиса требует взвешенного общего решения, без которого европейская валюта может значительно упасть. Кроме того, на курс евро влияет доллар – спрос на денежную единицу Старого Света повышается, когда падает курс валюты США. Также на стоимость евро влияют другие факторы, такие как заявления об индексе деловых ожиданий от политиков или руководителей финансовых институтов, прогнозы аналитических агентств, политическая нестабильность в Евросоюзе и в мире. Экономисты рассчитывают стоимость евро по отношению к валютам другим стран, исходя из объема выпущенной валюты и уровня эффективности экономики Евросоюза.

Курс евро на торгах и сами торги ММВБ регулируются Центральным банком РФ, осуществляющим функции на основе закона о госзакупках и закона о валютном регулировании и контроле. Евро одна из самых популярных валют на мировой бирже. Она обладает достаточно высоким уровнем волатильности, а потому самые волатильные пары на бирже торгуются именно с участием евро. Торги онлайн в реальном времени привлекают все больше игроков, а стабильность «представительницы» Евросоюза позволяет получить высокую прибыль. Кроме того, высокая ликвидность этой валюты обеспечивает определенную безопасность.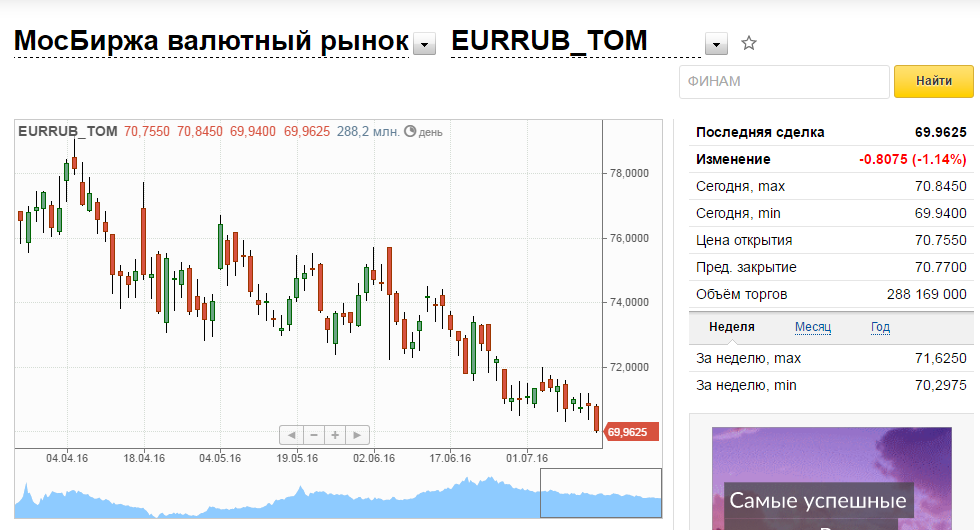 Однако даже при всем этом стоит помнить, что евро, как и любая денежная единица, может повести себя непредсказуемо, а значит следует внимательно следить за ситуацией на валютном рынке.

Евро на онлайн торгах ММВБ

Качественный и грамотный анализ валютного рынка – главное, чем должен владеть трейдер, желающий вести торг ММВБ. Евро и денежные единицы других стран требуют от него точного выявления закономерностей ценовых реакций и аккуратной оценки ситуации на валютном рынке в отношении валюты Старого Света. Процесс торговли может значительно упростить внимание к тому, что волатильность евро увеличивается в периоды европейской торговой сессии. Это поможет принять наиболее выгодное решение, также, как и привычка отслеживать торги онлайн.

Моделирование молекулярной фотодинамики в больших временных масштабах

1. Креспо-Отеро Р., Барбатти М. 2018.
Последние достижения и перспективы неадиабатической смешанной квантово-классической динамики. хим. преп.
118 , 7026-7068. ( 10.1021/acs.chemrev.7b00577) [PubMed] [CrossRef] [Google Scholar]

2. Curchod BF, Martinez TJ. 2018.
Ab initio неадиабатическая квантовая молекулярная динамика. хим. преп.
118 , 3305-3336. ( 10.1021/acs.chemrev.7b00423) [PubMed] [CrossRef] [Google Scholar]

3. Нельсон Т.Р.
и др.
2020.
Неадиабатическая молекулярная динамика возбужденного состояния: теория и приложения для моделирования фотофизики протяженных молекулярных материалов. хим. преп.
120 , 2215-2287. ( 10.1021/acs.chemrev.9b00447) [PubMed] [CrossRef] [Google Scholar]

4. Vacher M, Mendive-Tapia D, Bearpark MJ, Robb MA. 2014.
Метод Эренфеста второго порядка. Теор. хим. Акк.
133 , 1505. ( 10.1007/s00214-014-1505-6) [CrossRef] [Google Scholar]

5. Лингерфельт Д.Б., Уильямс-Янг Д.Б., Петроне А., Ли С. 2016.
Прямая ab initio (мета-) динамика прыжков по поверхности. Дж. Хим. Теория вычисл.
12 , 935-945. ( 10.1021/acs. jctc.5b00697) [PubMed] [CrossRef] [Google Scholar]

6. Ниджамудхин А., Акимов А.В. 2017.
Динамика возбужденных состояний в двумерных гетероструктурах: SiR/TiO ₂ и GeR/TiO ₂ (R = H, Me) как перспективные фотокатализаторы. Дж. Физ. хим. С
121 , 6520-6532. ( 10.1021/acs.jpcc.7b00545) [CrossRef] [Google Scholar]

7. Акимов А.В. 2017.
Стохастические и квазистохастические гамильтонианы для долговременной неадиабатической молекулярной динамики. Дж. Физ. хим. лат.
8 , 5190-5195. ( 10.1021/acs.jpclett.7b02185) [PubMed] [CrossRef] [Google Scholar]

8. Барбатти М. 2020.
Моделирование возбуждения солнечным светом в смешанной квантово-классической динамике. Дж. Хим. Теория вычисл.
16 , 4849-4856. ( 10.1021/acs.jctc.0c00501) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

9. Вестермайр Дж., Гастеггер М., Менгер MFSJ, Май С., Гонсалес Л., Маркетанд П. 2019.
Машинное обучение позволяет моделировать молекулярную фотодинамику в долгосрочном масштабе. хим. науч.
10 , 8100-8107. ( 10.1039/C9SC01742A) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

10. Jingbai L, Patrick R, André E, Pascal F, Steven L. 2020.
Наносекундное фотодинамическое моделирование цис-транс-изомеризации стало возможным благодаря машинному обучению. ChemRxiv. ( 10.26434/chemrxiv.13047863) [Перекрестная ссылка]

11. Лан Дж., Капил В., Гаспаротто П., Чериоти М., Яннуцци М., Рыбкин В.В. 2021.
Моделирование призрака: квантовая динамика сольватированного электрона. Нац. коммун.
12 , 766. ( 10.1038/s41467-021-20914-0) [ЧВК бесплатная статья] [PubMed] [CrossRef] [Google Scholar]

12. Акимов А.В. 2021.
Расширение временных масштабов неадиабатической молекулярной динамики с помощью машинного обучения во временной области. Дж. Физ. хим. лат.
12 , 12 119-12 128.( 10.1021/acs.jpclett.1c03823) [PubMed] [CrossRef] [Google Scholar]

13. Li J, Reiser P, Boswell BR, Eberhard A, Burns NZ, Friederich P, Lopez SA. 2021.
Автоматическое обнаружение механизмов фотоизомеризации с помощью моделирования фотодинамики наносекундного машинного обучения. хим. науч.
12 , 5302-5314. ( 10.1039/D0SC05610C) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

14. Dral PO, Barbatti M. 2021.
Молекулярные возбужденные состояния через призму машинного обучения. Нац. Преподобный Хим.
5 , 388-405. ( 10.1038/s41570-021-00278-1) [CrossRef] [Google Scholar]

15. Вестермайр Дж., Маркетан П. 2020.
Машинное обучение для электронно-возбужденных состояний молекул. хим. преп.
5 , 388-405. ( 10.1021/acs.chemrev.1020c00749) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

16. Stevens ARH, Bellstedt S, Elahi PJ, Murphy MT. 2020.
Необходимость сокращения выбросов углерода в астрономии. Нац. Астрон.
4 , 843-851. ( 10.1038/s41550-020-1169-1) [CrossRef] [Google Scholar]

17. Korth M, Thiel W. 2011.
Сравнение полуэмпирических методов термохимии, кинетики и нековалентных взаимодействий: методы OMx почти так же точны и надежны, как методы DFT-GGA для органических молекул. Дж. Хим. Теория вычисл.
7 , 2929-2936. (10.1021/ct200434a) [PubMed] [CrossRef] [Google Scholar]

18. Accomasso D, Granucci G, Wibowo M, Persico M. 2020.
Эффекты делокализации в синглетном делении: сравнение моделей с двумя и тремя взаимодействующими молекулами. Дж. Хим. физ.
152 , 244125. (10.1063/5.0009914) [PubMed] [CrossRef] [Google Scholar]

19. Грануччи Г., Тониоло А. 2000.
Молекулярные градиенты для полуэмпирических волновых функций КИ с плавающими молекулярными орбиталями заполнения. хим. физ. лат.
325 , 79-85. ( 10.1016/S0009-2614(00)00691-6) [CrossRef] [Google Scholar]

20. Kranz JJ, Elstner M, Aradi B, Frauenheim T, Lutsker V, Garcia AD, Niehaus TA. 2017.
Зависимое от времени расширение метода сильной связи на основе дальнодействующего скорректированного функционала плотности. Дж. Хим. Теория вычисл.
13 , 1737-1747. ( 10.1021/acs.jctc.6b01243) [PubMed] [CrossRef] [Google Scholar]

21. Домингес А., Аради Б., Фрауэнхайм Т., Луцкер В., Нихаус Т.А. 2013.
Расширения подхода сильной связи, основанного на зависящем от времени функционале плотности. Дж. Хим. Теория вычисл.
9 , 4901-4914. ( 10.1021/ct400123t) [PubMed] [CrossRef] [Google Scholar]

22. Акимов А.В., Преждо О.В. 2013.
Программа PYXAID для неадиабатической молекулярной динамики в системах конденсированного состояния. Дж. Хим. Теория вычисл.
9 , 4959-4972. ( 10.1021/ct400641n) [PubMed] [CrossRef] [Google Scholar]

23. Ван Л, Лонг Р, Преждо О.В. 2015.
Моделирование ab initio во временной области фотоиндуцированной динамики на наноразмерных интерфейсах. Анну. Преподобный физ. хим.
66 , 549-579. ( 10.1146/annurev-physchem-040214-121359) [PubMed] [CrossRef] [Google Scholar]

24. Smith BR, Bearpark MJ, Robb MA, Bernardi F, Olivucci M. 1995.
Классическая динамика волновых пакетов через коническое пересечение — приложение к фотохимии S ₁ /S ₀ бензола. хим. физ. лат.
242 , 27-32. ( 10.1016/0009-2614(95)00718-J) [CrossRef] [Google Scholar]

25. Пал С., Триведи Д.Дж., Акимов А.В., Аради Б., Фрауенхайм Т., Преждо О.В. 2016.
Неадиабатическая молекулярная динамика для систем с тысячей атомов: жесткий подход к PYXAID. Дж. Хим. Теория вычисл.
12 , 1436-1448. ( 10.1021/acs.jctc.5b01231) [PubMed] [CrossRef] [Google Scholar]

26. Maitra NT. 2006.
О коррелированной электронно-ядерной динамике с использованием теории функционала плотности, зависящей от времени. Дж. Хим. физ.
125 , 014110. (10.1063/1.2210471) [PubMed] [CrossRef] [Google Scholar]

27. Dral PO, von Lilienfeld OA, Thiel W. 2015.
Машинное обучение параметров для точных полуэмпирических квантово-химических расчетов. Дж. Хим. Теория вычисл.
11 , 21:20-21:25. ( 10.1021/acs.jctc.5b00141) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

28. Elstner M, Seifert G. 2014.
Плотная функциональная плотная связка. Фил. Транс. Р. Соц. А
372 , 20120483. (10.1098/rsta.2012.0483) [PubMed] [CrossRef] [Google Scholar]

29. Leggett AJ, Chakravarty S, Dorsey AT, Fisher MPA, Garg A, Zwerger W. 1987.
Динамика диссипативной системы с двумя состояниями. Преподобный Мод. физ.
59 , 1-85. ( 10.1103/RevModPhys.59.1) [CrossRef] [Google Scholar]

30. Weiss U. 1999.
Квантовые диссипативные системы. Сингапур: Мировой научный. [Google Scholar]

31. Mendive-Tapia D, Mangaud E, Firmino T, de la Lande A, Desouter-Lecomte M, Meyer H-D, Gatti F. 2018.
Многомерное квантово-механическое моделирование переноса электронов и электронной когерентности в растительных криптохромах: роль начальных условий ванны. Дж. Физ. хим. Б
122 , 126-136. ( 10.1021/acs.jpcb.7b10412) [PubMed] [CrossRef] [Google Scholar]

32. Тамура Х., Мартинаццо Р., Рукенбауэр М., Бургхардт И. 2012.
Квантовая динамика сверхбыстрого переноса заряда на гетеропереходе олиготиофен-фуллерен.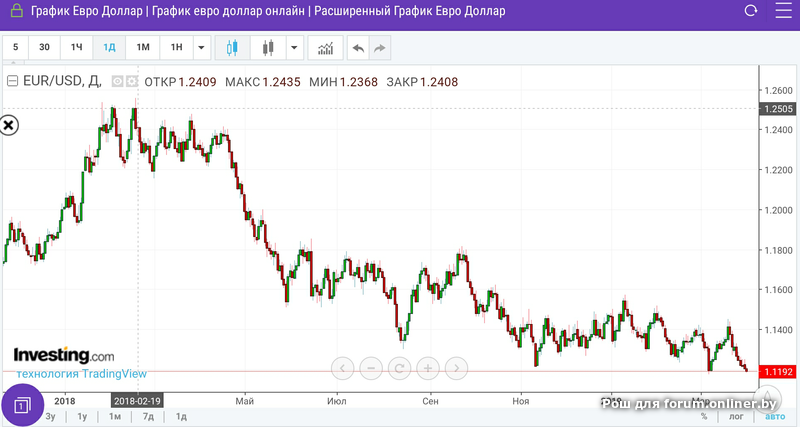 Дж. Хим. физ.
137 , 540. ( 10.1063/1.4751486) [PubMed] [CrossRef] [Google Scholar]

33. Макри Н. 1999.
Приближение линейного отклика и его поправки низшего порядка: функциональный подход влияния. Дж. Физ. хим. Б
103 , 2823-2829. ( 10.1021/jp9847540) [CrossRef] [Google Scholar]

34. Келли А., Маркланд Т.Э. 2013.
Эффективный и точный поверхностный скачок для долговременной неадиабатической квантовой динамики. Дж. Хим. физ.
139 , 014104. ( 10.1063/1.4812355) [PubMed] [CrossRef] [Google Scholar]

35. Ван Х., Сонг Х., Чендлер Д., Миллер У.Х. 1999.
Квазиклассическое исследование электронно-неадиабатической динамики в конденсированной фазе: проблема спиновых бозонов со спектральной плотностью Дебая. Дж. Хим. физ.
110 , 4828-4840. ( 10.1063/1.478388) [CrossRef] [Google Scholar]

36. Chen H-T, Reichman DR. 2016.
О точности динамики поверхностных прыжков в неадиабатических задачах с конденсированной фазой. Дж. Хим. физ.
144 , 094104. (10.1063/1.4942867) [PubMed] [CrossRef] [Google Scholar]

37. Wang H, Thoss M. 2008.
От когерентного движения к локализации: динамика спин-бозонной модели при нулевой температуре. New J. Phys.
10 , 115005. ( 10.1088/1367-2630/10/11/115005) [CrossRef] [Google Scholar]

38. Tempelaar R, Reichman DR. 2017.
Обобщение поверхностных скачков с наименьшим числом переключений для когерентности. Дж. Хим. физ.
148 , 102309. (10.1063/1.5000843) [PubMed] [CrossRef] [Google Scholar]

39. Landry BR, Falk MJ, Subotnik JE. 2013.
Связь: правильная интерпретация поверхностных траекторий прыжков: как рассчитать электронные свойства. Дж. Хим. физ.
139 , 211101. ( 10.1063/1.4837795) [PubMed] [CrossRef] [Google Scholar]

40. Джейн А., Суботник Дж.Е. 2015.
Прыжки по поверхности, теория переходного состояния и декогеренция. II. Константы теплового режима и подробный баланс. Дж.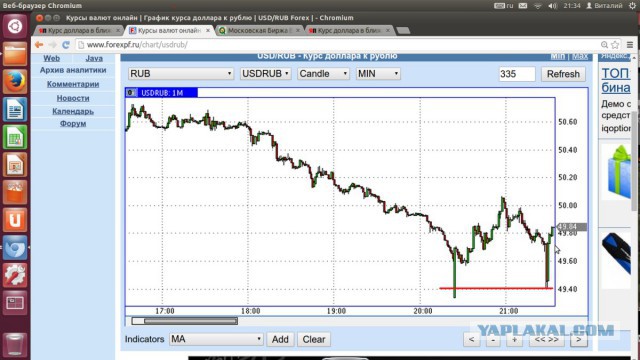 Хим. физ.
143 , 134107. (10.1063/1.4930549) [PubMed] [CrossRef] [Google Scholar]

41. Hughes KH, Christ CD, Burghardt I. 2009.
Представление немарковской динамики в эффективном режиме: иерархическая аппроксимация спектральной плотности. II. Применение к неадиабатической динамике, вызванной окружающей средой. Дж. Хим. физ.
131 , 124108. (10.1063/1.3226343) [PubMed] [CrossRef] [Google Scholar]

42. Мак Кернан Д., Чиккотти Г., Капрал Р. 2002.
Прыжковая динамика системы спиновых бозонов. Дж. Хим. физ.
116 , 2346-2353. ( 10.1063/1.1433502) [CrossRef] [Google Scholar]

43. Бен-Нун М., Мартинес Т.Дж. 2007.
Непрерывный метод нереста для неадиабатической динамики и проверка для проблемы спинового бозона при нулевой температуре. Изр. Дж. Хим.
47 , 75-88. ( 10.1560/IJC.47.1.75) [CrossRef] [Google Scholar]

44. Коппель Х., Домке В., Седербаум Л.С. 1984.
Многомодовая молекулярная динамика за пределами приближения Борна–Оппенгеймера. Доп. хим. физ.
57 , 59-246. ( 10.1002/9780470142813.ch3) [CrossRef] [Google Scholar]

45. Williams DMG, Eisfeld W. 2018.
Диабатизация нейронной сети: новый анзац для точных многомерных связанных поверхностей потенциальной энергии. Дж. Хим. физ.
149 , 204106. (10.1063/1.5053664) [PubMed] [CrossRef] [Google Scholar]

46. Shen Y, Yarkony DR. 2020.
Построение квазидиабатических гамильтонианов, которые точно представляют определенные из первых принципов адиабатические электронные состояния, связанные коническими пересечениями, для систем порядка 15 атомов. Приложение к фотоэлектронному отрыву циклопентоксида в полном объеме 39степени свободы. Дж. Физ. хим. А
124 , 4539-4548. ( 10.1021/acs.jpca.0c02763) [PubMed] [CrossRef] [Google Scholar]

47. Левек С., Комайнда А., Тайеб Р., Кеппель Х. 2013.
Ab initio квантовое исследование фотодинамики и спектра поглощения связанных состояний 11A2 и 11B1 SO ₂ . Дж.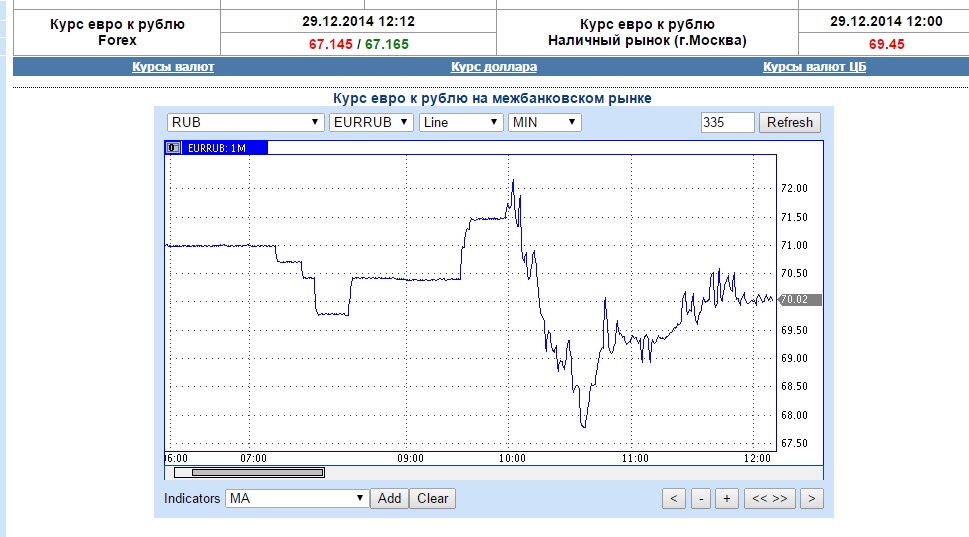 Хим. физ.
138 , 044320. (10.1063/1.4776758) [PubMed] [CrossRef] [Google Scholar]

48. Schuurman MS, Yarkony DR. 2007.
О приближении вибронной связи: общеприменимом подходе для определения полностью квадратичных квазидиабатических связанных гамильтонианов электронного состояния. Дж. Хим. физ.
127 , 094104. (10.1063/1.2756540) [PubMed] [CrossRef] [Google Scholar]

49. Plasser F, Ruckenbauer M, Mai S, Oppel M, Marquetand P, Gonzalez L. 2016.
Эффективное и гибкое вычисление многоэлектронных перекрытий волновых функций. Дж. Хим. Теория вычисл.
12 , 1207-1219. ( 10.1021/acs.jctc.5b01148) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

50. Plasser F, Gómez S, Menger MFSJ, Mai S, González L. 2019.
Высокоэффективная динамика поверхностных скачков с использованием модели линейной вибронной связи. физ. хим. хим. физ.
21 , 57-69. ( 10.1039/C8CP05662E) [PubMed] [CrossRef] [Google Scholar]

51. Raab A, Worth GA, Meyer HD, Cederbaum LS. 1998.
Молекулярная динамика пиразина после возбуждения в электронное состояние S2 с использованием реалистичного 24-модового модельного гамильтониана. Дж. Хим. физ.
110 , 936-946. ( 10.1063/1.478061) [CrossRef] [Google Scholar]

52. Унке О.Т., Чмиела С., Соседа Х.Е., Гастеггер М., Полтавский И., Шютт К.Т., Ткатченко А., Мюллер К.Р. 2021.
Силовые поля машинного обучения. хим. преп.
121 , 10 142-10 186 ( 10.1021/acs.chemrev.0c01111) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

53. Hu D, Xie Y, Li X, Li L, Lan З. 2018.
Включение поверхностей потенциальной энергии регрессии гребня ядра машинного обучения в оперативное моделирование неадиабатической молекулярной динамики. Дж. Физ. хим. лат.
9 , 2725-2732. ( 10.1021/acs.jpclett.8b00684) [PubMed] [CrossRef] [Google Scholar]

54. Chen WK, Liu XY, Fang WH, Dral PO, Cui G. 2018.
Глубокое обучение неадиабатической динамике возбужденного состояния. Дж. Физ. хим. лат.
9 , 6702-6708. ( 10.1021/acs.jpclett.8b03026) [PubMed] [CrossRef] [Google Scholar]

55. Westermayr J, Faber FA, Christensen AS, von Lilienfeld OA, Marquetand P. 2020.
Нейронные сети и регрессия гребня ядра для динамики возбужденных состояний CH ₂ NH ₂ ⁺ : от представлений с одним состоянием к представлениям с несколькими состояниями и моделей машинного обучения с несколькими свойствами. Мах. Учиться. науч. Технол.
1 , 025009. ( 10.1088/2632-2153/ab88d0) [CrossRef] [Google Scholar]

56. Унке О.Т., Мьювли М. 2019.
PhysNet: нейронная сеть для прогнозирования энергий, сил, дипольных моментов и частичных зарядов. Дж. Хим. Теория вычисл.
15 , 3678-3693. ( 10.1021/acs.jctc.9b00181) [PubMed] [CrossRef] [Google Scholar]

57. Dreuw A, Wormit M. 2015.
Алгебро-диаграммная схема построения пропагатора поляризации для расчета возбужденных состояний. ПРОВОДА: Комп.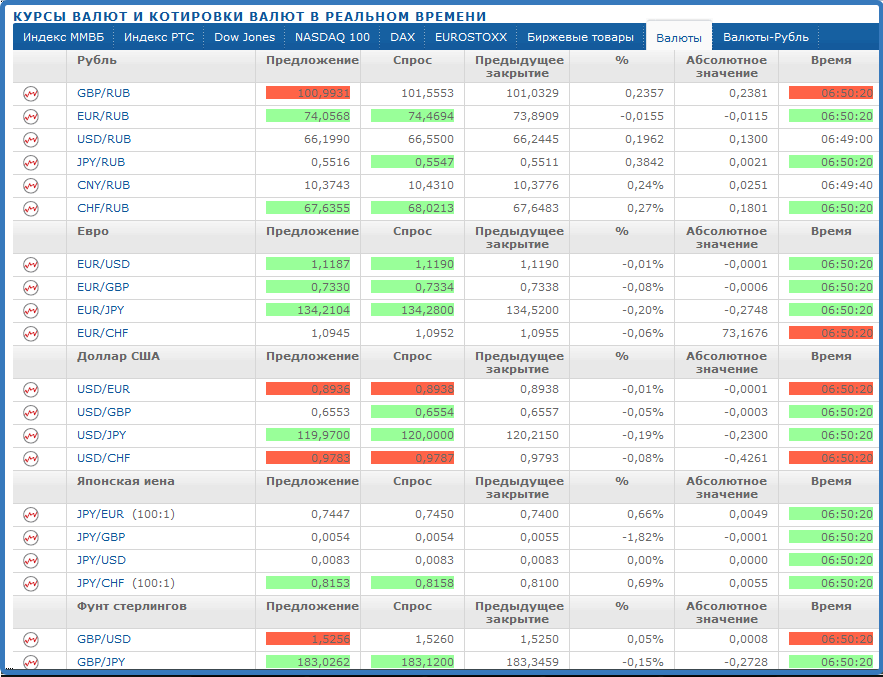 Мол. науч.
5 , 82-95. ( 10.1002/wcms.1206) [CrossRef] [Google Scholar]

58. Драл ПО, Гэ Ф, Сюэ Б-Х, Хоу Ю-Ф, Пинейро М., Хуан Дж., Барбатти М. 2021.
MLatom 2: интеграционная платформа для атомистического машинного обучения. Вершина. Курс. хим.
379 , 27. ( 10.1007/s41061-021-00339-5) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

59. Dral PO, Owens A, Yurchenko SN, Thiel W. 2017.
Выборка на основе структуры и самокорректирующееся машинное обучение для точных расчетов поверхностей потенциальной энергии и уровней вибрации. Дж. Хим. физ.
146 , 244108. ( 10.1063/1.4989536) [PubMed] [CrossRef] [Google Scholar]

60. Фонсека Г., Полтавский И., Василев-Галиндо В., Ткаченко А. 2021.
Улучшение молекулярных силовых полей в конфигурационном пространстве за счет сочетания контролируемого и неконтролируемого машинного обучения. Дж. Хим. физ.
154 , 124102. (10.1063/5.0035530) [PubMed] [CrossRef] [Google Scholar]

61. Botu V, Ramprasad R. 2015.
Адаптивная структура машинного обучения для ускорения молекулярной динамики ab initio. Междунар. J. Квантовая хим.
115 , 1074-1083. ( 10.1002/qua.24836) [CrossRef] [Google Scholar]

62. Смит Дж.С., Небген Б., Любберс Н., Исаев О., Ройтберг А.Е. 2018.
Чем меньше, тем лучше: выборка химического пространства с активным обучением. Дж. Хим. физ.
148 , 241733. (10.1063/1.5023802) [PubMed] [CrossRef] [Google Scholar]

63. Имбальцано Г., Чжуан И., Капил В., Росси К., Энгель Э.А., Грасселли Ф., Чериоти М. 2021.
Оценка неопределенности для молекулярной динамики и отбора проб. Дж. Хим. физ.
154 , 074102. (10.1063/5.0036522) [PubMed] [CrossRef] [Google Scholar]

64. Оделл А., Делин А., Йоханссон Б., Коквелл М.Дж., Никлассон AMN. 2011.
Геометрическое интегрирование в молекулярной динамике Борна-Оппенгеймера. Дж. Хим. физ.
135 , 224105. (10.1063/1.3660689) [PubMed] [CrossRef] [Google Scholar]

65. Swope WC, Andersen HC, Berens PH, Wilson KR. 1982.
Метод компьютерного моделирования для расчета констант равновесия для образования физических кластеров молекул — приложение к малым кластерам воды. Дж. Хим. физ.
76 , 637-649. ( 10.1063/1.442716) [CrossRef] [Google Scholar]

66. Hurd P, Cusati T, Persico M. 2010.
Интеграция траектории с разрывами потенциальной энергии. Дж. Вычисл. физ.
229 , 2109-2116. ( 10.1016/j.jcp.2009.11.025) [CrossRef] [Google Scholar]

67. Ву Сф, Маркус Р. 1970.
Аналитическая механика химических реакций. V. Применение к линейным реактивным системам H + h3. Дж. Хим. физ.
53 , 4026-4035. ( 10.1063/1.1673874) [CrossRef] [Google Scholar]

68. Трухлар Д.Г., Купперманн А. 1970.
Квантовая механика реакции H + h3: точные вероятности рассеяния при коллинеарных столкновениях. Дж. Хим. физ.
52 , 3841-3843. ( 10.1063/1.1673570) [CrossRef] [Google Scholar]

69. Guo Y, Thompson DL, Sewell TD. 1996.
Анализ проблемы нулевой энергии в классическом траекторном моделировании. Дж. Хим. физ.
104 , 576-582. ( 10.1063/1.470853) [CrossRef] [Google Scholar]

70. Wang H, Peslherbe GH, Hase WL. 1994.
Траекторные исследования нуклеофильного замещения SN2. 4. Внутримолекулярная и мономолекулярная динамика комплексов Cl—CH ₃ Br и ClCH ₃ —Br. Варенье. хим. соц.
116 , 9644-9651. ( 10.1021/ja00100a032) [CrossRef] [Google Scholar]

71. Bowman JM, Gazdy B, Sun Q. 1989.
Метод ограничения колебательной энергии в расчетах квазиклассических траекторий. Дж. Хим. физ.
91 , 2859-2862. ( 10.1063/1.456955) [CrossRef] [Google Scholar]

72. Миллер В.Х., Хасэ В.Л., Дарлинг С.Л. 1989.
Простая модель для исправления проблемы энергии нулевой точки в классическом моделировании траекторий многоатомных молекул. Дж. Хим. физ.
91 , 2863-2868. ( 10.1063/1.456956) [CrossRef] [Google Scholar]

73. Lim KF, McCormack DA. 1995.
Сохранение квантовых энергий нулевой точки в классическом траекторном моделировании. Дж. Хим. физ.
102 , 1705-1715. ( 10.1063/1.468697) [CrossRef] [Google Scholar]

74. Bonhommeau D, Truhlar DG. 2008.
Смешанное квантово-классическое исследование фотодиссоциации NH ₃ ( Ã ) и практический метод поддержания нулевой энергии в классических траекториях. Дж. Хим. физ.
129 , 014302. (10.1063/1.2943213) [PubMed] [CrossRef] [Google Scholar]

75. Varandas AJC, Marques JMC. 1994.
Метод квазиклассических расчетов траекторий на поверхностях потенциальной энергии, определяемых градиентами и гессианами, и модель для ограничения энергии в колебательных модах. Дж. Хим. физ.
100 , 1908-1920 гг. ( 10.1063/1.466544) [CrossRef] [Google Scholar]

76. Таунсенд Д., Лаханкар С.А., Ли С.К., Шамбро С.Д., Костюмы А.Г., Чжан Х, Райнекер Дж., Хардинг Л.Б., Боуман Дж.М. 2004.
Бродячий атом: отклонение от пути реакции при разложении формальдегида. Наука
306 , 1158-1161. ( 10.1126/science.1104386) [PubMed] [CrossRef] [Google Scholar]

77. Shepler BC, Braams BJ, Bowman JM. 2007.
Квазиклассические расчеты траектории диссоциации ацетальдегида на глобальной поверхности потенциальной энергии указывают на значительную динамику непереходного состояния. Дж. Физ. хим. А
111 , 8282-8285. ( 10.1021/jp074646q) [PubMed] [CrossRef] [Google Scholar]

78. Kurosaki Y. 2006.
Динамика потока энергии в молекулярном канале фотодиссоциации пропаналя C ₂ H ₅ CHO → C ₂ H ₆  + CO: прямое исследование молекулярной динамики ab initio. Дж. Физ. хим. А
110 , 11 230-11 236.( 10.1021/jp063452s) [PubMed] [CrossRef] [Google Scholar]

79. Shepler BC, Braams BJ, Bowman JM. 2008.
«Блуждающая» динамика в канале ₃ Фотодиссоциация CHO обнаружена на глобальной поверхности потенциальной энергии. Дж. Физ. хим. А
112 , 9344-9351. ( 10.1021/jp802331t) [PubMed] [CrossRef] [Google Scholar]

80. Xie Z, Bowman JM. 2006.
Энергетическое ограничение нулевой точки в квазиклассических расчетах траекторий. Дж. Физ. хим. А
110 , 5446-5449. ( 10.1021/jp055861e) [PubMed] [CrossRef] [Google Scholar]

81. Мукерджи С., Марио Б. 2022.
Бесгессеанский метод предотвращения нулевой утечки энергии в классическом моделировании траектории. ChemRxiv. ( 10.26434/chemrxiv-2022-53g43) [CrossRef] [Google Scholar]

82. Бек М.Х., Джекле А., Уорт Г.А., Мейер Х.Д. 2000.
Многоконфигурационный нестационарный метод Хартри (MCTDH): высокоэффективный алгоритм распространения волновых пакетов. физ. Респ.
324 , 1-105. ( 10.1016/S0370-1573(99)00047-2) [CrossRef] [Google Scholar]

83. Meyer H-D. 2012.
Изучение молекулярной квантовой динамики многоконфигурационным нестационарным методом Хартри. ПРОВОДА: Вычисл. Мол. науч.
2 , 351-374. ( 10.1002/wcms.87) [CrossRef] [Google Scholar]

84. Вендрель О., Мейер Х-Д. 2011.
Многослойный многоконфигурационный нестационарный метод Хартри: реализация и приложения к гамильтониану Хенона–Хейлса и пиразину. Дж. Хим. физ.
134 , 044135. (10.1063/1.3535541) [PubMed] [CrossRef] [Google Scholar]

85. Wang H, Thoss M. 2003.
Многослойная формулировка многоконфигурационной нестационарной теории Хартри. Дж. Хим. физ.
119 , 1289-1299. ( 10.1063/1.1580111) [PubMed] [CrossRef] [Google Scholar]

86. Манте У. 2008.
Многослойный многоконфигурационный зависящий от времени подход Хартри для квантовой динамики на общих поверхностях потенциальной энергии. Дж. Хим. физ.
128 , 164116. (10.1063/1.22) [PubMed] [CrossRef] [Google Scholar]

87. Englman R, Jortner J. 1970.
Закон энергетической щели для безызлучательных переходов в больших молекулах. Мол. физ.
18 , 145-164. ( 10.1080/00268977000100171) [CrossRef] [Google Scholar]

88. Subotnik JE, Ouyang W, Landry BR. 2013.
Можем ли мы вывести алгоритм Талли для скачков по поверхности из полуклассического квантового уравнения Лиувилля? Почти, но только с декогеренцией. Дж. Хим. физ.
139 , 214107. (10.1063/1.4829856) [PubMed] [CrossRef] [Google Scholar]

89. Уорт Г.А., Бек М.Х., Джекл А., Мейер Х.Д. 2019.
Пакет MCTDH, используемая версия: 8.4.18. См. http://Mctdh.Uni-Hd.De.

90. Уорт Г.А., Бек М.Х., Джекле А., Мейер Х.Д. 2019.
Пакет MCTDH, используемая версия: 8.5.10. См. http://Mctdh.Uni-Hd.De.

91. Талли Дж.К. 1990.
Молекулярная динамика с электронными переходами. Дж. Хим. физ.
93 , 1061-1071. ( 10.1063/1.459170) [CrossRef] [Google Scholar]

92. Грануччи Г., Персико М. 2007.
Критическая оценка алгоритма наименьшего количества переключений для скачкообразного перемещения по поверхности. Дж. Хим. физ.
126 , 134114. (10.1063/1.2715585) [PubMed] [CrossRef] [Google Scholar]

93. Баер М. 2006.
За гранью Оппенгеймера: электронные неадиабатические условия связи и конические пересечения. Хобокен, Нью-Джерси: John Wiley & Sons. [Google Scholar]

94. Köppel H. 2011.
Конические пересечения — теория, расчеты и эксперимент. В Diabatic represeantation: методы построения диабатических электронных состояний (ред. Domcke W, Yarkony DR, Köppel H), стр. 175-204. Сингапур: Мировой научный. [Академия Google]

95. Наскар К., Мукерджи С., Мукерджи Б., Рави С., Мукерджи С., Сардар С., Адхикари С. 2020.
ADT: обобщенный алгоритм и программа для уравнений Борна-Оппенгеймера размерного субгильбертова пространства « N ». Дж. Хим. Теория вычисл.
16 , 1666-1680. ( 10.1021/acs.jctc.9b00948) [PubMed] [CrossRef] [Google Scholar]

96. Barbatti M, Ruckenbauer M, Plasser F, Pittner J, Granucci G, Persico M, Lischka H. 2014.
Newton-X: программа прыжков по поверхности для неадиабатической молекулярной динамики. ПРОВОДА: Комп. Мол. науч.
4 , 26-33. ( 10.1002/wcms.1158) [CrossRef] [Google Scholar]

97. Барбатти М., Грануччи Г. , Персико М., Рукенбауэр М., Ваздар М., Эккерт-Максич М., Лишка Х. 2007.
Программная система Newton-X для прыжков по поверхности на лету: приложение для ab initio моделирования неадиабатической фотодинамики эталонных систем. Дж. Фотохим. Фотобиол. А
190 , 228-240. ( 10.1016/j.jphotochem.2006.12.008) [CrossRef] [Google Scholar]

98. do Casal MT, Toldo J, Pinheiro M Jr, & Barbatti M. 2021.
Наименьшее количество скачков по поверхности переключателей с муфтами Бэкана [версия 1; экспертная оценка: одобрено 3]. Открыть Рез. Евро.
1 , 49. (10.12688/openreseurope.13624.1) [CrossRef] [Google Scholar]

99. Poinot M. 2010.
Пять веских причин использовать иерархический формат данных. вычисл. науч. англ.
12 , 84-90. ( 10.1109/MCSE.2010.107) [CrossRef] [Google Scholar]

100. de Buyl P, Colberg PH, Höfling F. 2014.
H5MD: структурированный, эффективный и портативный формат файлов для молекулярных данных. вычисл. физ. коммун.
185 , 1546-1553. ( 10.1016/j.cpc.2014.01.018) [CrossRef] [Google Scholar]

101. Пинейро М. мл., Мукерджи С., Барбатти М. 2021.
Декартовы координаты 7-AIH ⁺ [Набор данных]. ( 10.6084/m9.figshare.14823126) [CrossRef]

102. Pinheiro M Jr, Mukherjee S, Barbatti M. 2021.
Данные о траекториях SBH [Набор данных]. ( 10.6084/m9.figshare.14873094) [CrossRef]

103. Мукерджи С. 2021.
Траектория DC-FSSH для режима 10D SBH [Набор данных]. Зенодо. ( 10.5281/zenodo.5039522) [CrossRef]

104. Сайкат М. 2021.
Данные моделирования MCTDH и ML-MCTDH для модели SBH [Набор данных]. ( 10,6084/м9.figshare.14869089) [CrossRef]

Отчет об удалении программы-вымогателя DarkBit

Программа-вымогатель базы данных угроз Программа-вымогатель DarkBit

По Mezo в программе-вымогателе

Программа-вымогатель DarkBit шифрует данные и требует выкуп за расшифровку. В процессе шифрования DarkBit изменяет имена затронутых файлов, переименовывая их со случайной строкой символов, за которой следует расширение «. Darkbit». Например, файл с исходным названием «1.jpg» будет отображаться как «5oCWq6Fp1676362581.Darkbit», а «2.png» — как «QV3xwMP11776363582.Darkbit» и так далее.

После завершения процесса шифрования DarkBit создает записку с требованием выкупа под названием «RECOVERY_DARKBIT.txt» и помещает ее на рабочий стол зараженной системы. В записке содержатся инструкции о том, как жертвы могут заплатить выкуп и получить ключ дешифрования, чтобы разблокировать свои зашифрованные файлы.

Требования DarkBit Ransomware

Записка DarkBit о выкупе начинается с политического или геополитического сообщения, подразумевающего, что программа-вымогатель нацелена на крупные организации, такие как компании, а не на домашних пользователей. Сообщение предупреждает жертв, что их файлы были зашифрованы с использованием надежного криптографического алгоритма AES-256, а конфиденциальные данные были собраны или украдены.

Примечание жертв предупреждает о том, что попытка использования сторонних инструментов или служб восстановления может привести к безвозвратной потере данных. Единственный способ восстановить зашифрованные файлы, по мнению злоумышленников, — это приобрести у них ключи или инструменты дешифрования. Требуемая сумма выкупа составляет 80 биткойнов (BTC), что по текущему обменному курсу биткойнов составляет около 1,7 миллиона долларов США. Следует отметить, что обменные курсы постоянно колеблются, и это преобразование может быть неточным.

Размер выкупа подтверждает предположение, что DarkBit обычно не используется для домашних пользователей. Если в течение 48 часов не будет предпринято никаких действий, сумма выкупа увеличивается на 30%, а через пять дней собранные данные будут выставлены на продажу.

Рекомендуемые действия после атаки таких угроз, как программа-вымогатель DarkBit

Основываясь на своем опыте анализа многочисленных заражений программами-вымогателями, специалисты по кибербезопасности обычно советуют не платить злоумышленникам любые суммы денег. В большинстве случаев расшифровка редко возможна без ключей или инструментов расшифровки, которыми обладают только злоумышленники. Некоторая расшифровка может быть возможна в случаях, когда программа-вымогатель имеет серьезные недостатки или все еще находится в разработке, но это скорее исключение, чем правило. Как и в случае любой атаки программ-вымогателей, жертвам рекомендуется сообщить об инциденте в правоохранительные органы и использовать надежное решение для кибербезопасности и защиты от вредоносных программ, чтобы удалить вредоносное ПО и предотвратить будущие атаки.

Записка с требованием выкупа, сброшенная программой-вымогателем DarkBit, гласит:

‘Уважаемые коллеги,
С сожалением сообщаем вам, что нам пришлось полностью взломать сеть Технион и перенести «все» данные на наши защищенные серверы.
Итак, сохраняйте спокойствие, переведите дух и подумайте о режиме апартеида, который вызывает проблемы то здесь, то там.
Они должны заплатить за свою ложь и преступления, свое имя и позор. Они должны заплатить за оккупацию, военные преступления против человечности,
убийств людей (не только тела палестинцев, но и души израильтян) и разрушение будущего и всех наших мечтаний.
Они должны платить за увольнение высококвалифицированных специалистов.

В любом случае, вам (как личности) не о чем беспокоиться.
Задача администрации выполнить нашу инструкцию по восстановлению сети.
Но вы можете связаться с нами через мессенджер TOX, если хотите восстановить свои файлы лично. (ID TOX: AB33BC51AFAC64D98226826E70B483593C81CB22E6A3B504F7A75348C38C862F00042F5245AC)

Наша инструкция для администрации:
Все ваши файлы зашифрованы с использованием алгоритма военного класса AES-256. Итак,

Не пытайтесь восстановить данные, потому что зашифрованные файлы невозможно восстановить, если у вас нет ключа.
Любая попытка восстановления данных без ключа (с использованием сторонних приложений/компаний) приводит к ПОСТОЯННОМУ повреждению. Отнеситесь к этому серьезно.

Вы должны доверять нам. Это наш бизнес (после увольнения из высокотехнологичных компаний) и репутация — это все, что у нас есть.

Все, что вам нужно сделать, это выполнить процедуру оплаты, после чего вы получите ключ расшифровки, который будет использоваться для возврата всех ваших файлов и виртуальных машин.