Анализ результатов торговли методом Монте-Карло и опасность недокапитализации. Метод монте карло биржа

Практикум для трейдера. Системный трейдинг

Оценка торговых систем методами Монте-Карло

Основная цель различных стресс-тестов - выявить слабые и наиболее уязвимые места в работе всех звеньев и, в общем смысле, определить вероятность провала. Моделирование методами Монте-Карло позволяет оценить устойчивость системы, чувствительность к входным параметрам и вероятность наступления конкретных сценариев развития. В этой статье я расскажу о нескольких способах применения Монте-Карло при оценке механических торговых систем.

"What is the last thing you do before you climb on a ladder? You shake it. And that is Monte Carlo simulation."

SamSavage, StanfordUniversity.

В последнее время все чаще можно услышать, что финансовые организации и банки периодически подвергаются различным стресс-тестам. Основная цель таких проверок - выявить слабые и наиболее уязвимые места в работе всех структур организации и, в общем смысле, определить вероятность банкротства.

Очень часто при этом применяется параметрический и вероятностный анализ математической модели всего бизнеса. Параметрический подход подразумевает под собой наличие входных параметров, от которых зависят интересующие аудитора показатели. Например, как прибыль кредитного отдела зависит от количества невозвращенных кредитов. Вероятностный анализ можно применять при работе с более сложными многопараметрическими моделями. Прогоняя по очереди большое количество различных параметров и их комбинаций, можно с большой достоверностью определить вероятность наступления событий, вплоть до самых неблагоприятных. Конечно, невозможно абсолютно точно рассчитать все возможные в реальности сценарии, но спрогнозировать вероятность убытков или чувствительность прибыли к входным параметрам можно с достаточно приемлемой достоверностью.

Возвращаясь к аналогии Сэма Сэведжа, скажу еще раз, что моделирование методами Монте-Карло позволяет оценить устойчивость системы, чувствительность к входным параметрам и вероятность наступления конкретных сценариев развития. В этой статье я расскажу о нескольких способах применения Монте-Карло при оценке механических торговых систем. Можно выделить три основных подхода:

1. Статистическая оценка математического ожидания торговой системы;

2. Моделирование линии эквити и последовательностей сделок;

3. Моделирование "истории" котировок.

В качестве примера я выбрал очень простую паттерновую шортовую торговую систему для фьючерса на индекс РТС. В основе этой системы лежит реализация очень краткосрочного стат.преимущества, открытая позиция держится ровно 30 минут. На рисунке можно посмотреть показатели эффективности стратегии на тестовом и вневыборочном интервалах:

При тестировании системы было заложено проскальзывание с хорошим запасом и, тем не менее, показатели средней эффективности сделок и вероятности прибыльного исхода остались на стабильно приемлемом уровне. Теперь перейдем непосредственно к моделированию.

СТАТИСТИЧЕСКАЯ ОЦЕНКА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ.

При этом подходе нам потребуется всего три показателя из базовой сводной таблицы. Это вероятность получения прибыли, средняя величина прибыльной сделки и средняя величина убытка. Важно, что эти величины нужно брать из столбца, соответствующего вневыборочному тестированию. В этом подходе результаты тестового периода имеют очень малую прогностическую ценность. Итак, имеем первые три входных параметра:

- вероятность прибыли = 57,69%, соответственно вероятность убытка = 1 - прибыль = 42,31%

- средняя прибыль = 0,73%

- средний убыток = -0,29%.

Теперь построим модель по методу Монте-Карло с использованием случайных чисел. Если выпавшее случайное число больше 0,4231 , то мы имеем прибыльную сделку в размере 0,73%. В противном случае мы имеем убыток в размере -0,29%. Сделаем последовательность из 192 сделок, чтобы сравнить результат моделирования с показателями тестового периода. Тут можно применить три варианта моделирования:

- чистое математическое моделирование. Это самый простой и примитивный метод моделирования "в лоб", когда используются фиксированные значения входных параметров математического ожидания сделок;

- "плавающее" моделирование базовых параметров. Этот метод моделирования использует случайные, нормально распределенные значения параметров. При этом среднее значение равно базовому, а стандартное отклонение равно 1/10 от базового. То есть вероятность прибыльного исхода будет "нормально" колебаться вокруг 0,5769 со стандартным отклонением в 0,0576. Этот вариант удобно применять для оценки наихудших сценариев, потому что можно посчитать вероятность события, когда процент и величина средней прибыли упадет, а величина среднего убытка вырастет;

- "плавающее" моделирование сделок. Самый реальный, но и наиболее ресурсоемкий вариант моделирования. Моделируется каждая сделка по отдельности с параметрами, аналогичными предыдущему варианту. То есть вероятность прибыли конкретной сделки является независимой случайной величиной, нормально распределенной вокруг базового значения в 57,69%. Точно так же пересчитывается средняя величина прибыли и убытка для каждой отдельной сделки.

На рисунке можно посмотреть различные варианты линий эквити и показатели тестирования при втором (левый столбик) и третьем (правый столбик) вариантах моделирования.

нажми на график для увелияения

На рисунке показаны распределения математического ожидания, прибыли после 192 сделок, максимальная серия убытков подряд и максимальная просадка. Поскольку это самый простой метод Монте-Карло моделирования, то некоторую предсказательную ценность имеют лишь оценки прибыли и максимальной серии убытков. Так, например, математическое ожидание сделки колеблется вокруг 0,3% , ожидаемая прибыль - 77-78%, максимальная серия убытков - 6. А вот ожидаемая просадка заметно занижена. В реальности прибыльные и убыточные сделки распределены гораздо менее равномерно, чем на этих графиках. Опытным путем можно использовать для первичной оценки удвоенное значение 99% доверительного интервала. Так, в нашем примере существует 1% вероятность того, что максимальная просадка превысит 3,85%. Значит для реальной оценки можно использовать значение в 7,7%.

Очень большое значение имеет число испытаний, которому подвергается модель при испытаниях. Разница в значениях, полученных при 50 и 100 прогонах, достаточно существенна. А вот при переходе от 10000 к 50000 изменяется лишь четвертая цифра после запятой, что уже в пределах статистической погрешности. Поэтому считаю, что 1000 испытаний - это критический минимум для получения достоверных результатов. Оптимально - не меньше 10000. В моем случае было проведено 100000 испытаний. Такое большое число позволяет оценить чувствительность модели к входным параметрам. В правом верхнем углу расположена таблица регрессионных коэффициентов для базовых параметров. Хорошо видно, что между вероятностью выигрыша, средним выигрышем и математическим ожиданием сделок существует прямая зависимость. Что, собственно, и следовало ожидать. Особый интерес вызывает конкретное соотношение этих самых зависимостей. Так, при этих значениях входных параметров, наибольшая зависимость от вероятности выигрыша. Чуть меньше эффективность системы зависит от средней величины выигрыша. И наименьший вес в устойчивости показателей придается средней величине проигрыша.

МОДЕЛИРОВАНИЕ ЛИНИИ ЭКВИТИ И ПОСЛЕДОВАТЕЛЬНОСТЕЙ СДЕЛОК

При этом подходе будет анализироваться последовательность сделок, полученных при тестировании торговой системы. Наиболее верным, опять же, будет использование сделок, полученных на вневыборочном интервале. Сейчас, в качестве образца, я сделаю некоторое упрощение и проведу анализ сделок с тестового периода. Торговая система практически не оптимизировалась, поэтому сделки с тестового периода можно признать в моем случае достаточно репрезентативными. Однако, более корректным и надежным, повторюсь, будет использование вневыборочных показателей. Можно выделить два основных варианта моделирования линий эквити:

- метод "случайная выборка сделок "без возвращения"". В этом случае сделки просто переставляются случайным образом, формируя новые серии. Количество сделок и, следовательно, конечный итог остается всегда одним и тем же. На рисунке этот подход изображен на левом графике и первом столбце;

- метод "случайная выборка сделок "с возвращением"". Более гибкий метод. Необходимо задать число сделок, и каждая сделка в полученной последовательности будет извлекаться случайным образом из базовой последовательности сделок. Сделки могут повторяться, поэтому этот вариант позволяет моделировать линии эквити любой требуемой длины. На рисунке этот подход изображен на правом графике. Второй столбец показывает результаты моделирования серии из 400 сделок, последний столбец - 192 сделки.

нажми на график для увелияения

Результаты моделирования гораздо более реалистичны по сравнению с методом моделирования МО:

- максимальная просадка колеблется от 6,9% при 192 сделках до 8,3% при 400 сделках;

- максимальная серия убытков - от 5 до 6 подряд;

- средняя ожидаемая прибыль - от 90 до 280%.

Примечательно, что ожидаемая прибыль растет с увеличением числа сделок быстрее, чем ожидаемая максимальная просадка. Аналогичные операции по Монте-Карло моделированию линии эквити и последовательностей сделок можно проделать в специальном приложении к программе Вэлс-Лаб. Достаточно загрузить в программу моделирования результаты тестирования стратегии и можно приступать к анализу вероятностей. Программа предоставляет те же два немного усложненных варианта моделирования: Монте-Карло анализ линии эквити и Бутстреп сделок. Основное отличие от моего метода "с возвращением" состоит в том, что программа имеет возможность сохранять допустимые серии и последовательности сделок и автокорреляций. Смотрим на результаты:

Верхняя часть показывает результаты "встряски" линии эквити. Этот метод предполагает случайную выборку «с возвращением», поэтому в последовательность сделки могут включаться несколько раз. Этим объясняется, что при постоянной длине последовательности, итоговая прибыль может варьироваться. Нижняя часть показывает результаты Бутстрепа сделок. Сравним с моими показателями:

- 90% доверительный интервал просадки составляет от 3,32% до 11,2%, по сравнению с моими 3,94-11,3%

- Максимальная серия убытков в программе не считается. Зато можем посмотреть вероятность безубыточности, которая составляет 99,83%.

МОДЕЛИРОВАНИЕ "ИСТОРИИ" КОТИРОВОК.

Самый интересный и наименее изученный метод. В чистом виде не анализирует параметры торговой системы, а моделирует "окружающую среду". Этот метод построен на предположении, что "история повторяется, но в другом виде". Для моделирования потребуется рассчитать приращения каждого бара рабочего таймфрейма, после чего эти бары тщательно перемешать и сгенерировать новую "историю". Главной задачей в этом подходе является выбор алгоритма по расчетам новых баров. Проанализировав несколько подходов, я остановился на достаточно простых способах расчета максимальных и минимальных значений:

- открытие, максимум, минимум и закрытие бара расчитываются по отношению к значению предыдущего закрытия;

- открытие и закрытие бара расчитываются по отношению к предыдущему значению, а максимум и минимум - по отношению к текущему закрытию;

http://www.russian-trader.ru/article...ntekarlo/5.png

Оба метода позволяют генерировать достаточно качественные "истории". Я остановился на втором методе, так как он имхо более правдоподобно отражает волатильность текущего бара. При тестировании будут использованы оба подхода:

- генерация истории "без возвращения", на итоговом рисунке результаты тестирования представлены в верхней части, а сводная таблица помечена как "Монте-Карло".

- генерация истории "с возвращением", на итоговом рисунке снизу, таблица помечена как "Бутстреп". Этот подход позволяет генерировать "истории" любой длины, поэтому было протестирована 1000 различных вариантов длиной от 1/2 до 4 длин базовой истории.

Поскольку генерация "с возвращением" допускает использование одних и тех же баров по нескольку раз, то необходимо проверить распределение приращений, полученных в новой истории:

Приращение вполне рыночное, лапласовское, с длинными хвостами, поэтому можно говорить о приемлемости этого метода генерации "историй". Теоретически, подобное моделирование может в корне изменить структуру рынка и торгуемых паттернов, поэтому требуют дополнительного анализа и пока являются индикативными. С другой стороны, рынок в будущем вполне может принять форму подобных генераций, так как построена она с нормальной логикой и реальными исходными данными. Пока не доказано обратное, результаты такого моделирования при большом количестве проходов вполне могут выявить подгонку параметров торговой системы под конкретный график. Итак, смотрим результаты тестирования системы на новых "историях":

нажми на график для увелияения

Результаты можно признать позитивными. Средняя прибыль на сделку составляет 0,08-0,09%, средняя просадка - 19%, средняя вероятность выигрыша - 48%. Хорошо видно, что метод "с возвращением" дает более широкий разброс значений. Однозначно, это очень перспективный и требующий более тщательного изучения метод моделирования.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Поскольку я уже успел получить вопросы по технике автоматического построения выборок в Экселе, то остановлюсь на этом вопросе более подробно. Сделки извлекаются из общего массива сделок функцией ИНДЕКС(). Основной задачей является определение "случайности" номера строки, из которой будет браться сделка для новой последовательности.

- выборка "с возвращением". Берется случайное число и нормируется в диапазон ( 1 ; исходное число сделок ), после чего берется только целая часть при помощи функции ЦЕЛОЕ(). Получаем случайный номер сделки, которую и подаем в функцию ИНДЕКС().

- выборка "без возвращения". Берется ряд случайных чисел, ранжируется по порядку и каждому числу присваивается порядковый номер. Вся эта операция делается автоматически при помощи функции РАНГ(). Потом из массива сделок извлекается сделка под номером, соответствующим порядковому номеру случайного числа.

Таким образом, мы получили автоматическую генерацию последовательности, которую можно в дальнейшем анализировать при моделировании линии эквити и последовательностей сделок. Эта последовательность будет автоматически перекомбинироваться при каждом пересчете или по нажатиии клавиши F9. На рисунке эти методы представлены более подробно с необходимыми столбцами случайных чисел, требуемыми формулами для автоматических перестановок и графиками полученных линий эквити:

нажми на график для увелияения

В КАЧЕСТВЕ ЗАКЛЮЧЕНИЯ

В качестве первичной оценки можно рекомендовать метод статистического анализа путем "плавающего" моделирования базовых параметров. Это очень простой способ измерить устойчивость торговой системы и чувствительность ко входным параметрам. Вторым этапом в анализе МТС можно рекомендовать моделирование вневыборочных последовательностей сделок методом "с возвращением". Это позволит более качественно оценить величину максимальной просадки. И, наконец, оценить степень подгонки входных параметров торговой системы позволит метод моделирования "историй" котировок.

В этой статье я рассказал о некоторых способах оценки готовой торговой системы. Эти способы моделирования не помогут непосредственно в разработке торговых стратегий, они предназначены для нахождения пределов прочности и устойчивости. Большинство операций проводились в Экселе при помощи программы параметрического моделирования и оценки рисков. Проведя несколько тысяч испытаний можно с некоторой достоверностью оценить потенциальную прибыль, просадку, серию убытков и любые другие нужные пользователю показатели. Очень часто это может понадобиться при принятии таких решений, как отказываться или нет от системы, если она неожиданно дает несколько убытков подряд. Безусловно, Монте-Карло моделирование лишь инструмент для работы с математической моделью. Поэтому качество результатов напрямую зависит от качества анализируемой торговой системы. Использование вневыборочных показателей способно немного нивелировать ошибки плохих или переподогнанных систем, но большое внимание нужно уделять созданию устойчивой системы еще на этапе ее разработки.

Тарас Правдюк

Русский Трейдер

fxtreder.ru

Анализ результатов торговли методом Монте-Карло и опасность недокапитализации

Тут на днях некие участники смарт-лаба с удивлением обнаружили, что даже наличие торговой системы с положительным матожиданием не гарантирует получения прибыли и даже иногда приводит к потере счета. Впали в депрессию...

Что самое интересное — это правда. Но основная причина, кторая приводит к сливу депозита — это недокапитализация трейдера, или, проще говоря — недостаток бабла. Сколько людям не говорят, что $2K это недостаточно для торговли мини контрактами на CME, только микро — но не верят. Как нельзя с 15Круб торговать фьючем РТС — не верят. В результате — слитые счета и вера в кукла. А сколько достаточно? Можно рассчитать с помощью файла excel, который моделирует методом Монте-Карло вероятные результаты вашей торговли за один год. Файл лежит тут: yadi.sk/d/YlYHyHil4ay0W

Анализ результатов торговли методом Монте-Карло и опасность недокапитализации

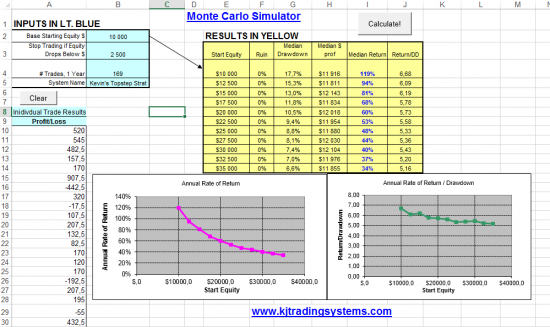
В ячейке B2 (Base Starting Equity $) вводите размер капитала, которым Вы располагаете для торговли. В ячейке B3 (Stop Trading if Equity Drops Below $) указывате ваш стопаут по счету, т.е. сумма, при падении до которой цены портфеля вы заканчиваете с торговлей и идете на завод вертеть гайки. В ячейку B4 (# Trades, 1 Year) заносите общее количество сделок за год, а в ячейку ниже можно записать название вашей торговой системы.

После чего удаляете все значения в столбце «A» с 10 строки и ниже, и заменяете их результатами индивидуальных сделок по вашей системе. Чем их больше, тем резултат точнее, но при большом количестве данных расчет может занять много времени.

Жмете на кнопку «Calculate!». Наслаждаетесть результатом. В желтой табличке колонка Ruin показывает вероятность слива счета в течении года в зависимости от размера начального капитала. Если в чем не разберетесть — можете спростиь в комментах. Удачи!

smart-lab.ru

Метод Монте Карло в трейдинге - 2018-03-01

Каждый трейдер стремится к тому, чтобы его торговля была успешной и приносила постоянный доход. Но каким образом можно отследить эффективность своей торговой системы и посмотреть, как лучше всего ее оптимизировать? В интернете довольно много советов, как улучшить стратегию, однако все это лишь субъективные рекомендации, которые могут подойти одному трейдеру и не подойти другому. Часто рассуждения о прибыльности торговли сводятся исключительно к психологическим аспектам, но если вы хотите точных цифр и четких указаний, то вам на помощь придет метод математического моделирования, или метод Монте Карло.

Чтобы использовать этот метод, нужно условиться, что торговля осуществляется с учетом постоянного риска, то есть, в каждой сделке у вас есть определенный процент, который вы можете потерять. Предположим, что вы каждый раз выставляете одинаковые значения стоп-лосса и тейк-профита по всем своим позициям, следовательно, вы либо теряете каждый раз N процентов от депозита, либо приобретаете столько же, если каждая сделка будет закрываться по стоп-ордеру. Конечно, это очень упрощенная схема трейдинга, но она понадобится нам, чтобы продемонстрировать принцип Монте Карло легко и быстро. Есть также варианты расчета и для переменных стоп-ордеров, но они намного сложнее.

Метод Монте Карло: описание

Этот метод также называется «метод статистических испытаний», и его суть в том, что компьютер автоматически формирует историю изменения вашего торгового баланса, случайно разыгрывая сделки и усредняя результаты. На основании этих действий вы получите вероятность наступления тех или иных событий в торговле. Почему компьютер выбирает сделки случайно, если вы торгуете систематически? Дело в том, что какой бы ни была ваша торговля, она всегда является случайной с точки зрения математического ожидания, и исход каждой вашей сделки нельзя заранее предсказать. Иными словами, для математического расчета последовательность ваших торговых действий не так важна, и метод предполагает беспристрастные расчеты, которые применимы не только для ваших исторических котировок.

Как же работает Монте Карло алгоритм?

Успешные трейдеры демонстрируют примерно одинаковый процент прибыльных сделок (50-75%), но обычно такую величину спрогнозировать довольно сложно, поэтому она будет являться переменной (Х). Для расчета также понадобятся три других параметра:

Т — то, во сколько раз вы планируете приумножить свой первоначальный депозит
N — максимальное число сделок, чтобы достичь приумножения депозита
Р — максимальная просадка в торговле

Итак, задача такова: каков оптимальный риск (R) допустим, чтобы увеличить депозит T за N-ное количество сделок и с просадкой депозита не более Р процентов. Если вручную такое вычисление произвести довольно сложно, то компьютер, используя алгоритм Монте-Карло, сделает это за считанные минуты. На экране вы увидите графики, на которых показана вероятность успеха в зависимости от риска, и сможете посмотреть, каким процентом депозита вы можете позволить себе рисковать при каждой сделке.

Метод Монте Карло: пример

На каждом графике Монте-Карло изображены максимумы и минимумы прибыльности при тех или иных значениях риска, а также область оптимального риска. Например, если есть 4 значения доли успешных сделок (50% при торговле наугад, 55%, 60% и 70% при условии торговли по стратегии), то получится 4 кривые линии. Допустим, у всех них максимум риска в районе 3-5%, а серым вертикальным прямоугольником обозначен оптимальный риск — например, от 3 до 5 процентов.

Максимум риска — это область, где увеличивается вероятность большой просадки депозита, а минимум риска — это тот уровень, при котором вам может не хватить выбранного количества сделок для того, чтобы увеличить депозит до задуманного значения. Допустим, при риске 6% вы можете слиться, а при риске 1% вы, вероятно, не сможете так быстро нарастить баланс торгового счета.

Анализ Монте Карло поможет вам с математической точностью рассчитать, какие показатели торговли нужны для вашей торговой стратегии и добиться высокой эффективности трейдинга.

Читайте также: Мастер-класс от «волков с Уолл-стрит»: как правильно выстроить свою деятельность на финансовом рынке?Hard fork Bitcoin: успехи, неудачи и перспективыБездепозитные бонусы Форекс брокеров - 2018: сравниваем и выбираемBitcoin Diamond криптовалюта — обзор форка БиткоинаNuBits (NBT) — особенности майнинга криптовалюты

ratingfx.ru

Расчет премии по опциону методом Монте-Карло vs формула Блэка-Шоулза / Хабр

Проблематика вопроса сформулирована в предыдущей статье.

А именно: как оценить влияние определенного допущения модели Блэка-Шоулза на расчетную величину премии по европейскому опциону? Допущения о том, что цена торгуемого актива имеет логнормальное распределение. Как альтернативу расчета по формуле Блэка-Шоулза я использовал подход — прогнозирование выплат покупателю опциона методом Монте-Карло. На вход программе я подавал:

“эталонные данные” (моделирование логнормального распределения”),
случайный ряд, характеризующийся распределением с “толстыми хвостами”,
и, наконец, цены нескольких биржевых активов — валютных пар и криптовалют.

В каждом случае я рассчитал премию опциона по формуле Б-Ш и методом Монте-Карло. Сравнил результаты и сделал(?) выводы:

Ранее я построил в MS Excel два гипотетических ценовых ряда: ABS/USD — ценовой ряд, описываемый логнормальным законом распределения. И серию WRD/USD — ценовой ряд, распределение которого характеризуется большей вероятностью меньших изменений при существенной вероятности больших (> 3σ) изменений.

Коэффициенты в таблице Excel были подобраны так, чтобы оба этих виртуальных ценовых активов характеризовались одинаковой величиной HV. При таких условиях и равных параметрах опционного контракта (текущая цена, страйк, экспирация) расчет премии по опциону ABS/USD и WRD/USD по формуле Блэка-Шоулза даст одно и то же значение для обоих активов.

Альтернативный способ оценить размер премии — моделировать выплаты по опциону методом Монте-Карло. Провести ряд итераций, на каждой итерации моделируя цену на N дней вперед. В конце итерации посчитать прибыль покупателя опциона.

“Справедливая” премия по опционному контракту будет нами получена, как сумма выплат, деленная на количество итераций. Вопрос: совпадет ли премия, рассчитанная таким способом (программно) с премией, рассчитанной по формуле Б-Ш?

Ну и, наконец, я собираюсь применить ту же методику оценки премии для исторических данных реальных биржевых активов. Нескольких валют и криптовалют, торгуемых за другие валюты и криптовалюты.

В следующей таблице я рассчитал цену WRD/USD (распределение цены имеет “толстые хвосты”) несколько раз подряд на 30 дней вперед. Как и прежде, цена WRD/USD изменялась каждый день в $inline$ раз.

В 2-х случаях из 5 цена актива WRD/USD выросла, в 3-х случаях — упала:

Соответственно, в 2-х случаях покупатель CALL-опциона смог реализовать прибыль, равную (1027.70 — 1000) + (1046.92 — 1000) = $74.62.

Делим $74.62 на количество возможных исходов (5) и получаем премию, что составит $14.92. Несколько больше, чем дал нам предыдущий расчет методом Б-Ш. Но так и метод наш не очень точен: всего 5 итераций.

Программное моделирование покупки опциона

На этом этапе Excel нам уже недостаточно. Я провел 5 имитационных экспериментов: заполнил 5 столбцов сгенерированной для нашего гипотетического актива WRD/USD ценой. Но для нашей цели — хорошей сходимости оценки премии по опциону — не хватит и 500 экспериментов.

Кроме того, как мы помним, цена WRD/USD — функция от СВ с функцией плотности — суммой функций плотности двух нормальных распределений. Случайная последовательность, подчиняющаяся закону распределения, измысленному мной в качестве примера. С параметрами, подобранными исключительно в целях демонстрации, но не отражающими динамику цен какого-либо реального товара. Это совсем не то, что нам потребуется для анализа биржевого актива. Нам нужна программа, реализующая логику вида:

Логика программы на высоком уровне:

1) прочитать из источника (файла) исходный ценовой ряд
2) провести предварительную обработку ценовых данных
3) построить таблицу кумулятивной функции распределения исходного ценового ряда
4) используя таблицу, полученную на шаге выше, и генератор равномерно распределенной СВ, провести N экспериментов:
4.1) в каждом эксперименте рассчитать M последовательных (автокоррелированных) цен
4.2) вычислить прибыль покупателя опциона — разность последней цены и страйк цены. Для Put-опциона разность берется с обратным знаком
5) сложить прибыль покупателя, полученную на каждом из N шагов и поделить результат на N

Устранение тренда

В простом алгоритме, приведенном выше, один пункт требует объяснений: “предварительная обработка ценовых данных”. Поясню на примере графика цены актива ABS/USD (распределение цены — логнормальное), полученного нами ранее:

конечная цена актива ABS/USD ниже исходной цены. Нисходящий тренд нашего актива — не закономерность, но влияние недетерминированного фактора — напомню, мы использовали генератор случайных чисел.

В то же время, про актив ABS/USD априори известно, что его цена, в общем случае, дрейфует равновероятно вверх либо вниз. То есть, в модели математическое ожидание отклонения цены ABS/USD равно 0.

В статистической оценке математическое ожидание — среднее значение ценового изменения — получилось отрицательным.

Корректно ли использовать для расчетов данные, в которые уже заложено априорное “знание” об отрицательной доходности актива? Слово “знание” неспроста забрано в кавычки: мы знаем, что актив ABS/USD имеет равную вероятность как вырасти в цене, так и подешеветь. Такова модель данных, использованная нами в расчете.

С другой стороны, статистика показывает нам отрицательное математическое ожидание дневной ценовой динамики. И это “знание”, полученное на, по сути, случайной, выборке, мы заложим в модель.

ABS/USD — актив гипотетический. Совершенно определенно можно сказать, что, для построения таблицы — функции распределения, что впоследствии будет использована для генерации ценовых прогнозов, имеющийся тренд — статистическая ошибка, которую необходимо устранить.

Но что если мы анализируем реальный рыночный актив? Не ABS/USD, а, например, EUR/USD? Как быть с трендом, имевшим место в действительности?

Мое мнение: из истории цен тренд необходимо убрать. Обратное справедливо, если у нас есть «достоверные» данные о том, что цена актива продолжит снижение в будущем. Да, есть такие валюты, товары и прочие объекты торговли, на динамику ценообразования которых экономический анализ дает определенный прогноз. Чего нельзя сказать, например, о большинстве криптовалют.

Там, где достаточно аргументированных высказываний как в пользу восходящего, так и в пользу нисходящего тренда, исторические цены должны быть “выровнены”:

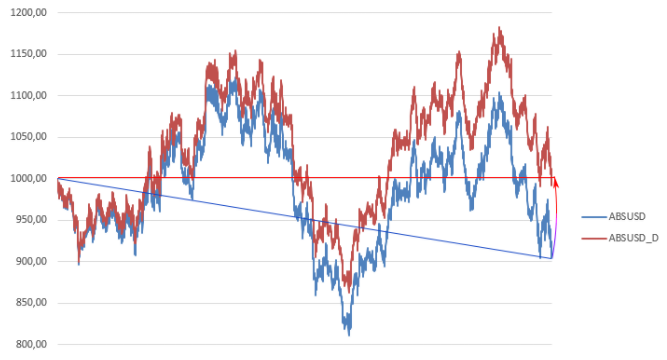
На рисунке исходная синяя кривая была скорректирована: из каждого i-го значения цены вычтена величина, равная i*d, где d равна разнице первой и последних цен, деленной на количество временных отрезков (количество цен минус 1).

В прикладной программе, предназначенной для оценки величины премии по опционному контракту, вероятно стоит предусмотреть два варианта расчета: с устранением тренда и с данными, взятыми и использованными, как есть.

Определенно, там, где у нас нет полной уверенности в динамике цен на прогнозируемый период, тренд следует устранить. А если уверенность есть — стоит ли тратить время на изучение деривативов, когда можно просто выйти на рынок со всеми доступными средствами, и, с ощутимой выгодой, монетизировать свои прогнозы?

Еще замечание: тренд необязательно устранять непосредственно из цен. К примеру, биткойн с его ростом более чем на сто процентов за один только год после удаления из цен трендовой составляющей вообще зайдет в отрицательную полуплоскость по оси цены. Отрицательная цена, определенно, не годится для дальнейших расчетов. Альтернатива, которой я и воспользуюсь — удалить тренд из ряда ценовых изменений — $ln(\frac{x_i}{x_{i-1}})$ , где $x_i и x_{i-1}xi$ — текущее и предыдущее значение цен.

Построение и использование обратной кумулятивной функции распределения

В программе, что я приведу в депозитарии кода github по ссылке, пожалуй, самая “интеллектуальная” часть — это построение обратной кумулятивной (интегральной) функции распределения и использования ее для генерации случайного ценового приращения. Весь процесс разбит на несколько шагов.

На первом шаге я получаю из цен $inline$ приращения $d_1, d_2, …, d_{N-1}: d_i = ln(\frac{x_i}{x_{i-1}})$

Далее, если выбрана опция устранения тренда, я получаю новый ряд приращений цен, вычитая из каждого значения $inline$ величину, равную $\frac{d_{N-1}-d_1}{N-2}$ . Значения приращений цены я сортирую по возрастанию.

Процесс построения обратной функции распределения реализован в одном цикле. Представим, что цена изменяется ( $x_{i+1}=x_i*e^{d_i}$ ) на дискретные значения $inline$ . Какова вероятность, что цена изменится в $e^{d_1}$ или меньше раз, где $inline$ — наименьшее из значений приращения цены в нашей выборке? Очевидно, вероятность эта составит $\frac{1}{N-1}$ . Какова вероятность того, что цена изменится в $e^{d_2}$ или менее раз? Очевидно, эта вероятность равна сумме вероятностей двух несвязанных исходов: изменения цены в $e^{d_1}$ раз либо в $e^{d_2}$ раза, или же $\frac{1+1}{N-1}$ .

Т.е., имея отсортированный ряд $d_1, d_2, …, d_{N-1}$ , нам достаточно построить из него ряд кортежей

$[d_1, \frac{1}{N-1}], [d_2, \frac{2}{N-1}], … [d_{N-1}, \frac{N-1}{N-1}]$

Итак, обратная функция построена. Как нам получить “случайное” значение изменения цены, используя таблицу и генератор равномерно распределенных случайных чисел? Примерно так же, как мы это делали в Excel.

К примеру, моя таблица содержит 500 записей вида:

Вероятность, P	Дельта, D
0.002	-0.0172
0.004	-0.0699
...	...

В построенной программой таблице 1-я записи соответствует вероятность, равная 1 / 500, второй — 2 / 500 и так далее.

Я получаю случайное дробное число в диапазоне от 0 до 1. К примеру, 0.269. Умножаю случайное число на количество записей в таблице (500): 0.269 * 500 = 134.5. Нужное мне значение дельты будет “посередине” между 134-й и 135-й строкой таблицы:

$D_{134} + (D_{135} - D_{134})*(134.5 - 134.0)$

Как только мы интерполировали значение приращения цены, мы вычисляем новое значение цены по формуле

$p_{i+1} = p_i * e^D$

Результаты моделирования

Сейчас моя задача — верифицировать алгоритм расчета премии по опциону с использованием алгоритма, описанного выше. Верифицировать на примере расчета, проведенного для активов ABSUSD (логнормальный) и WRDUSD (толстохвостый). Напомню: ABSUSD характеризуется приращениями цен, имеющими логнормальное распределение. То самое распределение, что предполагает модель Б-Ш. Актив WRDUSD демонстрирует динамику цен, более близкую к реальному рынку.

В программе я указал ровно те же параметры, что и для расчетов в Excel. Вместо вычисления премии по формуле, использующей стандартное отклонение, на вход программе я передал ценовые временные ряды наших активов. Результат демонстрирует таблица:

-	ABS/USD	WRD/USD
закон распределения цен	логнормальное распределение	“реальное” распределение
премия по формуле Б-Ш	10.80	10.80
премия, полученная в результате моделирования динамики цен	10.70	11.20

Расчет для актива ABS/USD дает практически тот же результат, что и формула Б-Ш. А вот для актива WRD/USD “моделированная” премия уже заметно отличается от результата аналитического расчета.

Причин тому может быть две: сама природа ценового ряда WRD/USD и / или ошибка выборки.

Мы должны быть уверены, что различие в результатах моделирования и аналитического расчета обусловлено именно природой нашего виртуального актива. С этой целью я проведу 10 итераций расчета премии, сгенерировав 10 рядов цен WRD/USD. Для каждой такой выборки посчитаю стандартное отклонение, подставлю его в формулу Б-Ш и получу результат аналитического расчета:

Можно сказать, что ошибка выборки в большей степени повлияла на результат расчета программы, чем на результат вычислений по формуле Б-Ш. В ходе 10 экспериментов были получены средние значения размера премии:

программный результат: 11.0,
по формуле Б-Ш: 10.83.

Различия в результате незначительны. Из чего можно сделать вывод: до сих пор значительного влияния закона распределения цен на оценочное значение “справедливой” премии по опционному контракту мне обнаружить не удалось.

Расчет премии по рыночным контрактам

До сих пор мы анализировали “виртуальные” активы, динамика которых подчиняется законам, нами же и сформулированными. Цель же настоящих изысканий — оценить реальные активы. Опционные контракты на криптовалюты, стоимость которых выражена в фиатных валютах либо других криптовалютах.

Как и раньше, возьмем ванильный 30-дневный опцион BTCUSD — курс Bitcoin к доллару США. Проведем 4 итерации расчета. Для первой итерации в качестве входных данных возьмем всю историю котирования BTCUSD, с 2011 по 2017 год. Посчитаем премию, устранив тренд из исходных данных. Текущей ценой примем $10 709 за 1 биткойн.

Премия, полученная аналитически (Б-Ш), составила $1234. Моделированием ценового ряда в программе получаем величину премии $1938. Расхождение аналитического результата с программным в случае BTCUSD на сей раз значительное.

В качестве исходных данных мы взяли всю историю котирования биткойна. Вообще, при расчете премии по опциону принято брать не все имеющиеся данные, но относительно “свежую” историю цен. Тот же биткойн прошел через череду взлетов и обвалов цен, характерную для развивающегося, “незрелого” рынка.

Очевидно, было бы странно строить оценку стоимости опциона сегодняшнего популярного и ликвидного актива, отталкиваясь от истории 7-летней давности, когда биткойн был диковинкой, а капитализация его была ничтожна.

Биткойн образца 2011 года и биткойн нынешний, с точки зрения финансового мира — два разных актива. Потому я повторю расчеты, ограничившись периодом 2014 — 2017 гг, затем периодом 2016 — 2017 год:

-	HV, %	Премия (программа)	Премия (Б-Ш)
2011-2017	101.15	1938.34	1234.67
2014-2017	66.26	1127.22	810.40
2016-2017	62.96	1407.93	770.15

Чему можно приписать такое значительное расхождение премии, рассчитанной двумя способами? Ошибке выборки или же плохой применимости формулы Б-Ш для волатильного, “непредсказуемого” криптоактива?

Для сравнения, приведу данные по расчету премии опционов на популярные валютные пары / золото:

Для “зрелых” рынков, как видно из таблицы, расхождения в результатах моделирования с формулой Б-Ш не столь значительны, как для BTCUSD (биткойна).

Следующая диаграмма показывает, как различаются рассчитанные значения премии (программа / формула Б-Ш) для фиатных валют, золота и криптовалют:

Насколько надежна Ваша стратегия? Введение в метод Монте-Карло.

Метод Монте-Карло (или моделирование) является статистической техникой, основанной на использовании торговых операций в качестве вспомогательного механизма для наиболее реалистичной оценки рисков и рентабельности Вашей торговой стратегии.

Неопределенность прогнозирования будущих результатов Торговых операций

Исторические результаты торговой стратегии свидетельствуют о том, как проявляла себя стратегия в прошлом. При прогнозировании рентабельности стратегии в будущем, мы сталкиваемся с неопределенностью. Для нас не важен доступный объем исторической информации, так как мы не можем с уверенностью сказать, что ждет нас в будущем. Мы можем лишь подготовить оценку, основанную на исторических результатах, опыте, накопленном нами в данной области, или на опыте, который имелся у нас в прошлом. Несмотря на то, что нам пригодится данная оценка, мы не можем узнать, насколько прогноз будет соответствовать реальным результатам в будущем.

Моделирование Монте-Карло (МК) позволяет нам получить вероятностную интерпретацию нашего прогноза. Вкратце, результаты моделирования Монте-Карло предлагают нам данные о предполагаемой и основанной на статистике рентабельности торговой стратегии. Моделирование может помочь Вам принять решение о надежности Вашей стратегии, о соотношении прибыль/максимальный убыток, ожидаемом для Вашей стратегии, а также о целесообразности применения стратегии или полного отказа от нее.

Что представляет собой метод Монте-Карло?

В рамках моделирования Монте-Карло предлагается список моделей возможных результатов с рандомизацией параметров модели в соответствии с заданным распределением вероятностей. Затем, несколько раз осуществляется подсчет результатов, в зависимости от использования различных комплексов случайных значений модели.

Самое простое объяснение заключается в том, что метод Монте-Карло основан на выполнении одного и того же моделирования несколько раз, при каждом случае возникновения незначительных случайных изменений. Чем больше число повторений, тем выше статистическая достоверность результатов.

Пример использования Метода МК – Изменение последовательности операций

Историческим обоснованием является простой список операций. Что в нем можно рандомизировать? Например, последовательность операций. Порядок операций, осуществленных в прошлом, является относительно случайным. В случае если рентабельность системы составляет 60%, Вы имеете основания ожидать, что 60% операций будут рентабельными, а 40% убыточными, но Вы не можете сделать вывод о том, в какой последовательности они будут происходить.

Просто после перетасовки поступлений, Ваша окончательная выручка будет той же самой, но максимальные убытки могут в значительной степени измениться. Вместо 10% сокращения Вы можете столкнуться с сокращением в размере 30%, исключительно изменив порядок проведения операций. Таким образом, какому значению следует доверять? Чего следует ожидать в будущем?

Ответ кроется в статистике, это основа метода Монте-Карло. Вы можете позволить программе выполнить данную реорганизацию 100 раз и увидите, каковым будет наибольшее и наименьшее сокращение, достигнутое в ходе случайных изменений.

На рисунке 1 изложена система. На рисунке 3 представлены 100 различных действий, выполненных с использованием той же системы. Все, что мы сделали – изменили последовательность операций.

Как рассчитываются эти значения?

Очень просто. Первая строка представляет результат первоначальной стратегии, остальные – уровни доверия (или вероятности), рассчитанные с использованием метода Монте-Карло. Номера слева являются уровнями доверия, которые показывают нам, с какой степенью доверия (вероятности) мы можем ожидать, что результаты останутся теми же или будут лучше, чем указано в соответствующей строке.

Например, значения на уровне доверия 95% означают, что в рамках 100 случайных выполненных нами моделирований, 95 из них (95%) обладали теми же или лучшими значениями, чем значения на уровне доверия.

Или, другими словами, вероятность, что максимальные убытки составят более 30,07%, не превышает 5%. Значение, равное 95%, является обычным рассматриваемым уровнем доверия. Вы можете реально ожидать, что результаты системы будут теми же или лучшими по сравнению со значениями данного уровня доверия.

Какие характеристики могут выступать в качестве случайных в рамках метода Монте-Карло?

Когда мы работаем с историческими результатами трейдеров, список выполненных в прошлом операций – это все, что у нас есть. Так что мы можем с ними сделать?

1. Изменить порядок осуществления операций. Существует 2 возможности: в первом случае, мы лишь случайным образом выполняем перетасовку в последовательности операций. В более рандомизированном варианте данного тестирования операции проходят не только перетасовку. Вместо этого, программа наугад выбирает общее число операций в группе из всех операций, имевших место в прошлом. Различие заключается в том, что при использовании последнего метода списки операций могут быть разными. Вы можете выбрать одну операцию несколько раз, а другие операции не выбирать вовсе.

2. Пропуская операции. Мы можем получить результат в отношении некоторых операций, которые случайным образом не будут использоваться (с заданной вероятностью). При осуществлении реальных торговых операций с имуществом часто можно потерять операцию в связи с платформой или интернетом, или просто потому, что в течение какого-то периода времени Вы не торговали. Данный тест даст Вам представление о том, какой будет кривая акций, если некоторые операции будут случайным образом пропущены.

Практическое использование метода Монте-Карло

Применение данного метода должно являться одним из последних шагов в разработке Вашей стратегии. Перед тем, как начать внедрение какой-либо стратегии, Вам необходимо выполнить моделирование Монте-Карло для реалистичной оценки ожиданий в отношении максимальной прибыли и убытков.

Уровень ожиданий и число моделирований. Лучше всего иметь уровень ожиданий, составляющий 95%, и выполнять, как минимум, 100 моделирований. Чем больше будет выполнено моделирований, тем будет выше статистическое значение. При этом лишь значение на уровне 95% будет указывать Вам на то, что вероятность получения худших результатов, чем результаты моделирования, равна 5%.

Максимальные убытки и чистая прибыль. Вам необходимо выполнить поиск значений, предложенных в ходе моделирования Монте-Карло, рассмотреть их как значения, которые могут иметь место в действительности, а также оценить свою готовность применить стратегию, предлагающую полученные ожидания в отношении прибыли и рисков.

Др. Марк Фрик

Др. Марк Фрик обладает научной степенью доктора наук в области программирования. Он является разработчиком программного обеспечения для торговых операций с опытом работы более 10 лет и главным архитектором программного обеспечения в StrategyQuant, компании по разработке программного обеспечения и технологий, посвященных продукции, связанной с алгоритмическими торговыми операциями и искусственным интеллектом.

tradersmag.ru

Метод Монте-Карло - часть 2

Тогда цены облигаций (на номинал в 100 долл.) через 6 месяцев определяются следующим образом:

P1 = 6/0,1 (1- 1/ (1+0,05)10)+100/(1+0,05)10 = 84,55653

P2 = 100 (купонная ставка совпадает с доходностью).

P3 = 10,5/0,09 (1 – 1/(1,045)50)+ 100/(1,045)50 = 114,82151

Значит, реализуемая доходность портфеля облигаций составит:

P1 * 5*104+P2*4*104+ P3* 6*104+15 *104+18*104+315*103-15*106=0,1016

15 * 106

Т.е. 10,16%

Предположим, что было проведено 100 итераций. При этом оказалось, что наименьшая реализуемая доходность портфеля равна -3,905%, а наибольшая реализуемая доходность составляет 24,97%.

Разделив отрезок (-3,905%; 24,97%) на достаточно большое число частей, подсчитаем для каждой части число итераций, дающих реализуемую доходность из этой части.

Таким образом, будет построено эмпирическое распределение вероятностей реализуемой доходности портфеля облигаций. После чего можно получить различные числовые характеристики этой реализуемой доходности: среднее значение, стандартное отклонение и т. д.

2. Метод Монте-Карло в условиях управления рыночными рисками.

Метод Монте-Карло, или метод стохастического моделирования (Monte Carlo simulation), основан на моделировании случайных процессов с заданными характеристиками. В отличие от метода исторического моделирования, в методе Монте-Карло изменения цен активов генерируются псевдослучайным образом в соответствии с заданными параметрами распределения, например математическим ожиданием μ и волатильностью σ. Имитируемое распределение может быть, в принципе, любым, а количество сценариев — весьма большим (до нескольких десятков тысяч). Выделяют:

метод Монте-Карло для одного фактора риска;

метод Монте-Карло для портфеля активов.

Рассмотрим Метод Монте-Карло для одного фактора риска. Моделирование траектории цен производится по различным моделям. Например, распространенная модель геометрического броуновского движения дает в итоге следующие выражения для моделирования цен S на каждом шаге процесса, состоящего из очень большого количества шагов, охватывающих период Т:

dSt = St (μdt + σdzt), (1)

, где dzt — винеровский случайный процесс.

Воспользовавшись определением винеровского процесса, уравнение (1) можно записать в дискретной форме:

σσ∆St= St-1 (μ∆t + σε√∆t) , (2)

т. е.

St+1 = St + St (μ∆t + σε1√∆t), (3)

St+1 = St+1 + St+1 (μ∆t + σε2√∆t), (4)

ST = St+n.

Если траектория цен состоит из n равных шагов (например, n дней), то один шаг ∆t = 1/n, а случайная величина ε подчиняется стандартному нормальному распределению (μ = 0, σ = 1). Можно использовать и иные модели эволюции цен, например экспоненциальную.

Траектория цен — это последовательность псевдослучайным образом смоделированных цен, начиная от текущей цены и заканчивая ценой на некотором конечном шаге, например на тысячном или десятитысячном. Чем больше число шагов, тем выше точность метода.

Каждая траектория представляет собой сценарий, по которому определяется цена на последнем шаге исходя из текущей цены. Затем производится полная переоценка портфеля по цене последнего шага и расчет изменения его стоимости для каждого сценария. Оценка VaR производится по распределению изменений стоимости портфеля.

Генерация случайных чисел в методе Монте-Карло состоит из двух шагов. Сначала можно воспользоваться генератором случайных чисел, равномерно распределенных на интервале между 0 и 1 (рассмотрено выше). Затем, используя как аргументы полученные случайные числа, вычисляют значения функций моделируемых распределений.

Однако следует помнить, что генераторы случайных чисел работают на детерминированных алгоритмах и воспроизводят так называемые «псевдослучайные числа», поскольку с некоторого момента последовательности этих псевдослучайных чисел начинают повторяться, т. е. они не являются независимыми. В простейших генераторах это происходит уже через несколько тысяч генераций, а в более сложных— через миллиарды генераций. Если массив случайных чисел начинает повторяться слишком быстро, то метод Монте-Карло перестает моделировать случайные, независимые сценарии и оценка VaR начинает отражать ограниченность генератора, а не свойства портфеля. Оптимальное количество шагов в процессе зависит от объема выборки, состава портфеля и сложности составляющих его инструментов и др.

Рассмотрим пример: элементы расчета VaR методом Монте-Карло на современном российском рынке. Для расчета VaR можно использовать различные модификации метода Монте-Карло; в данном случае метод описывается следующим образом:

По ретроспективным данным рассчитываются оценки математического ожидания х и волатильности σ.

С помощью датчика случайных чисел генерируются нормально распределенные случайные числа ε с математическим ожиданием, равным х, и стандартным отклонением σ.

Полученными на предыдущем шаге случайными числами ε заполняется таблица размерностью 500 столбцов на 1000 строк (вообще говоря, размерность таблицы произвольная и зависит, например, от имеющихся вычислительных мощностей, но, чтобы метод обеспечивал приемлемую точность, она должна быть достаточно большой).

Вычисляется траектория моделируемых цен вплоть до S1000 по формуле St= St-1e εt-1, где е — основание натурального логарифма, St— текущая цена (курс) актива.

Производится переоценка стоимости портфеля (состоящего в данном примере из одного актива) по формуле: ∆V= Q (S1000 – S0), где Q — количество единиц актива.

Шаги 4 и 5 выполняются 500 раз для заполнения таблицы 500 х 1000. Полученные 500 значений ∆V сортируются по убыванию (от самого большого прироста до самого большого убытка). Эти ранжированные изменения можно пронумеровать от 1 до 500. В соответствии с желаемым уровнем доверия (1 - α) риск-менеджер может определить VaR как такой максимальный убыток, который не превышается в 500(1 - α) случаях, т. е. VaR равен абсолютной величине изменения с номером, равным 500(1 - α).

Шаги 1-6 повторяются для каждого расчета каждого дневного VaR.

В качестве объекта исследования был выбран индекс РТС. Генерация случайных чисел производилась при помощи встроенного генератора МS Ехсеl.

Метод Монте-Карло является наиболее технически сложным из всех описанных методов расчета VaR. Кроме того, для выполнения расчетов в полном объеме необходимы значительные вычислительные мощности и временные ресурсы. Современные компьютеры пока еще не позволяют обрабатывать информацию в режиме реального времени, как этого требуют трейдеры, если риск-менеджеры хотят устанавливать VaR-лимиты на величину открытых позиций с помощью метода Монте-Карло.

Существует вариант метода Монте-Карло, согласно которому можно не задавать какое-либо конкретное распределение для моделирования цен, а использовать непосредственно исторические данные. Подобно методу исторического моделирования, на основе ретроспективы моделируются гипотетические цены, но их последовательность не является единственной и не ограничена глубиной периода ретроспективы, поскольку выборка производится с возвращением (bootstrap), т. е. возмущение из исторических данных выбирается случайным образом, и каждый раз в выборе участвуют все данные. Такое построение выборки исторических данных позволяет учесть эффект «толстых хвостов» и скачки цен, не строя предположений о виде распределения. Это несомненные достоинства метода, который, в отличие от метода исторического моделирования, позволяет рассмотреть не какую-либо одну траекторию цен (сценарий), а сколь угодно много, что, как правило, повышает точность оценок. Недостатками данной методики являются низкая точность при малых объемах выборки и использование предположения о независимости доходностей во времени.

Теперь рассмотрим метод Монте-Карло для портфеля активов. Чтобы проводить моделирование по Монте-Карло для многофакторного процесса, можно точно так же моделировать каждый из к рассматриваемых факторов исходя из сгенерированных случайных чисел:

dSt,j = μt,j St,j dt + σt,j St,j Sdzt,j, j = 1,2, …, k, (5)

или для дискретного времени:

∆St,j = St-1,j(μj∆t + σjεj√∆t), j = 1,2, …, k. (6)

С целью учета корреляции между факторами необходимо, чтобы случайные величины εi и εj точно так же коррелировали между собой. Для этого используется разложение Холецкого, суть которого состоит в разложении корреляционной матрицы на две (множители Холецкого) и использовании их для вычисления коррелированных случайных чисел.

Корреляционная матрица является симметричной и может быть представлена произведением треугольной матрицы низшего порядка с нулями в верхнем правом углу на такую же транспонированную матрицу. Например, для случая двух факторов имеем:

Отсюда

Коррелированные случайные числа ε1 и ε2 получаются путем перемножения множителя Холецкого и вектора независимых случайных чисел η:

mirznanii.com

Сущность метода Монте-Карло и моделирование случайных величин

Введение

Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.

Датой рождение метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «Метод Монте-Карло» (Н. Метрополис, С. Улам). Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В нашей стране первые статьи были опубликованы в 1955–56 гг. (В.В. Чавчанидзе, Ю.А. Шрейдер, В.С. Владимиров)

Однако теоретическая основа метода была известна давно. Кроме того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т.е. фактически методом Монте-Карло. Однако до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, так как моделировать случайные величины вручную – очень трудоёмкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ.

Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом, а одним из простейших механических приборов для получения случайных величин является рулетка.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий круг задач статистической физики, очень разных по своему содержанию. К разделам науки, где всё в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.

Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественность получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.

В подавляющем большинстве задач, решаемых методами Монте-Карло, вычисляют математические ожидания некоторых случайных величин. Так как чаще всего математические ожидания представляют собой обычные интегралы, в том числе и кратные, то центральное положение в теории методов Монте-Карло занимают методы вычисления интегралов.

1. Теоретическая часть

1.1 Сущность метода Монте-Карло и моделирование случайных величин

Предположим, что нам необходимо вычислить площадь плоской фигуры

. Это может быть произвольная фигура, заданная графически или аналитически (связная или состоящая из нескольких частей). Пусть это будет фигура, заданная на рис. 1.1.

Рис. 1.1

Предположим, что эта фигура расположена внутри единичного квадрата.

Выберем внутри квадрата

случайных точек. Обозначим через

число точек, попавших внутрь фигуры

. Геометрически видно, что площадь фигуры

приближенно равна отношению

. Причем, чем больше число

, тем больше точность этой оценки.

Для того чтобы выбирать точки случайно, необходимо перейти к понятию случайная величина. Случайная величина

непрерывная, если она может принимать любое значение из некоторого интервала

Непрерывная случайная величина

определяется заданием интервала

, содержащего возможные значения этой величины, и функции

, которая называется плотностью вероятностей случайной величины

(плотностью распределения

). Физический смысл

следующий: пусть

- произвольный интервал, такой что

, тогда вероятность того, что

окажется в интервале

, равна интегралу

(1.1)

Множество значений

может быть любым интервалом (возможен случай

). Однако плотность

должна удовлетворять двум условиям:

1) плотность

положительна:

; (1.2)

2) интеграл от плотности

по всему интервалу

равен 1:

(1.3)

Математическим ожиданием непрерывной случайной величины называется число

(1.4)

Дисперсией непрерывной случайной величины называется число:

Нормальной случайной величиной называется случайная величина

, определённая на всей оси

и имеющая плотность

(1.5)

где

- числовые параметры

Любые вероятности вида

легко вычисляются с помощью таблицы, в которой приведены значения функции

, называемой обычно интегралом вероятностей.

Согласно (1.1)

В интеграле сделаем замену переменной

, тогда получим

где

Отсюда следует, что

Также

Нормальные случайные величины очень часто встречаются при исследовании самых различных по своей природе вопросов.

Выбрав

, найдём

. Следовательно,

(1.6)

Вероятность

настолько близка к 1, что иногда последнюю формулу интерпретируют так: при одном испытании практически невозможно получить значение

, отличающееся от

больше чем на

Проводя большое количество опытов, и получая большое количество случайных величин можно воспользоваться центральной предельной теоремой теории вероятностей. Эта теорема впервые была сформулирована П. Лапласом. Обобщением этой теоремы занимались многие выдающиеся математики, в том числе П.Л. Чебышёв, А.А. Марков, А.М. Ляпунов. Её доказательство достаточно сложно.

Рассмотрим

одинаковых независимых случайных величин

, так что распределения вероятностей этих величин совпадают. Следовательно, их математические ожидания и дисперсии также совпадают. Величины эти могут быть как непрерывными, так и дискретными.

Обозначим

mirznanii.com

Анализ результатов торговли методом Монте-Карло и опасность недокапитализации. Метод монте карло биржа

Практикум для трейдера. Системный трейдинг

Анализ результатов торговли методом Монте-Карло и опасность недокапитализации

Метод Монте Карло в трейдинге - 2018-03-01

Метод Монте Карло: описание

Как же работает Монте Карло алгоритм?

Метод Монте Карло: пример

Расчет премии по опциону методом Монте-Карло vs формула Блэка-Шоулза / Хабр

Программное моделирование покупки опциона

Устранение тренда

Построение и использование обратной кумулятивной функции распределения

Результаты моделирования

Расчет премии по рыночным контрактам

Рекомендации к практической оценке премии опционного контракта

Насколько надежна Ваша стратегия? Введение в метод Монте-Карло.

Метод Монте-Карло - часть 2

Сущность метода Монте-Карло и моделирование случайных величин

Смотрите также