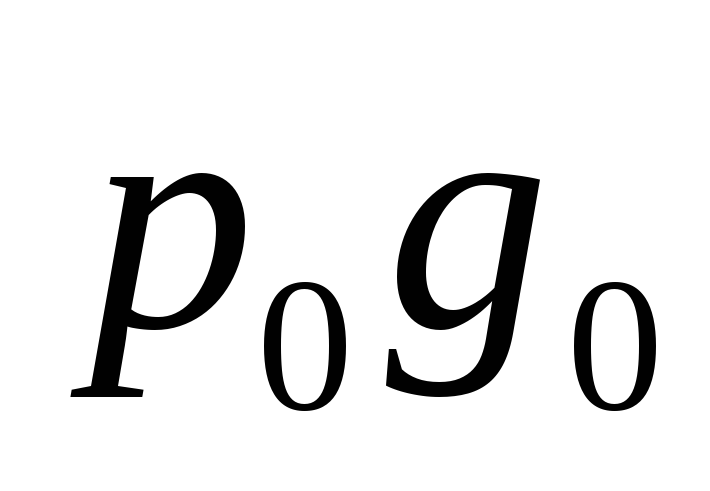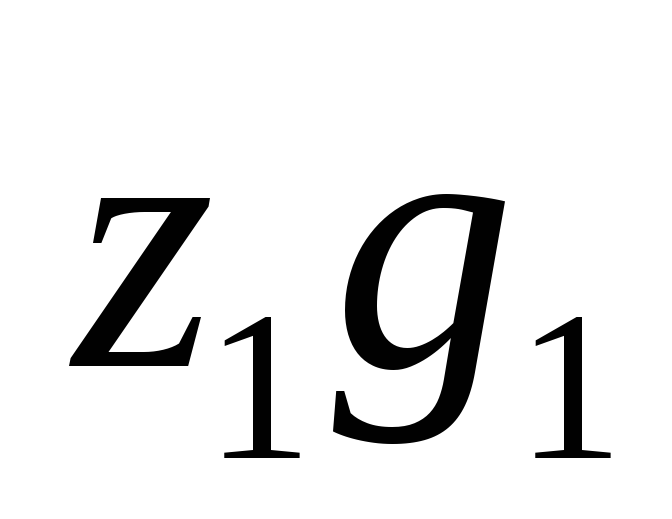2.4. Задачи для самостоятельной работы. Продажа грузовых автомобилей на товарной бирже города характеризуется следующими данными
Решение типовых задач
Пример 1
Итоги торгов Сибирской межбанковской валютной биржи (СМВБ) характеризовались следующими данными, 2013 год:
| Валюта | Курс, руб. | Продано, млн. шт. | ||
| 7.07 | 14.07 | 7.07. | 14.07 | |
| Р0 | Р1 | g0 | g1 | |
| $ USA | 29,82 | 30,06 | 15,11 | 14,07 |
| EUR | 34,33 | 34,65 | 13,52 | 16,30 |
Рассчитайте:
индивидуальные и общие индексы курсов валют, физического объема продаж и оборота СМВБ за неделю;
абсолютное изменение оборота всего и в том числе за счет изменения курсов валют и физического объема продаж;
покажите взаимосвязь между исчисленными индексами.
Решение
1. Индивидуальные индексы равны:
а) курсов валют 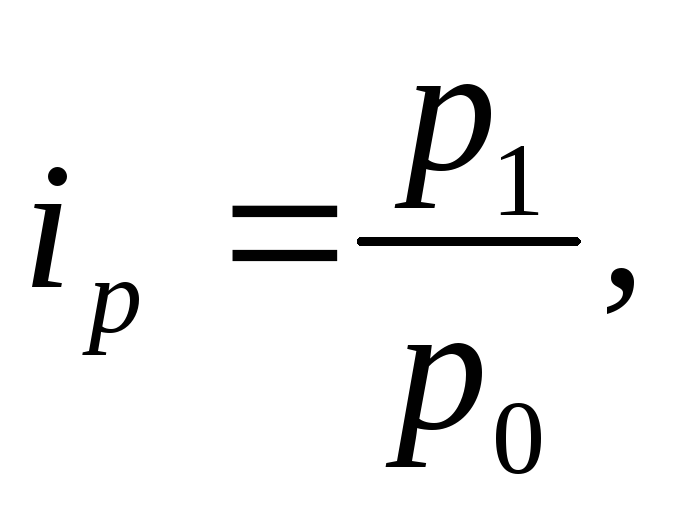
где 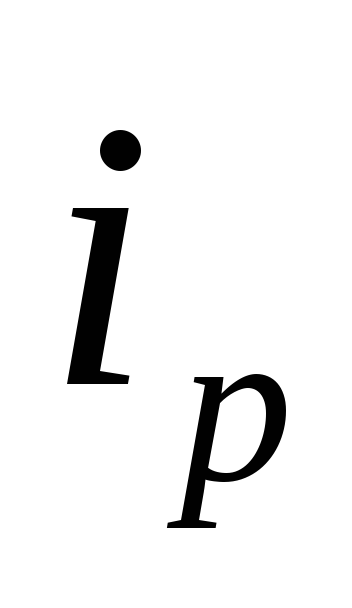 - индивидуальный индекс цены;
- индивидуальный индекс цены;
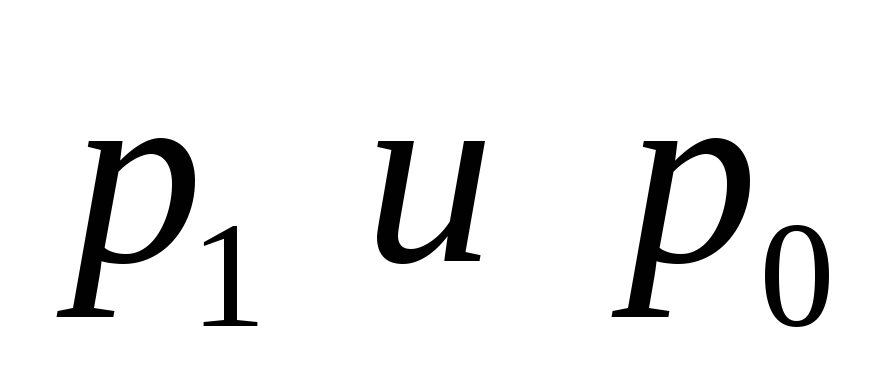 - цена отчетного и базисного периодов;
- цена отчетного и базисного периодов;
б) физического объема проданных валют 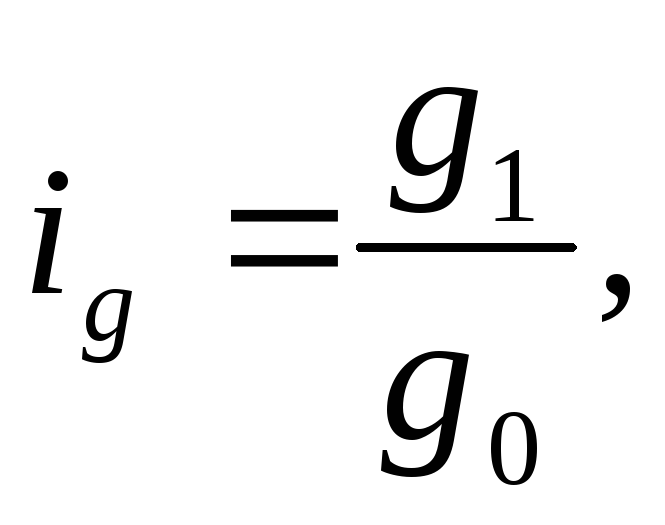
где 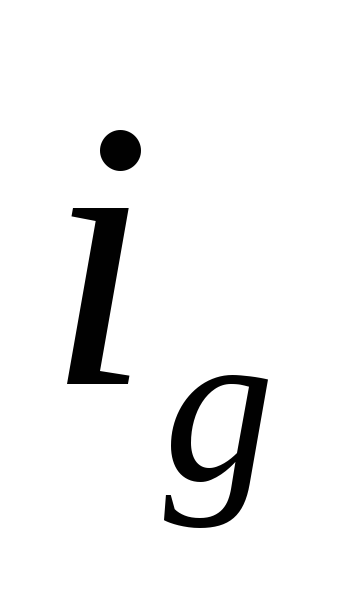 - индивидуальный индекс физического объема;
- индивидуальный индекс физического объема;
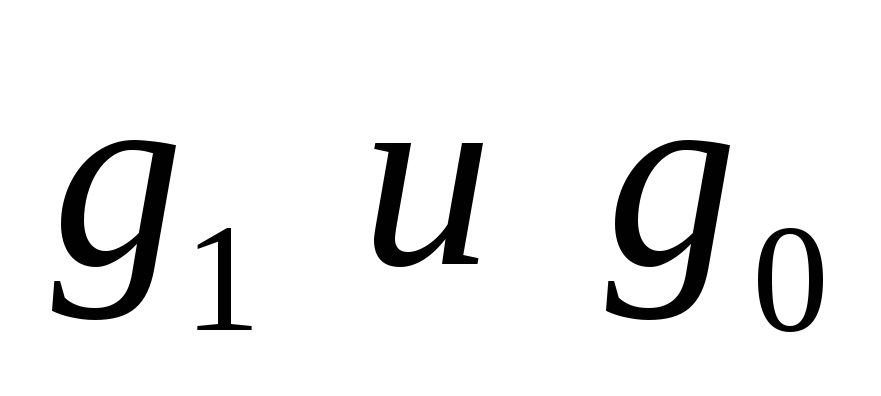 - объем проданных валют отчетного и базисного периодов;
- объем проданных валют отчетного и базисного периодов;
Так, для $ USA 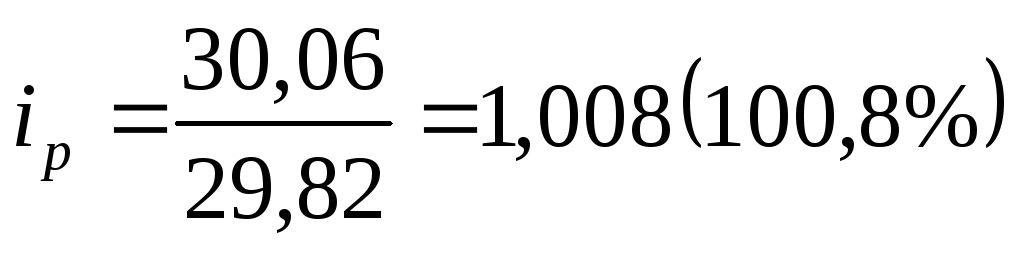 ;
;

Следовательно, курс доллара США увеличился на 0,8%, а объем проданных долларов США сократился на 6,9%.
Соответствующие индексы для EUR будут равны

Таким образом, при незначительном росте курса EUR, существенно возрос объем продаж.
2. Общий индекс оборота торгов 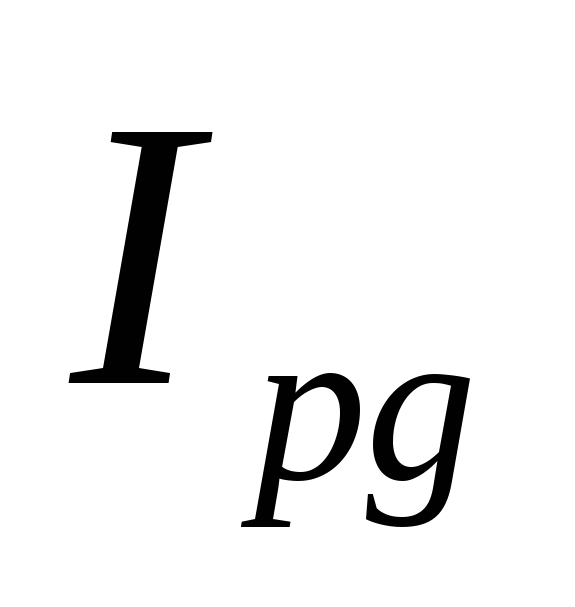 исчисляется по формуле:
исчисляется по формуле:
 ,
,
где 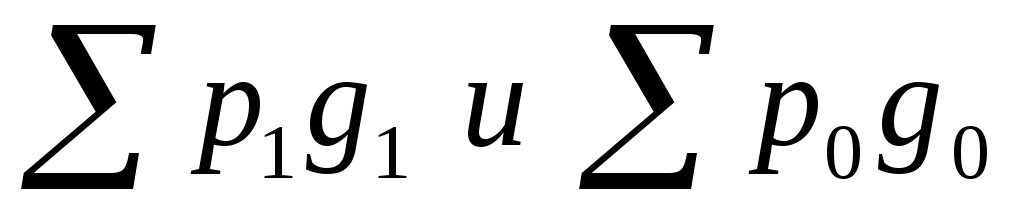 - оборот торгов за отчетный и базисный периоды.
- оборот торгов за отчетный и базисный периоды.
Это означает, что оборот СМВБ за неделю возрос на 8%.
3. Общий индекс физического объема валют 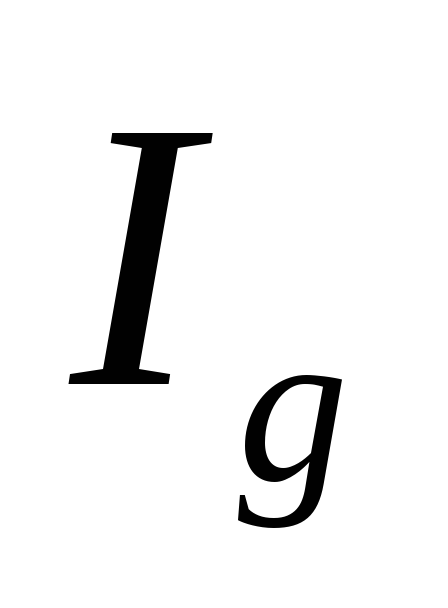 определим по формуле:
определим по формуле:

где 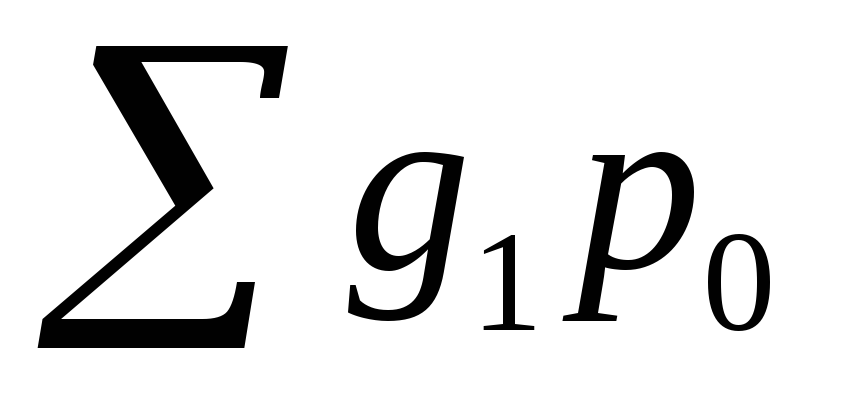 - условный объем торгов отчетного периода в ценах базисного.
- условный объем торгов отчетного периода в ценах базисного.
Из чего можно заключить, что, несмотря на значительный рост объема продаж EUR общий объем проданных валют в среднем увеличился на 7,0%.
4. Общий индекс курса валют 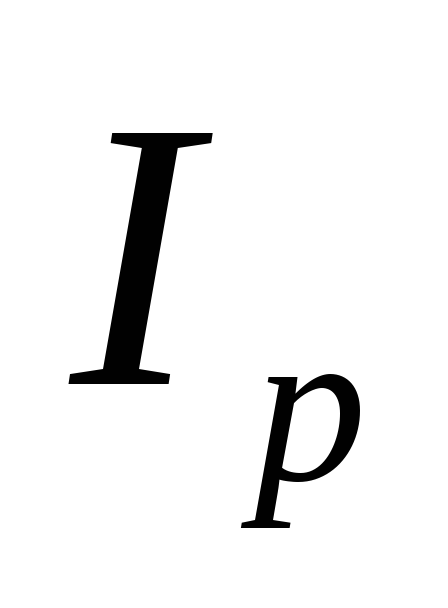 равен:
равен:
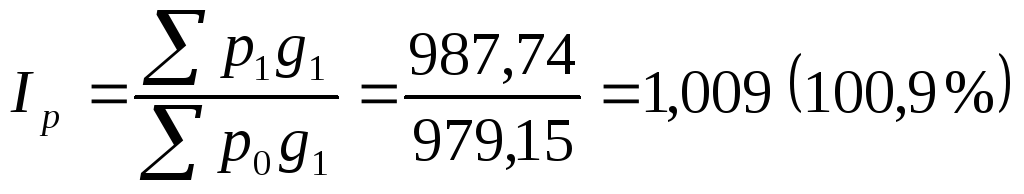 ,
,
то есть курс обеих валют в среднем вырос на 0,9%.
5. Прирост или снижение оборота торгов исчисляется как разница между числителем и знаменателем индекса оборота торгов: 

Общий абсолютный прирост обусловлен изменением курсов валют и изменением количества проданных валют.
Прирост за счет изменения курсов валют составит:
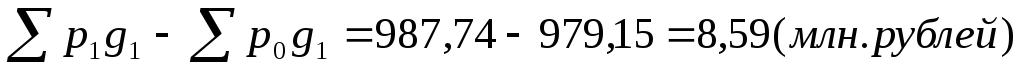
Прирост за счет изменения физического объема продаж равен:
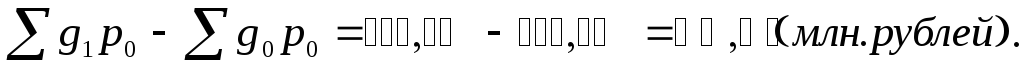
На основании проведенного анализа следует, что общий абсолютный прирост, равный 73,02 млн. рублей получен за счет роста курса валют на 8,59 млн. рублей и за счет увеличения объема продаж на 64,43 млн. рублей.
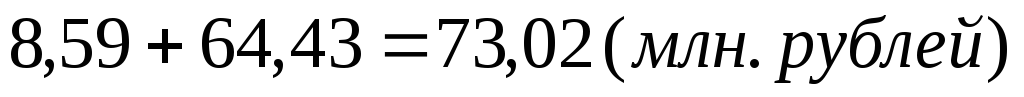
6. Между исчисленными индексами существует взаимосвязь:
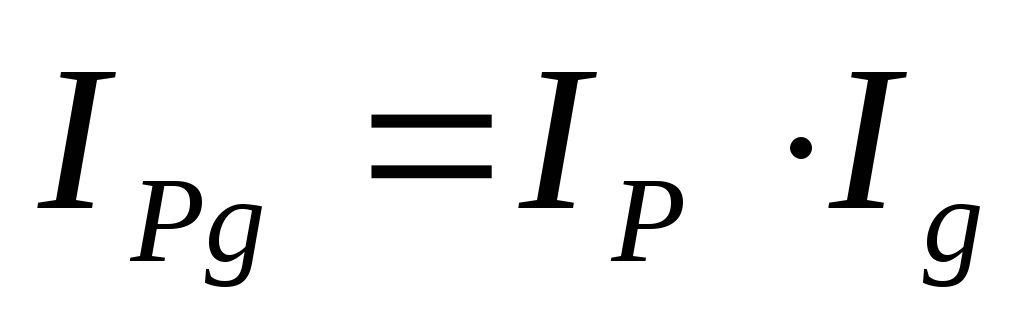
что и нашло свое подтверждение
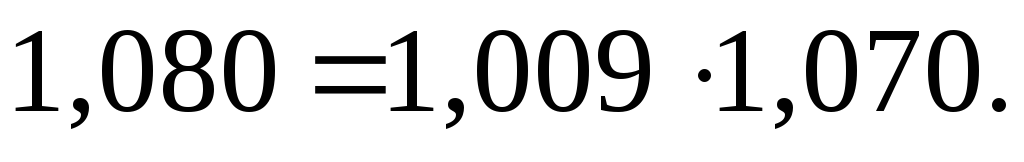
Проанализировать происходящие изменения торгов СМВБ (на примере одной из валют) возможно и при помощи графического метода.
Наглядно это можно показать с помощью особого вида плоскостной диаграммы, известной в статистике как «знак Варзара» (по имени русского статистика В.Е. Варзара (1851-1940)). В качестве примера воспользуемся ситуацией с EUR (рисунок 1)
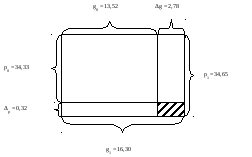
Рисунок 1 - Графическое изображение влияние изменения курса EUR (рублей) (р) и объема продаж (млн. шт.) (g) на объем торгов (млн. рублей) (рg).
Результативное явление представлено в виде прямоугольника, площадь которого в базисном периоде  , в отчетном
, в отчетном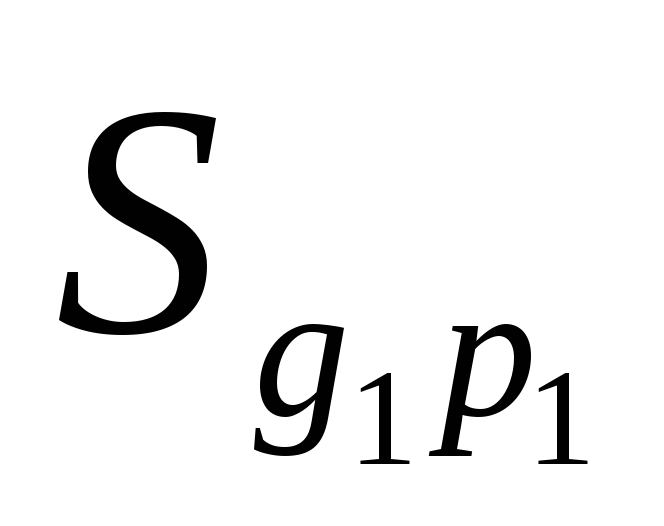 .
.
Переход от базисного состояния к отчетному формируется за счет изменения факторов g (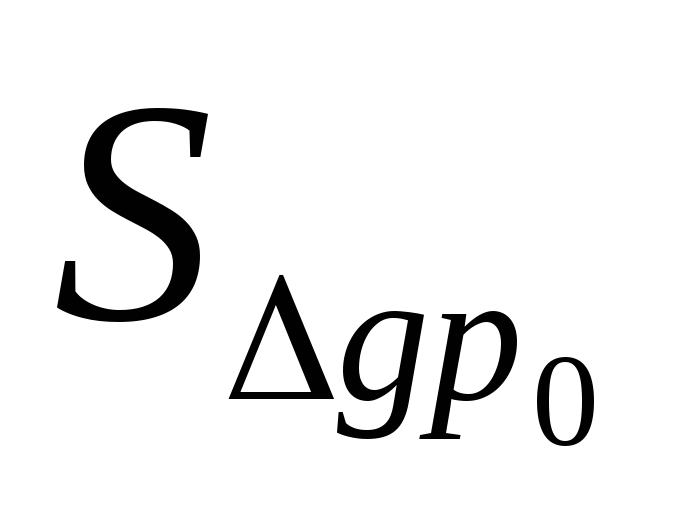 ), изменения факторар (
), изменения факторар (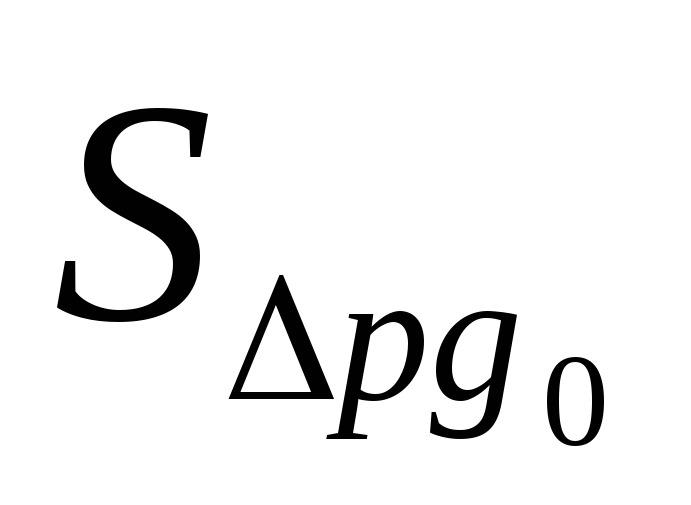 ) и совместного изменения двух факторовp и g (
) и совместного изменения двух факторовp и g (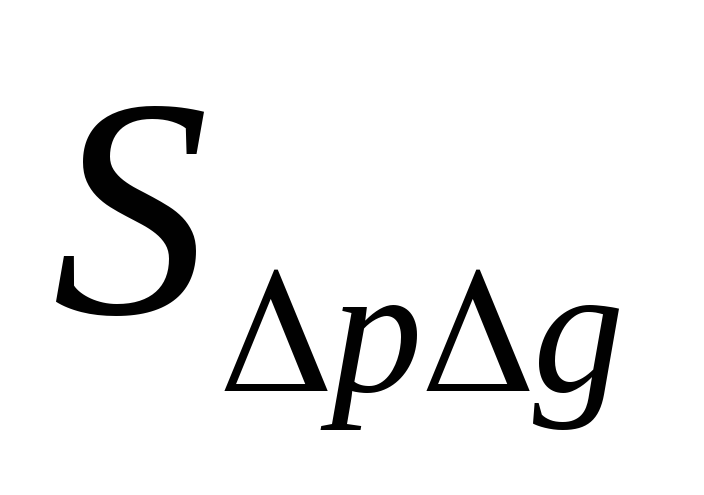 ):
):
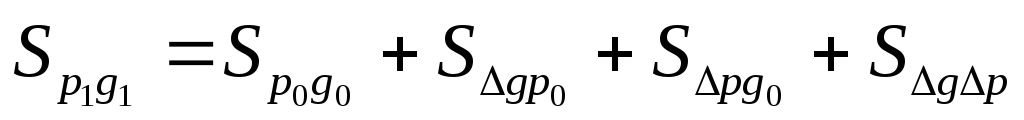
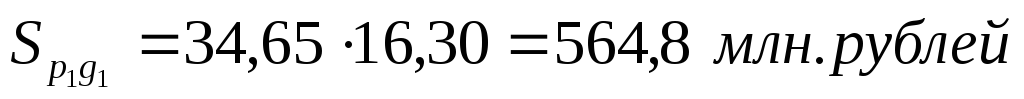
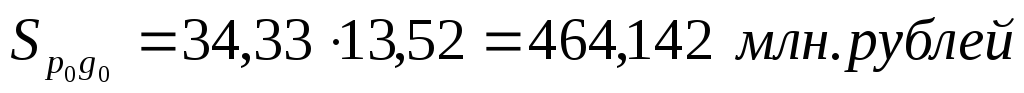
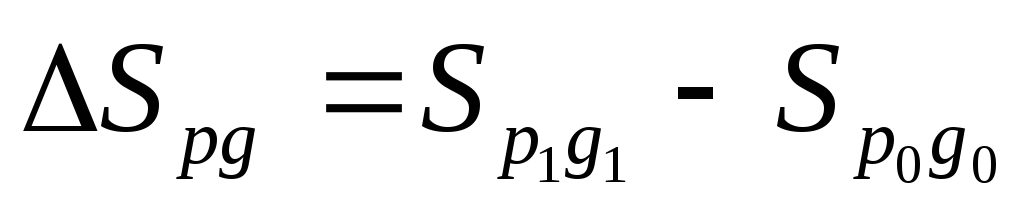
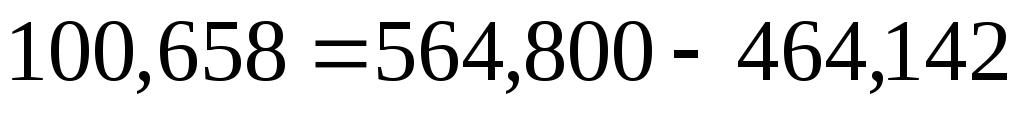
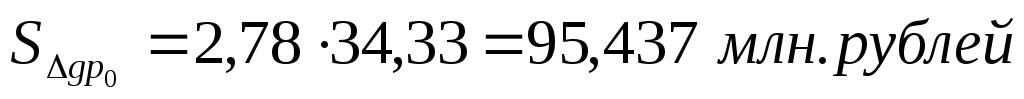
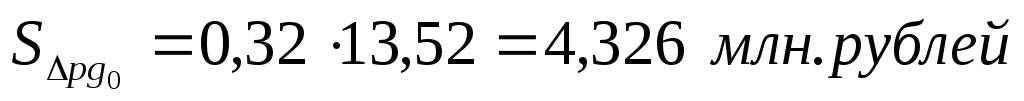
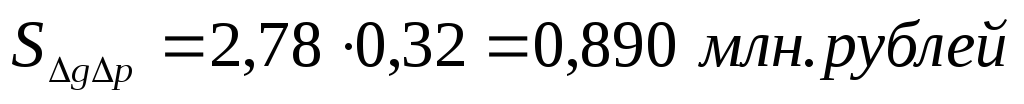
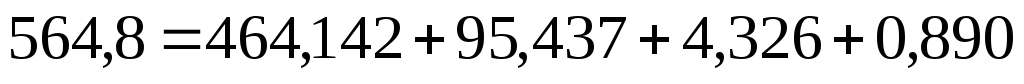
Таким образом, оборот торгов СМВБ по EUR на 14.07 составил 564,800 млн. рублей. Абсолютный прирост за анализируемую неделю равен 100,658 млн. рублей. Это величина получена за счет скачка объема продаж (95,437 млн. рублей), за счет роста курса EUR (4,326 млн. рублей) и за счет их совместного влияния (0,890 млн. рублей).
7. Анализ влияния курса валюты как интенсивного фактора и физического объема как экстенсивного фактора на изменение оборота продаж в упрощенном виде производится по следующей методике:
(рассмотрим на примере $ USA).
Общее изменение оборота 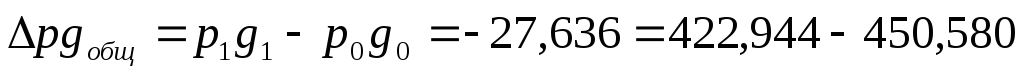
Изменение оборота СМВБ под влиянием изменения курса валюты:
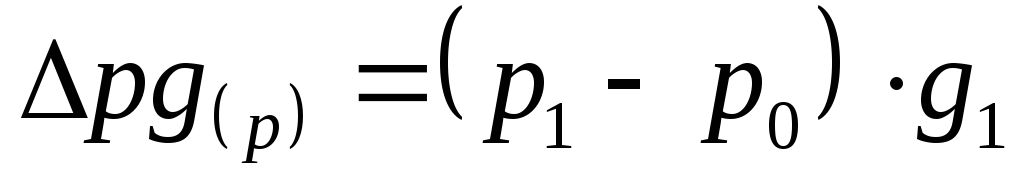
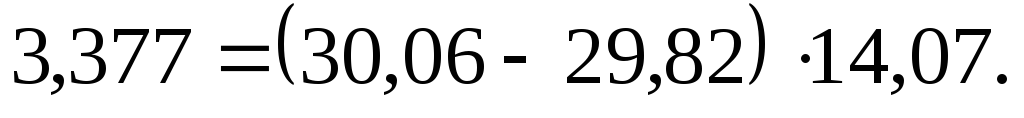
.
Изменение оборота продаж биржи под влиянием изменения физического объема долларов США:
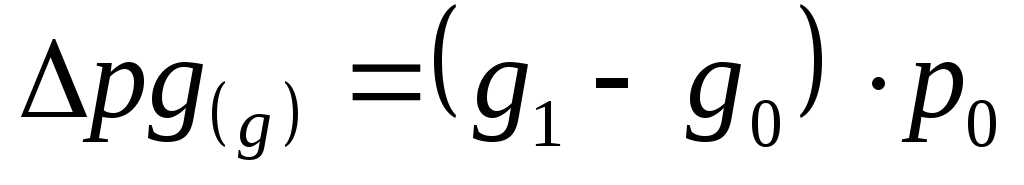
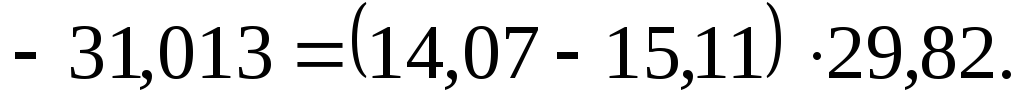
В итоге 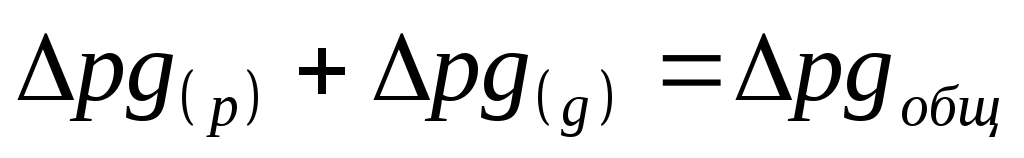
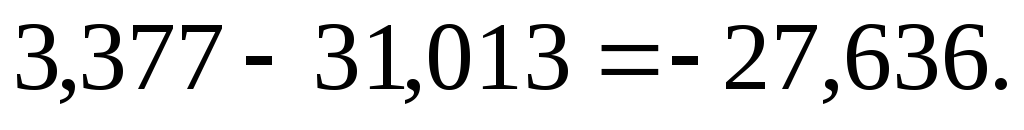
Полученные результаты свидетельствуют о том, что объем торгов $ за период с 7.07 по 14.07 сократился на 27,636 млн. рублей. В основном на полученный результат оказало влияние сокращение физического объема продаж долларов США (31,013 млн. рублей) и незначительное повышение курса валюты (3,377 млн. рублей).
Проведенные расчеты позволили более детально изучить происходящие процессы на СМВБ за данный период. На основании анализа можно констатировать, что с 7.07 по 14.07 физический объем продаж доллара США сократился на 6,9% (31,013 млн. рублей), незначительно возрос курс валюты 0,8%, что составляет 3,377 млн. рублей. В то же время скачок физического объема продаж EUR на 20,6% позволил дополнительно получить 95,437 млн. рублей. Рост курса EUR также незначителен 0,9% (4,326 млн. рублей). Происходящие процессы повлекли за собой прирост оборота торгов на 73,02 млн. рублей (8,0%), причем это достигнуто за счет увеличения объема торгов EUR на 100,658 млн. рублей и снижения объема торгов доллара США на 27,636 млн. рублей. Общий физический объем продаж валют в среднем увеличился на 7,0% или 64,43 млн. рублей, а курс валют EUR и доллара США в среднем вырос на 0,9% или 8,59 млн. рублей.
Пример 2
Имеются данные о выпуске кирпича по двум домостроительным комбинатам города:
| Домостро- ительный комбинат | Базисный период | Отчетный период | ||||
| Произведено продукции, тыс. шт. | Себестоимость продукции, руб. | Удельный вес продукции комбината | Произведено продукции, тыс. шт. | Себестоимость продукции, руб. | Удельный вес продукции комбината | |
| g0 | z0 | d0 | g1 | z1 | d1 | |
| ДСК-1 | 90 | 36 | 0,53 | 140 | 32 | 0,40 |
| ДСК-2 | 80 | 30 | 0,47 | 210 | 35 | 0,60 |
| Итого | 170 | 1,00 | 350 | 1,00 | ||
Определите:
индивидуальные индексы себестоимости производства кирпича;
общий индекс затрат на все изделия;
общий индекс себестоимости единицы изделия;
общий индекс физического объема продукции;
Рассчитайте индексы себестоимости продукции:
переменного состава;
фиксированного состава;
влияние структурных сдвигов.
Сделайте выводы и покажите взаимосвязь индексов.
Решение
1. Индивидуальные индексы себестоимости продукции 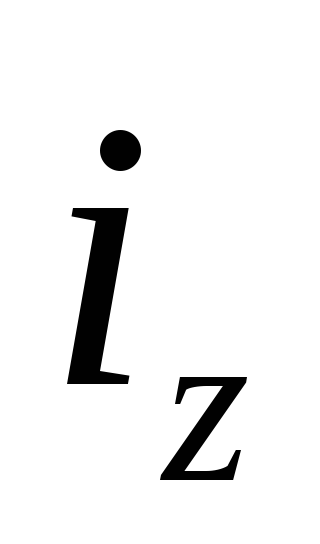 определим как:
определим как: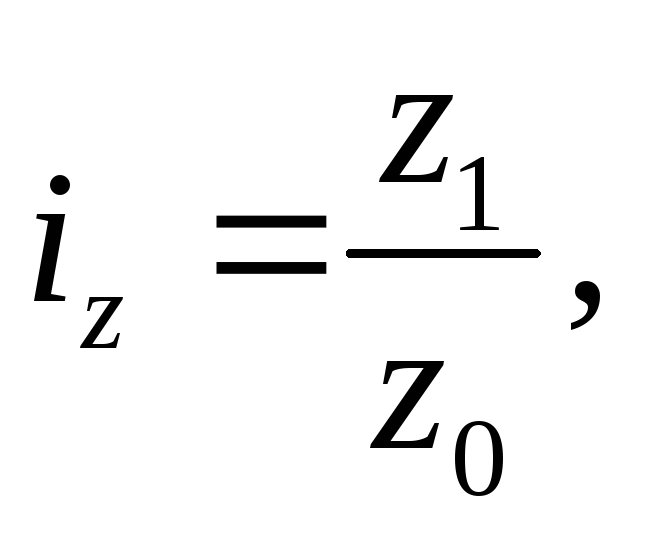
где 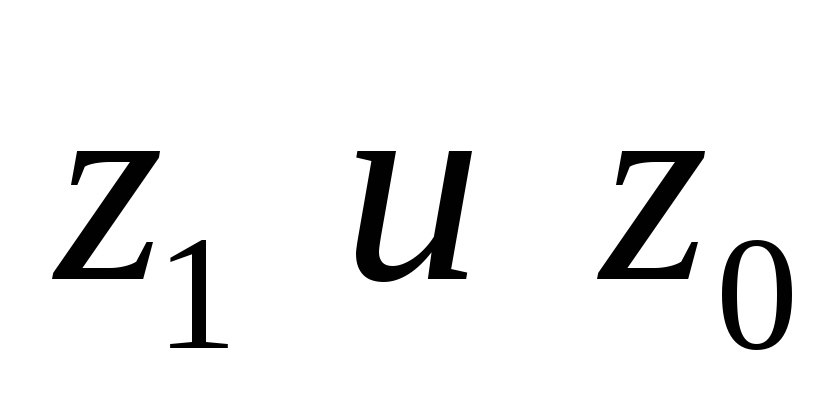 - себестоимость продукции отчетного и базисного периодов,
- себестоимость продукции отчетного и базисного периодов,
а) по ДСК-1 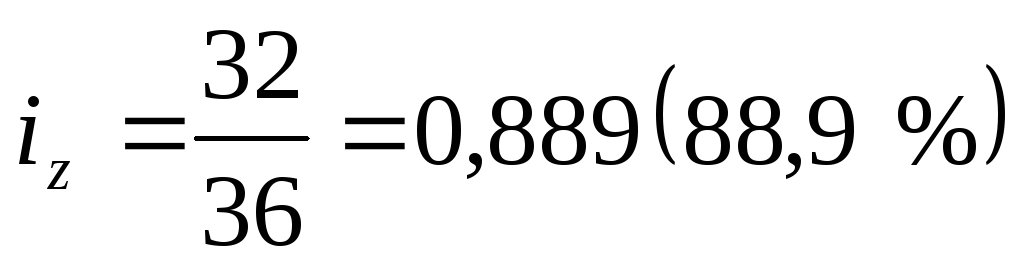
б) по ДСК-2 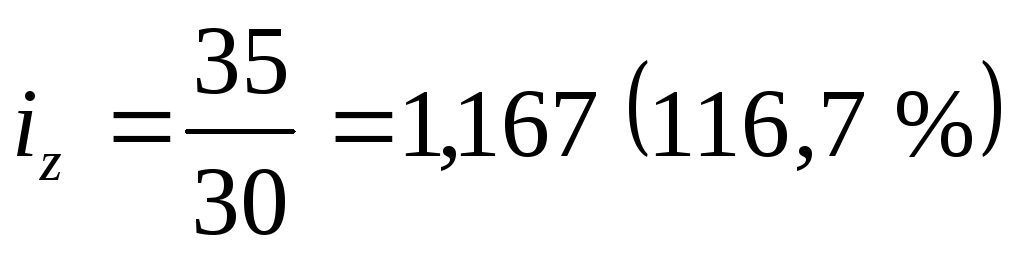
Положительные тенденции снижения себестоимости производства наблюдаются на ДСК-1 (11,1 %), в то время как себестоимость кирпича на втором комбинате возросла на 16,7 %.
2. В целом, для определения общего изменения уровня себестоимости продукции, выпускаемой домостроительными комбинатами, рассчитаем сводный индекс себестоимости производства( ):
):
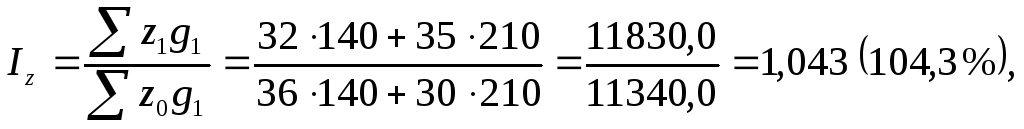
где 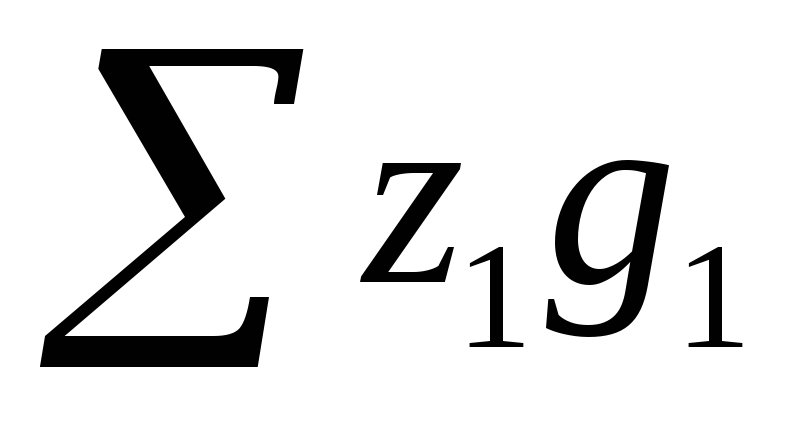 - общие затраты на производство отчетного периода;
- общие затраты на производство отчетного периода;
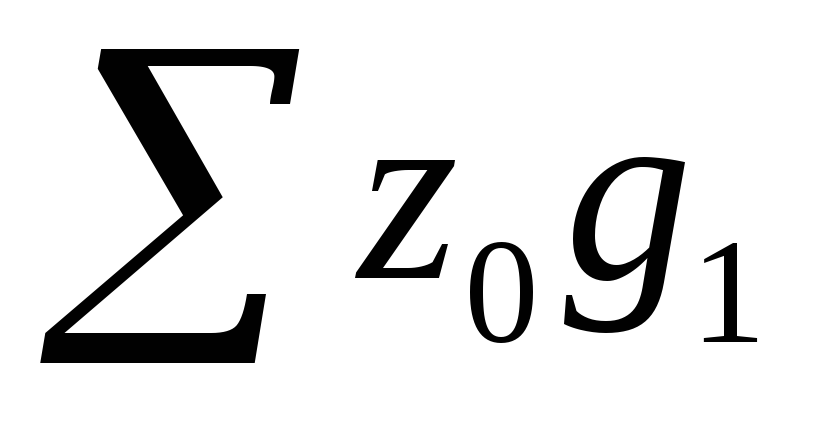 - условные затраты при себестоимости базисного периода.
- условные затраты при себестоимости базисного периода.
Мы получили, что себестоимость возросла в среднем на 4,3 %.
Разность числителя и знаменателя показывает сумму перерасхода предприятий от роста себестоимости производства на 4,3 %:
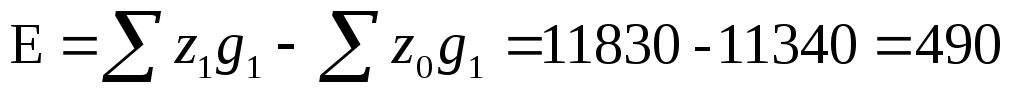 тыс. руб.
тыс. руб.
3. Сводный индекс физического объема продукции (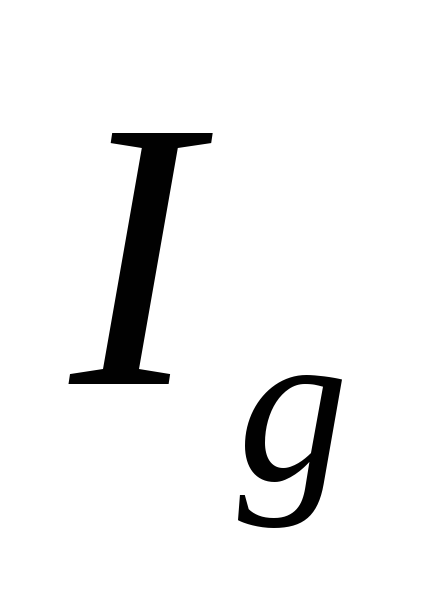 ), имеет следующий вид:
), имеет следующий вид:
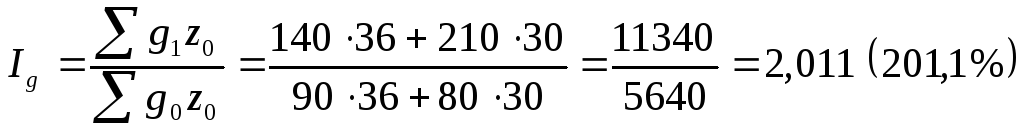 ,
,
где 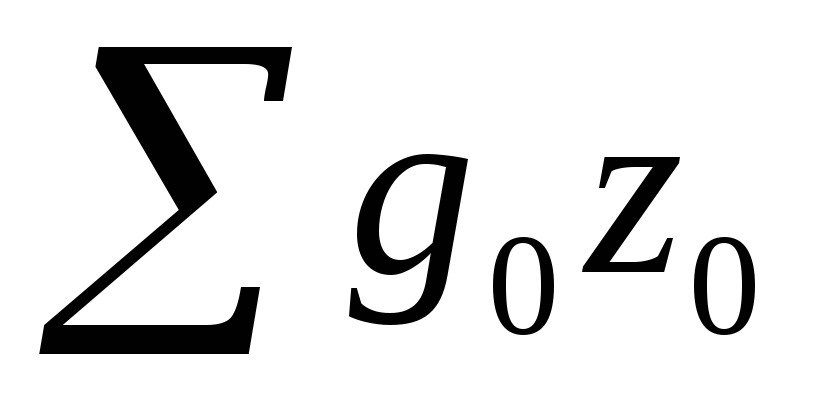 - общие затраты на производство базисного периода;
- общие затраты на производство базисного периода;
Следовательно, объем выпуска продукции на ДСК города возрос более чем в 2 раза.
4.Определив, составляющие общих затрат на производство вычислим сводный индекс затрат (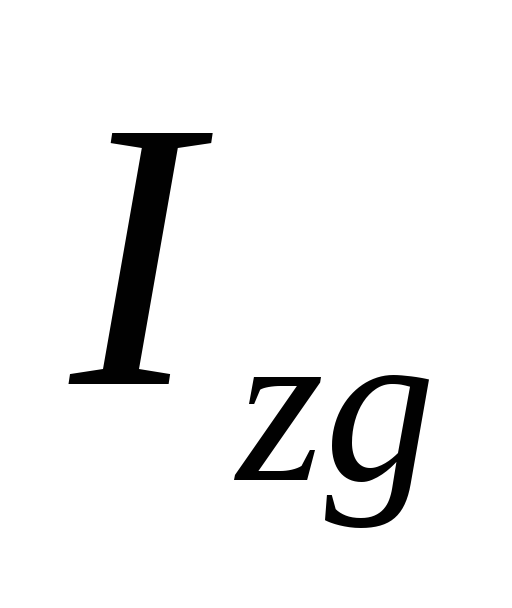 ):
):
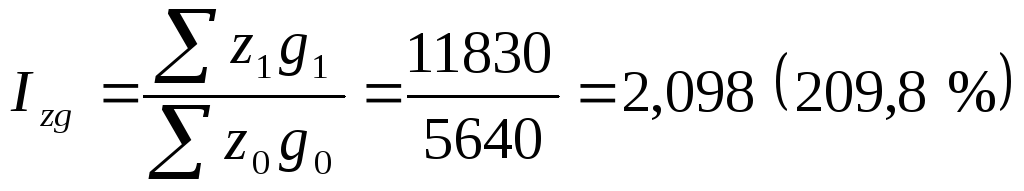
Таким образом, подученный результат еще раз подтверждает, что рост себестоимости (104,3 %) и объема производства (201 %) повлекли увеличение затрат более чем в 2 раза, т.е. на 109,8 %.
В абсолютном размере 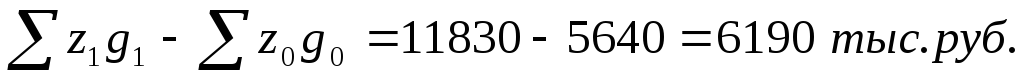
5. Проверим правильность проведенных вычислений, воспользовавшись взаимосвязью индексов.
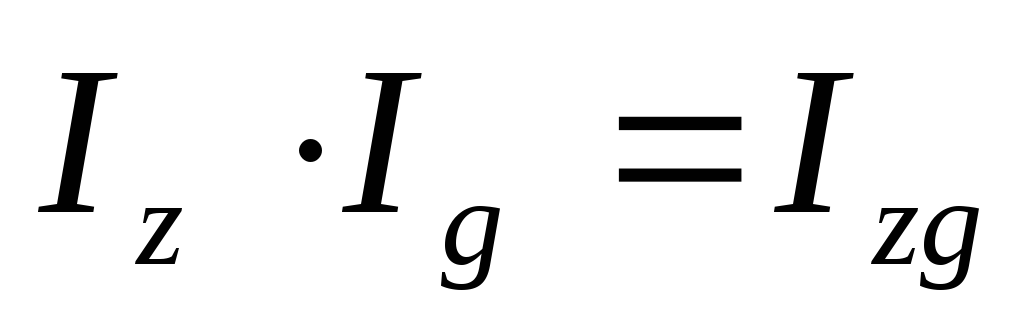
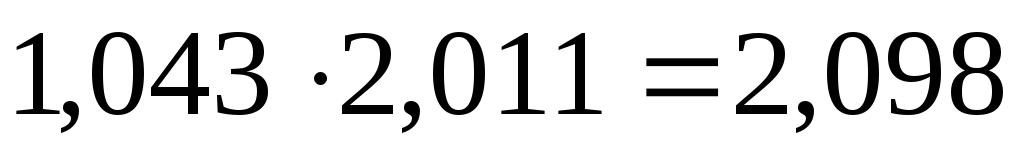
6. Определим индекс себестоимости переменного состава, который равен соотношению средней себестоимости продукции по двум комбинатам:
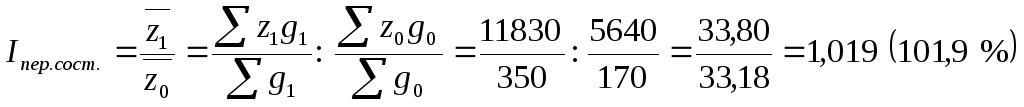
Индекс показывает, что средняя себестоимость кирпича по двум ДСК увеличилась на 1,9 %. Это увеличение обусловлено изменением себестоимости продукции по каждому комбинату и изменением структуры (удельного веса продукции комбинатов).
7. Выявим влияние каждого из этих факторов на динамику средней себестоимости, исчислив индексы себестоимости фиксированного состава и влияния структурных сдвигов.
а) индекс себестоимости фиксированного состава:
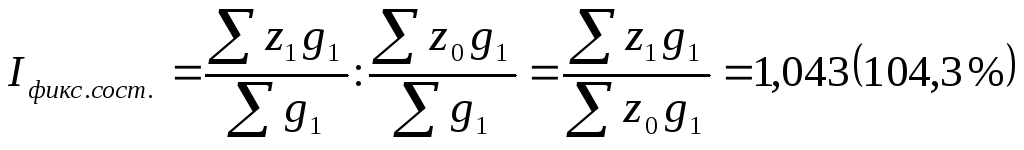
Себестоимость продукции в среднем возросла на 4,3 %.
б) индекс влияния структурных сдвигов.
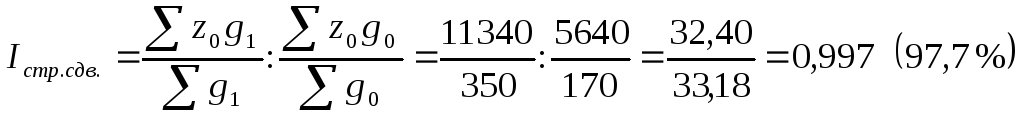
Средняя себестоимость изделия в отчетном периоде снизилась дополнительно на 2,3 % за счет изменения структуры, т.е. за счет роста удельного веса продукции ДСК-2 с 55 % до 60 % (здесь уровень себестоимости продукции был ниже по сравнению с ДСК-1).
8. Исчисленные индексы можно определить по удельным весам продукции комбинатов, выраженным в коэффициентах:
а) 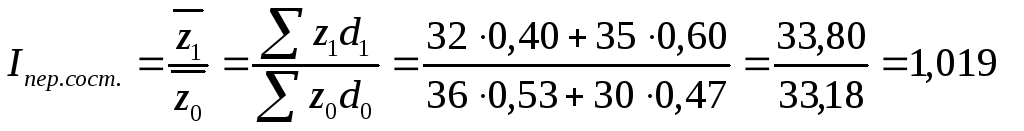 ,
,
где  - удельные веса продукции в отчетном и базисном периодах;
- удельные веса продукции в отчетном и базисном периодах;
Таким образом, в целом по комбинатам себестоимость кирпича возросла на 1,9 %. Абсолютное изменение (рост) себестоимости производства равен:
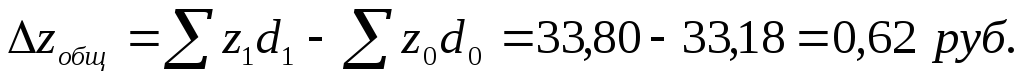
б) 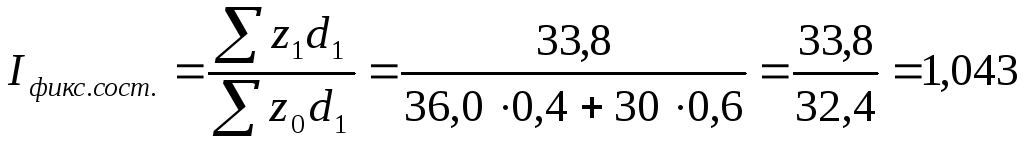
Следовательно, за счет изменения себестоимости продукции по каждому ДСК себестоимость в среднем по комбинатам возросла на 4,3 %, что в абсолютном размере составило:
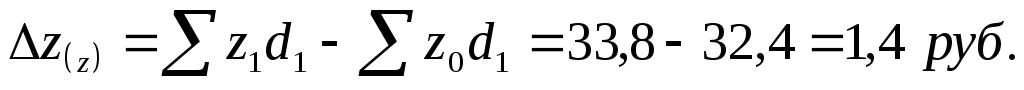
в) 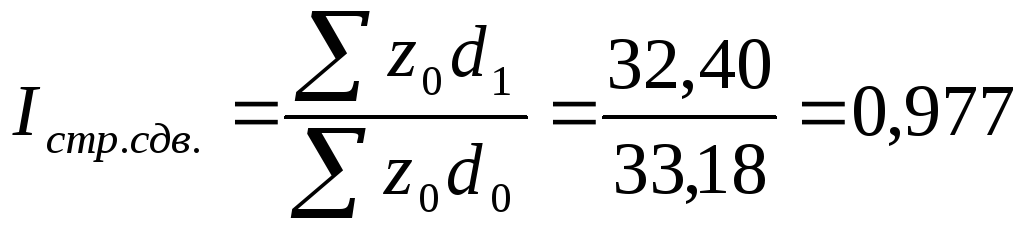
За счет изменений в распределении продукции по комбинатам себестоимость производства кирпича в среднем снизилась на 2,3 %, что в абсолютном размере составило:
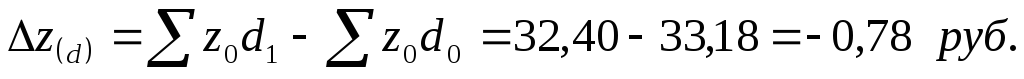
Между вычисленными индексами определим взаимосвязь:
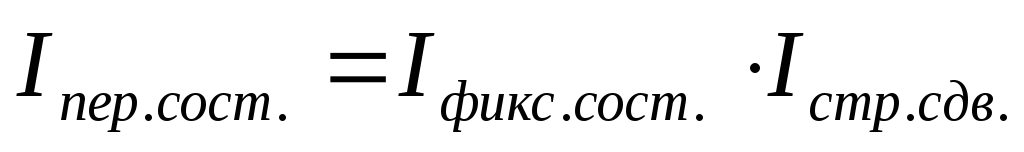
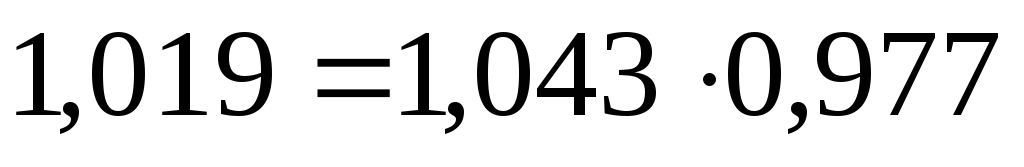
Таким образом, абсолютное изменение себестоимости производства кирпича на комбинатах города за счет роста себестоимости на каждом ДСК и за счет улучшения в распределении продукции (удельного веса) составило:
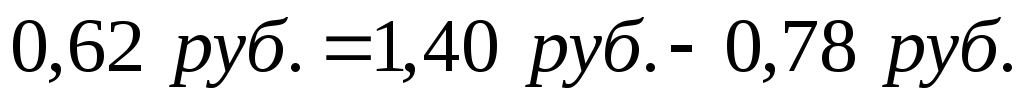
Задание 3
По товарной бирже имеются следующие данные о реализации грузовых автомобилей.
| Марка автомобиля | Стоимость реализованной продукции в базисном периоде, млн. руб.
| Изменение физического объема реализации в текущем периоде по сравнению с базисным, % |
| МАЗ-5551 | 7,36 | -2,6 |
| КамАЗ-55111 | 15,20 | +3,1 |
| КамАЗ-53212 | 9,00 | -0,4 |
Определите:
индекс физического объема реализованной продукции товарной биржи;
сводный индекс изменения товарооборота при реализации, если известно, что цены на грузовые автомобили возросли на 7%;
абсолютный прирост стоимости реализованной продукции за анализируемый период.
Решение
Для определения изменения физического объема реализации в целом по товарной бирже используется формула среднего арифметического индекса, так как по условию известно изменение физического объема реализации(%):
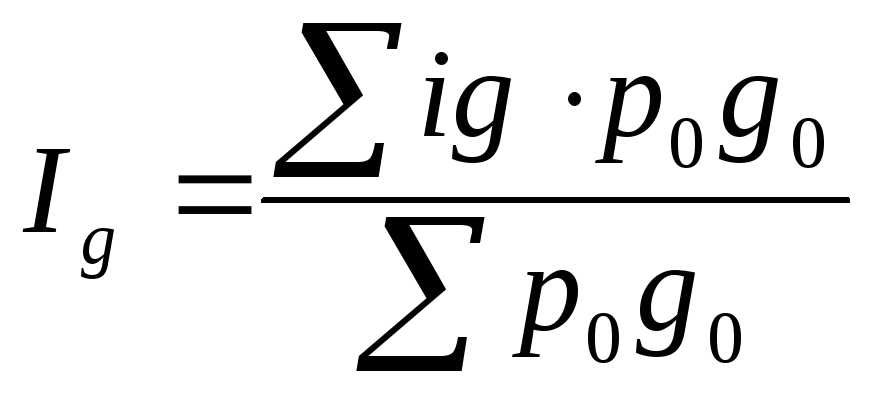 ,
,
где  - индивидуальный индекс физического объема, характеризующий изменение физического объема отдельного вида продукции в текущем периоде по сравнению с базисным.
- индивидуальный индекс физического объема, характеризующий изменение физического объема отдельного вида продукции в текущем периоде по сравнению с базисным.
индивидуальные индексы физического объема по маркам автомобилей следующие:
МАЗ-5551 – 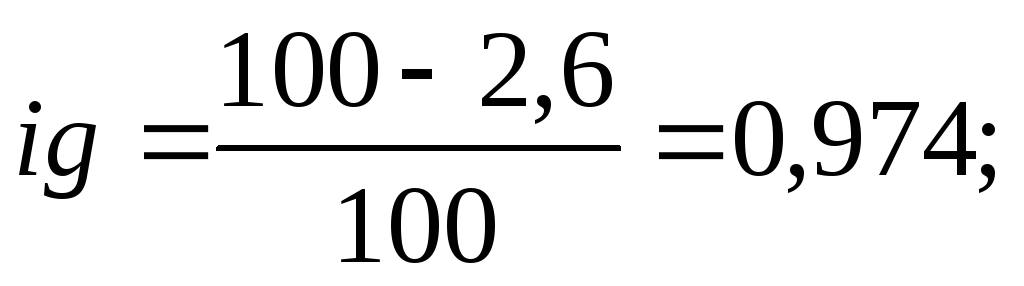
КамАЗ-55511 – 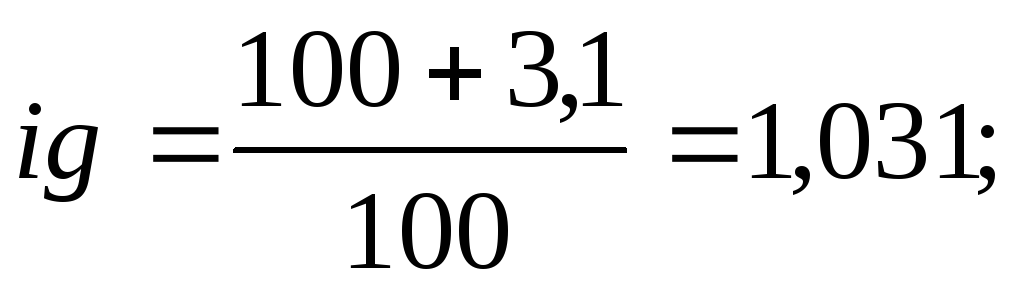
КамАЗ-53212 – 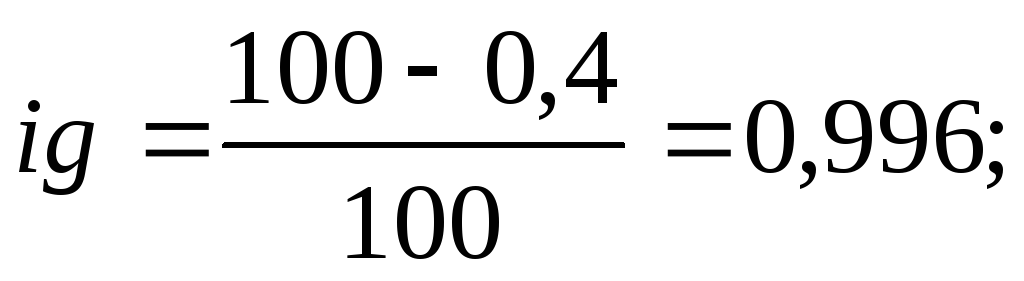
получаем 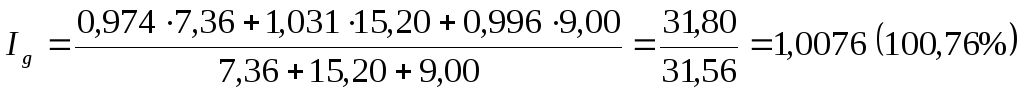
Следовательно, физический объем реализации грузовых автомобилей увеличился на 0,76%, что в денежном выражении составило 240 тыс. руб.
Так как по условию задания известно, что цены на грузовые автомобили возросли на 7%, то можно определить, как изменился общий товарооборот:
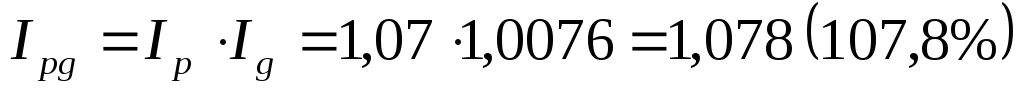
т.е товарооборот увеличился по данной товарной бирже на 7,8%.
Полученные результаты позволяют утверждать, что при реализации грузовых автомобилей в отчетном периоде в связи с возросшим физическим объемом реализованной продукции на 0,76% товарная биржа получила дополнительно за счет этого 240 тыс. рублей. В связи с тем, что в анализируемом периоде отмечен и рост цен (на 7%), то оба этих факта, естественно, привели к росту товарооборота грузовых автомобилей на 7,8%. Таким образом, стоимость реализованной продукции в отчетном периоде составила 34,02 млн. руб. Следовательно, рассмотренные факторы позволили товарной бирже увеличить стоимость реализованной продукции в отчетном периоде по сравнению с базисным на 2,46 млн. руб.
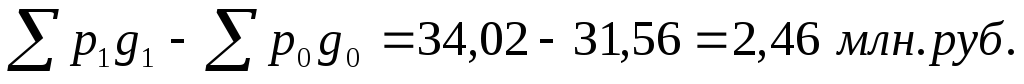
Задание 4
Имеются следующие данные по группе сельскохозяйственных предприятий района:
| Хозяйство | Затраты на производство продукции в отчетном периоде, млн. руб.
| Изменение затрат на единицу продукции по сравнению с базисным периодом, % |
| 1 | 167,0 | -2,3 |
| 2 | 220,0 | +4,1 |
| 3 | 158,8 | +1,8 |
| 4 | 250,0 | -0,9 |
Определите:
индекс затрат на единицу продукции по совокупности сельскохозяйственных предприятий;
сводный индекс изменения затрат на производство, если физический объем производства по группе предприятий сократился на 4 %;
сумму экономии (перерасхода) затрат в отчетном периоде по сравнению с базисным, в т.ч. в связи с изменением себестоимости производства сельскохозяйственной продукции.
Решение
Индекс затрат на единицу продукции (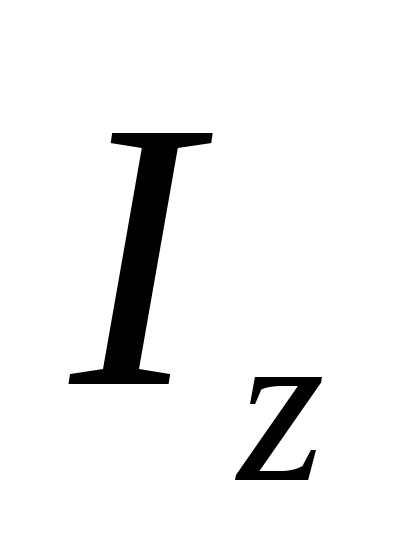 )определяется как средний гармонический индекс:
)определяется как средний гармонический индекс:
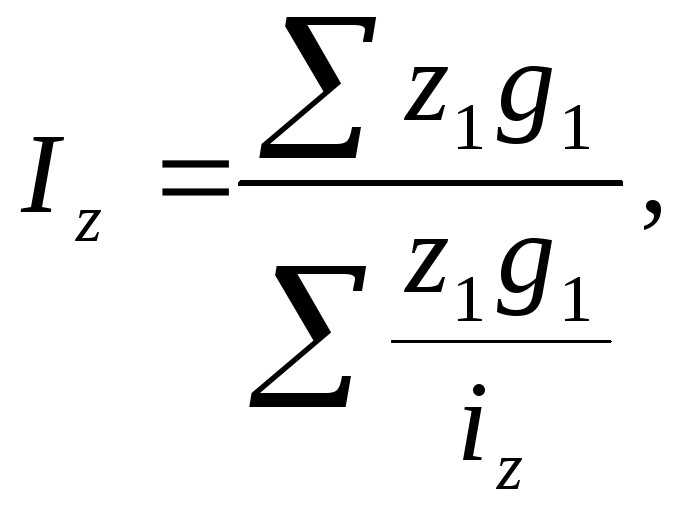
где 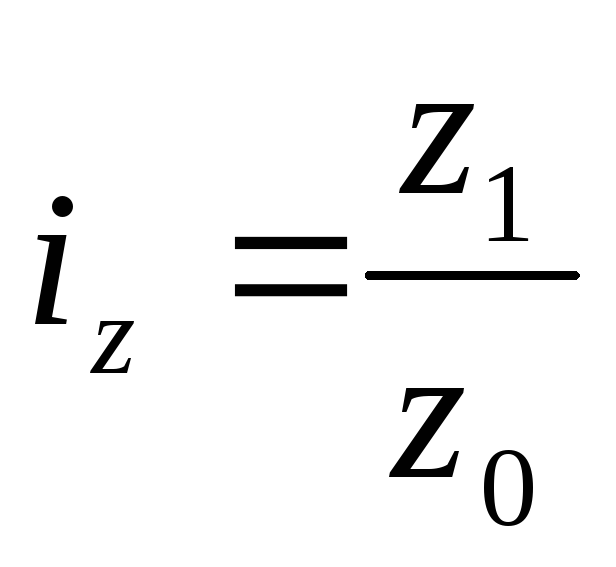 - индивидуальный индекс себестоимости, характеризующий изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным.
- индивидуальный индекс себестоимости, характеризующий изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным.
Таким образом, имеющиеся данные, представленные в процентном выражении, переведем в коэффициенты.
Получаем: -2,3% = 0,977;
+4,1% = 1,041 и т.д.
Отсюда 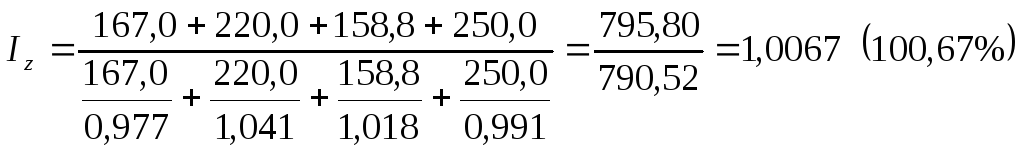
Следовательно, затраты на единицу продукции (z) по совокупности сельскохозяйственных предприятий в текущем периоде по сравнению с базисным в среднем возросли на 0,67%.
Разность числителя и знаменателя показывает сумму перерасхода предприятий в связи с изменением (ростом) себестоимости на производство сельскохозяйственной продукции.
В денежном выражении перерасход равен:
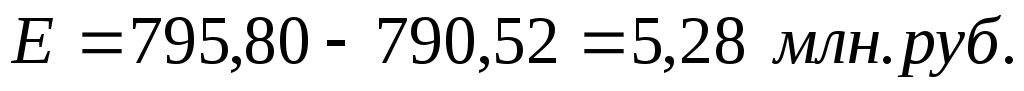
Если известно, что физический объем производства по группе предприятий сократился на 4 %, то можно определить, как изменились в целом затраты на производство в отчетном периоде:
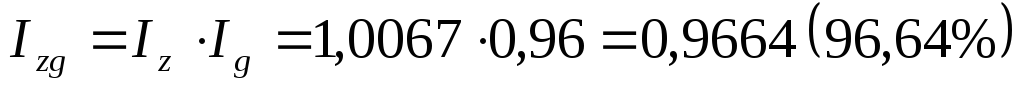
Так как затраты на производство сельскохозяйственной продукции в базисном периоде были на 3,36% выше (100,0 - 96,64), то они равнялись 823,47 млн. руб.
В результате проведенных расчетов, мы выявили, что по группе анализируемых сельскохозяйственных предприятий в отчетном периоде по сравнению с базисным рост себестоимости производства продукции на 0,67% повлек за собой увеличение общих затрат на 5,28 млн. руб. Что, вероятно, в свою очередь послужило толчком к снижению объемов производства сельскохозяйственной продукции на 4%. В целом же, изменение этих факторов (g, z) привели к тому, что затраты на производство продукции в отчетном периоде сократились на 27,67 млн. руб.
studfiles.net
Структурные характеристики ряда распределения
К структурным характеристикам ряда распределения относят медиану и моду. Они не зависят от крайних значений вариантов, поэтому применяются для характеристики центра в ряду распределения с неопределенными границами.
4.2.1. Медиана (Me) - это значение признака, приходящееся на середину упорядоченной совокупности.
Её используют как наиболее надежный показатель типичного значения признака в неоднородной совокупности (включающей резкие отклонения от 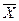 ).
).
Медиана находит широкое практическое применение также вследствие особого математического свойства: сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:
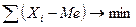
Медиана (Ме) соответствует варианту, стоящему в середине ранжированного ряда.
Положение медианы определяется ее номером по формуле:
N 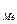 =
=  ,
,
где:
n – число единиц в совокупности.
Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.
Численное значение медианы для интервального ряда определяется по формуле:
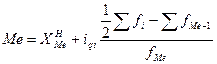 , где:
, где:
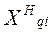 — нижняя граница интервала, в котором находится медиана;
— нижняя граница интервала, в котором находится медиана;
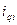 — величина интервала;
— величина интервала;
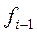 — сумма накопленных частот интервалов, предшествующих интервалу, в котором находится медиана;
— сумма накопленных частот интервалов, предшествующих интервалу, в котором находится медиана;
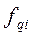 — частота интервала, в котором находится медиана.
— частота интервала, в котором находится медиана.
4.2.2. Мода (Мо) – это варианта, соответствующая наибольшей частоте или варианте, которая встречается наибольшее количество раз.
В дискретном ряду мода определяется визуально по максимальной частоте (f) или частости.
В интервальном ряду модальный интервал определяется по наибольшей частоте, т.е. это тот интервал, который имеет наибольшую частоту, а конкретное значение моды в интервале вычисляется по формуле:
Мо = х0 + i 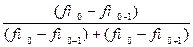 , где:
, где:
Х0 –нижняя граница модального интервала,
i - величина модального интервала,
fM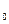 , fM
, fM , fM
, fM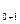 - частоты (частости) модального, предмодального и послемодального интервалов.
- частоты (частости) модального, предмодального и послемодального интервалов.
Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды.
Если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариант больше двух, то ряд – полимодальный.
Мода так же, как и медиана, не требует знания всех индивидуальных значений признака и поэтому может быть использована в качестве наиболее типичного значения признака в неоднородной совокупности.
На практике мода и медиана часто используются вместо средней арифметической или наряду с ней. Так, фиксируя средние цены на оптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т.е. определяют моду цены. Тем не менее, наилучшей характеристикой величины варианта служит средняя арифметическая, которая имеет ряд существенных преимуществ, главное из которых – точное отражение суммы всех значений признака, использующихся для решения соответствующих практических задач.
Решение типовых задач
4.3.1.За январь имеются следующие данные о заработной плате продавцов по четырем секциям торгового дома:
| секции | заработная плата, рублей x | количество продавцов f | фонд оплаты труда, рублей xi fi |
| Итого |
Вычислитесреднюю месячную заработную плату по четырем секциям в целом.
Решение:
Обозначим заработную плату через x, а количество продавцов через f. Логическая формула средней величины имеет следующий вид:
Средняя заработная плата= 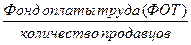
Фонд оплаты труда (ФОТ) каждой секции представляет собой произведение заработной платы на количество продавцов этой секции,
т.е. 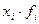 .
.
Чтобы определить ФОТ по всему торговому предприятию, необходимо исчислить фонды по каждой секции, затем их суммировать.
Средняя заработная плата одного продавца в целом по торговому предприятию за месяц будет равна отношению этой суммы и численности продавцов всех секций.
Так как ФОТ равен произведению варианты на частоту, то, в этом случае, для определения средней величины применяется формула средней арифметической взвешенной. Обоснованную логическую формулу выразим алгебраически через соответствующие обозначения:
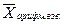 =
= 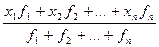 =
= 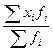 , где:
, где:
x 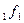 - ФОТ первой секции,
- ФОТ первой секции,
f1- численность продавцов первой секции,
x2f2 - ФОТ второй секции,
f2- численность продавцов второй секции и т.д.
Теперь произведем расчет средней заработной платы одного продавца по формуле средней арифметической взвешенной:
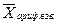 =
= 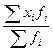 =
=  =
= 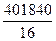 = 25115 руб.
= 25115 руб.
Средняя заработная плата одного продавца, рассчитанная по формуле средней арифметической взвешенной, за январь равна 25115 руб.
Какой экономический смысл заключается в формуле средней арифметической взвешенной?
В числителе вполне определенная величина: ФОТ; в знаменателе – численность всех продавцов. Отношение числителя и знаменателя дает среднюю величину. Важно подчеркнуть это обстоятельство для того, чтобы уяснить экономическую связь между реальными показателями и средней взвешенной величиной. Она связана с общим размером ФОТ: если среднюю величину 25115 руб. умножить на число продавцов 16, то должны получить общий размер фонда оплаты труда (25115*16=401840 руб.).
ФОТ – величина, которая является определяющим показателем и от которой зависят форма и величина средней величины.
4.3.2.По данным таблицы требуется определить средний процент студентов университета, направленных на обучение организациями:
| отделение университета | всего студентов, чел. | из них, направленные на обучение организациями, % |
| заочное | ||
| очное | ||
| Итого |
Решение:
Вариантами (х) в данном случае являются проценты направленных студентов на обучение организациями потребительской кооперации, а весами или частотами (f) – количество студентов на каждом отделении.
Средний процент направленных студентов на обучение кооперативными организациями в целом по университету равен:
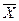 =
= 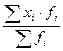 =
= 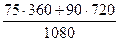 =
= 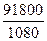 = 85%
= 85%
4.3.3.За два месяца по предприятиям района имеются следующие данные:
| № предприятия | сентябрь | октябрь | ||
| численность работников | средняя месячная заработная плата, руб. | средняя месячная заработная плата, руб. | фонд заработной платы, руб. | |
Определите, за какой месяц и на сколько процентов была выше средняя месячная заработная плата работников предприятия.
Решение:
Введем условные обозначения для сентября:
f - численность работников по каждому предприятию;
x- средняя месячная заработная плата работников каждого предприятия.
Определяющий показатель – общий фонд заработной платы - 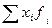 .
.
Средняя месячная заработная плата работников предприятия за сентябрь составила:
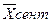 =
= 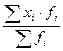 =
= 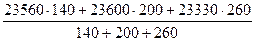 =
=  = 23473,7 руб.
= 23473,7 руб.
Условные обозначения для октября следующие:
w - фонд заработной платы по каждому предприятию;
x – средняя месячная заработная плата работников каждого предприятия.
Определяющий показатель - 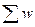 .
.
Средняя заработная плата в октябре исчисляется по формуле средней гармонической взвешенной:
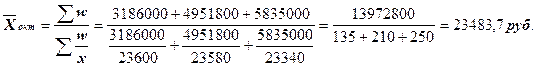
где: 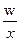 - численность работников каждого предприятия в октябре.
- численность работников каждого предприятия в октябре.
Динамика средней месячной заработной платы работников предприятий:
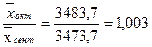 или 100,3%.
или 100,3%.
Следовательно, средняя месячная заработная плата работников предприятий в октябре повысилась на 0,3% по сравнению с сентябрем (100,3% - 100%).
4.3.4. В таблице имеются данные о дневной выработке деталей рабочими цеха (графы 1-2):
(в графах 3-4 данной таблицы уже выполнены предварительные расчеты для решения задачи).
Определите среднедневную выработку рабочих цеха.
Решение:
Так как предварительные расчеты уже сделаны в таблице, то среднедневную выработку рабочими цеха, находим по формуле средней арифметической взвешенной:
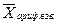 =
= 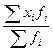 =
= 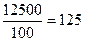 деталей
деталей
Следовательно, рабочие цеха делают в среднем 125 деталей в день.
4.3.5.Определитемоду по данным таблицы:
Распределение размеров женской обуви,
проданных в обувном отделе торгового объединения, в ноябре 2010 г.
| размер женской обуви (х) | число проданных пар, % к итогу (f) |
| А | |
| Итого |
Решение:
По данным таблицы видно, что наибольшая частость (f =26) приходится на 36-й размер обуви.
Следовательно, мода (Мо) равна 36-му размеру, т.е. в данной совокупности именно этот размер обуви в ноябре 2010 года пользовался наибольшим спросом у женского населения.
4.3.6.По данным о содержании влаги в поступившей партии товара в магазин, определите моду:
| влажность, % (х) | число образцов (f) | накопленная частота S | середина интервала x 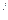  | x 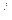 f f
|
| А | ||||
| до 14 | ||||
| 14-16 | ||||
| 16-18 | ||||
| 18-20 | ||||
| 20 и более | ||||
| Итого | - | - |
Решение:
По данным таблицы, наибольшей влажностью обладают товары в интервале 14 - 16% (графа 1). Это и есть модальный интервал, величина интервала i = 2 (16 - 14), нижняя граница х 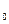 = 14, частота fМо = 30, предмодальная частота fМо-1 = 20, а послемодальная частота fМо+1 = 25.
= 14, частота fМо = 30, предмодальная частота fМо-1 = 20, а послемодальная частота fМо+1 = 25.
Модальный процент влажности в партии товара составляет:
Мо = х0 + i 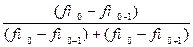 = 14 + 2
= 14 + 2 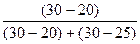 =15,3%
=15,3%
Таким образом, в данной совокупности поступившей партии товаров наибольший процент влажности приходится на 15,3%.
4.3.7.Определите медиану интервального ряда по данным о содержании влаги в поступившей партии товара в магазин:
| влажность, % (х) | число образцов (f) | накопленная частота S |
| А | ||
| до 14 | ||
| 14-16 | ||
| 16-18 | ||
| 18-20 | ||
| 20 и более | ||
| Итого | - |
Решение:
Для определения медианы в интервальном ряду сначала находим номер медианы:
N = 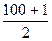 = 50,5%
= 50,5%
Накапливаем частоты (графа 2 таблицы) и определяем, что 50,5 образцов товара приходится на интервал (16 – 18).
Точное нахождение медианы на данном интервале определим по формуле:
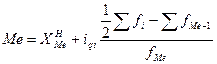 = 16+2
= 16+2 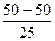 = 16%
= 16%
Таким образом, половина (50%) партии товара имеет влажность менее 16%, и половина (50%) имеет содержание влаги в партии товара выше 16%.
4.4. Задания для самостоятельной работы
Задача 1.
Оборот розничной торговли предприятия в первом квартале составил: за январь – 1280 млн.руб.; за февраль – 1260 млн.руб.; за март – 1320 млн.руб.
Определите среднемесячный оборот розничной торговли предприятия.
Укажите вид применяемой средней величины.
Задача 2.
Вычислитесреднемесячную заработную плату рабочих по хлебозаводу в целом на основании следующих данных:
| название цеха | количество рабочих, человек | среднемесячная заработная плата, руб. |
| хлебобулочный | ||
| кондитерский | ||
| безалкогольных напитков |
Укажите вид применяемой средней величины, напишите ее формулу.
Задача 3.
Рассчитайте средний стаж работы продавцов магазина «Универмаг» на основании следующих данных:
| стаж работы, лет | численность работников, чел. |
Укажите вид применяемой средней величины, напишите ее формулу.
Задача 4.
Определитесредний настриг шерсти в расчете на 1 овцу на основании следующих данных по сельскохозяйственным предприятиям:
| ООО «Победа» | ООО «Скат» | ||
| настриг на 1 овцу, кг | количество овец, шт | настриг на 1 овцу, кг | валовой настриг, кг |
Укажите вид применяемых средних величин. Напишите их формулы.
Задача 5.
Рассчитайтесредний размер пенсии на основании следующих данных:
| группы пенсионеров по размеру пенсий, рублей | число пенсионеров, человек |
| до 4500 | |
| 4501-6000 | |
| 6001-7500 | |
| 7501-9000 | |
| свыше 9000 |
Укажите вид применяемых средних величин. Напишите их формулы.
Задача 6.
По данным, полученным в результате изучения спроса на женскую обувь, определитемоду и медиану:
Размер обуви (х)22 22,5 23 23,5 24 24,5 25 25,5 26
Число пар (f ) 10 48 157 154 182 76 93 98 57
Задача 7.
По результатам зимней экзаменационной сессии одного курса студентов получено следующее распределение оценок по баллам:
| балл оценки знаний студентов | Итого | ||||
| число оценок, полученных студентами |
Определите:
а) средний балл оценки знаний студентов;
б) модальный балл успеваемости и медианное значение балла;
в) сделайте выводы о характере данного распределения.
Задача 8.
Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| товарооборот, млн. руб. | до 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
| число фирм |
Определите:
а) средний размер месячного товарооборота на одну фирму;
б) модальное и медианное значение месячного товарооборота;
в) сделайте выводы о характере данного распределения.
Задача 9.
Распределение предприятий по показателю затрат на 1 тыс. руб. продукции в октябре следующее:
| затраты на 1 тыс. руб. продукции, руб. | число предприятий | общая стоимость продукции, тыс. руб. |
| 600-650 | ||
| 650-700 | ||
| 700-750 | ||
| 750-800 |
Определите:
1) средний размер затрат на 1 тыс. руб. продукции по предприятиям;
2) средний объем продукции на одно предприятие.
Задача 10.
Имеются следующие данные об экспорте продукции:
| вид продукции | удельный вес продукции на экспорт, % | стоимость продукции на экспорт, млн. руб. |
| сталь арматурная | 40,0 | |
| прокат листовой | 32,0 |
Определите средний удельный вес продукции на экспорт.
Задача 11.
Имеются следующие данные о квалификации рабочих двух бригад:
| № бригады | число рабочих | уровень квалификации каждого рабочего бригады (тарифный разряд) | |||||||||||
Определите средний уровень квалификации рабочих каждой бригады.
Задача 12.
Продажа грузовых автомобилей КамАЗ-55111 на товарной бирже города характеризуется следующими данными:
| дата торга | реализовано автомобилей, шт. | средняя цена одного автомобиля, тыс. руб. | дата торга | общая сумма выручки от реализации автомобилей, тыс. руб. | средняя цена одного автомобиля, тыс. руб. |
| 4. 01 | 1200,5 | 3. 02 | 1220,0 | ||
| 17. 01 | 1180,7 | 9. 02 | 1200,5 | ||
| 28. 01 | 1160,0 | 20. 02 | 1190,0 | ||
| 26. 02 | 1230,2 |
Определите, на сколько процентов изменилась средняя цена одного грузового автомобиля в феврале по сравнению с январем.
Задача 13.
Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее:
| суточный пробег автомобиля, км | до 160 | 160-180 | 180-200 | 200 и более |
| число автомобилей |
Определитесредний суточный пробег одного автомобиля.
Задача 14.
По двум цехам имеются следующие данные о распределении рабочих по уровню месячной заработной платы за апрель:
| месячная заработная плата, руб. | число рабочих | месячная заработная плата, руб. | число рабочих | ||
| цех №1 | цех №2 | цех №1 | цех №2 | ||
| 18000-18400 | 19200-19600 | ||||
| 18400-18800 | 19600-20000 | ||||
| 18800-19200 |
Определите, в каком цехе и на сколько процентов была выше средняя заработная плата рабочих.
Задача 15.
Автобус на междугородной линии протяженностью 625 км прошел путь в прямом направлении со скоростью 68 км/ч, в обратном направлении – со скоростью 52 км/ч.
Определитесреднюю скорость сообщения за обратный рейс.
Задача 16.
Имеются следующие данные по предприятиям фирмы:
| № предприятия, входящего в фирму | I квартал | II квартал | ||
| выпуск продукции, тыс. руб. | средняя выработка на одного рабочего в день, руб. | отработано рабочими, человеко-дней | средняя выработка 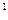 на одного рабочего в день, руб. на одного рабочего в день, руб.
| |
| 59390,13 | 1540,6 | 1600,4 | ||
| 34246,10 | 1421,0 | 1500,0 | ||
| 72000,00 | 1600,0 | 1621,0 | ||
 Средняя выработка на одного рабочего в день определяется путем деления общей стоимости продукции на количество отработанных человеко-дней. Средняя выработка на одного рабочего в день определяется путем деления общей стоимости продукции на количество отработанных человеко-дней.
|
Определите:
1) среднюю выработку на одного рабочего в день в целом по фирме в I и II кварталах;
2) на сколько процентов изменилась средняя выработка на одного рабочего в день во II квартале по сравнению с I кварталом;
3) среднюю выработку на одного рабочего в день по фирме за первое полугодие.
Задача 17.
По металлургическому заводу имеются следующие данные об экспорте продукции:
| вид продукции | стоимость всей реализованной продукции, млн. руб. | удельный вес продукции на экспорт, % |
| чугун | 35,5 | |
| прокат листовой | 22,8 |
Определите средний удельный вес продукции на экспорт.
Задача 18.
Распределение промышленных предприятий региона по показателям затрат на 1 тыс. руб. продукции за два месяца следующее:
| затраты на 1 тыс. руб. продукции, рублей | март | апрель | ||
| число предприятий | общая стоимость продукции, млн. руб. | число предприятий | средний объем продукции на одно предприятие, млн. руб. | |
| 600-650 | ||||
| 650-700 | ||||
| 700-750 |
Определите:
1) изменение (в %) среднего размера затрат на 1 тыс. руб. продукции по предприятиям региона;
2) средний объем продукции на одно предприятие в марте и в апреле.
Задача 19.
Имеются следующие данные о забастовках в Российской Федерации:
| год | число организаций, на которых проходили забастовки | численность работ-ников, участвовав-ших в забастовках, тыс.чел. | количество времени, не отработанного участво-вавшими в забастовках работниками,тыс.чел.дней |
| 369,3 | 1932,2 | ||
| 951,4 | 6171,5 | ||
| 12,6 | 48,8 |
Рассчитайте для каждого года:
1. среднюю численность работников, участвовавших в забастовках, в расчете на одну организацию;
2. средние потери рабочего времени в расчете на одну организацию;
3. средние потери рабочего времени в расчете на одного участника забастовки.
Сформулируйте выводы.
Задача 20.
Имеются следующие данные по фермерским хозяйствам области:
| группы хозяйств по себестоимости 1 центнера сахарной свеклы, руб. | число хозяйств | валовой сбор в среднем на 1 хозяйство, центнеров |
| до 22 22-24 24-26 26 и более | 112,3 97,2 116,4 132,6 |
Определите среднюю себестоимость 1 ц свеклы в целом по фермерским хозяйствам области.
Задача 21.
По результатам обследования сельскохозяйственных предприятий области получены следующие данные:
| группы сельскохозяйственных предприятий по среднему годовому надою молока от одной коровы, кг | число сельскохозяйственных предприятий | среднегодовое поголовье коров (на 1 сельскохозяйственное предприятие) | процент жира в молоке |
| до 2000 2000 – 2200 2200 – 2400 2400 и более | 3,0 3,4 3,7 3,1 |
Определите средний надой молока и среднюю жирность на 1 корову.
Задача 22.
Цехом произведены бракованные детали в трех партиях:
в первой партии – 90 шт., что составило 3,0% общего числа деталей;
во второй партии- 140 шт., или 2,8%;
в третьей партии – 160 шт., или 2,0%.
Определитесредний процент бракованных деталей.
Задача 23.
В отделе заказов торговой фирмы занято четверо работников, имеющих 8-часовой рабочий день. Первый работник на оформление заказа в среднем затрачивает 14 минут, второй 15 минут. Третий 12 минут, а четвертый 19 минут.
Определите средние затраты времени на один заказ в целом по отделу.
Задача 24.
Имеются следующие данные об успеваемости студентов вуза:
| номер факультета | доля отличников в общей численности студентов факультета | доля студентов в общей численности вуза |
| 0,09 0,06 0,15 0,11 | 0,20 0,43 0,08 0,29 |
Определите долю отличников в общей численности студентов.
??? ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое средние величины, какова их роль и значение?
2. Какие существуют средние величины?
3. Как рассчитываются средние арифметические величины?
4. Особенности расчета средней арифметической величины по данным интервального ряда?
5. Как рассчитываются средние гармонические величины?
6. Средняя геометрическая величина и ее расчет?
7. Средняя квадратическая величина и её исчисление?
8. Средняя кубическая величина и её расчет?
9. Общая формула степенных средних величин?
10. Структурные характеристики рядов распределения?
11. Сущность моды и как она рассчитывается для вариационного ряда?
12. Особенность исчисления моды в интервальном ряду распределения?
13. Медиана, ее свойства и способ исчисления для интервального ряда?
14. Свойство мажорантности средних?
15. Что такое бимодальный и полимодальный вариационные ряды распределения?
infopedia.su
Рабочая тетрадь по Статистике - Стр 3
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Задача 17. По итогам года на предприятии с численностью работников 450 человек были собраны следующие сведения о заработной плате работников:
Таблица 12 – Данные о заработной плате работников предприятия
Заработная плата работников, руб. | Число работников, чел. |
До 2000 | 20 |
2000-3000 | 25 |
3000-4000 | 34 |
4000-5000 | 45 |
5000-6000 | 84 |
6000-7000 | 98 |
7000-8000 | 73 |
8000-9000 | 41 |
9000-10000 | 18 |
Более 10000 | 12 |
Определите среднюю заработную плату на предприятии, а также среднюю модальную и среднюю медианную заработную плату.
Порядок выполнения работы:
1) Среднюю заработную плату на предприятии определим по формуле средней арифметической взвешенной, для вычисления которой подготовим расчётную таблицу 13.
Таблица 13 – Исходные и расчётные данные для вычисления средней зарплаты
Заработная плата | Середина | Число работников, | Произведение Хf |
работников, руб. | интервалов (Х) | чел. (f) |
|
До 2000 |
|
|
|
2000-3000 |
|
|
|
3000-4000 |
|
|
|
4000-5000 |
|
|
|
5000-6000 |
|
|
|
6000-7000 |
|
|
|
7000-8000 |
|
|
|
8000-9000 |
|
|
|

9000-10000
Более 10000
Итого: –
Данные из таблицы подставим в формулу и вычислим искомую среднюю заработную плату:
f
f =
2)Определим модальную и медианную заработную плату. Для этого сначала необходимо установить модальный интервал (интервал с наибольшей частотой), а затем вычислим:
а) модальную заработную плату по формуле:
Мо | Х о | i |
|
| ( f2f1) |
|
|
| |
( f | 2 | f ) (f | 2 | f | ) = | ||||
|
|
|
| 1 | 3 |
|
| ||
где: Хо – нижняя граница модального интервала;i – величина интервала;
f1 – частота интервала, предшествующего модальному;f2 – частота модального интервала;
f3 – частота интервала, следующего за модальным.
б) вычислим медианную заработную плату: | ||||
| f | Sx | ||
М е Хо i | 2 | |||
|
| |||
| = | |||
| fM | |||
где: Хо – нижняя граница медианного интервала; i – величина интервала;
S x – накопленная частота до медианного интервала;
f – сумма частот всей совокупности;f M – частота медианного интервала.
3) Выводы:
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________

Задача 18. По данным таблицы 14 определите среднюю площадь посева в сельхозпредприятиях, среднюю урожайность и среднюю стоимость 1 ц озимой пшеницы. Сделайте выводы.
Таблица 14 – Исходные и расчётные данные для вычисления средних величин
|
| Исходные данные |
| Расчетные данные | |||
№ | Посевная |
| Урожайность | Себестоимость | Валовой | Общие | |
площадь, га |
| сбор, ц (УS), | затраты, тыс. | ||||
|
| ц/га (ц). (У) | 1ц, руб. (Z) | ||||
| (S) |
| (f) | руб. (Zf) | |||
|
|
|
|
| |||
1 | 1234 |
| 29,4 |
| 172 |
|
|
2 | 5617 |
| 32,1 |
| 130 |
|
|
3 | 3850 |
| 30,7 |
| 144 |
|
|
4 | 2619 |
| 25,8 |
| 186 |
|
|
5 | 1714 |
| 34,2 |
| 119 |
|
|
Итого: |
|
| – |
| – |
|
|
Порядок выполнения задания:
1) Определим среднюю посевную площадь на СХП по формуле средней арифметической простой:
S S = n
2) Вычислим среднюю урожайность 1 ц озимой пшеницы средней арифметической взвешенной:
YYS
S =
3) Вычислим среднюю себестоимость 1 ц озимой пшеницы по формуле средней арифметической взвешенной:
ZZf
f =
Выводы:
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
23

Задача 19. Имеются данные о производстве зерновых культур в сельхозпредприятии за 2 периода (таблица 15). Определите среднюю урожайность зерновых культур в отчетном и базисном периодах.
Таблица 15 – Исходные данные для расчета средней урожайности
| Базисный период | Отчетный период | |||
Культуры | Урожайность, | Валовой | Урожайность, | Посевная | Валовой |
площадь, га | |||||
| ц/га (Y0) | сбор, ц (W) | ц/га (Y1) | (S) | сбор, ц (Y1S) |
|
|
|
|
| |
Озимая | 23,5 | 28200 | 29,1 | 1570 |
|
пшеница |
| ||||
|
|
|
|
| |
Ячмень | 18,2 | 10920 | 22,3 | 720 |
|
яровой |
| ||||
|
|
|
|
| |
Кукуруза на | 32,8 | 8200 | 30,4 | 390 |
|
зерно |
| ||||
|
|
|
|
| |
Овес | 12,8 | 1920 | 14,7 | 160 |
|
Итого: | – |
| – |
|
|
Порядок выполнения задания:
1) Определим среднюю урожайность в отчётном периоде по формуле средней арифметической взвешенной:
YY1S
S =
2) Вычислим среднюю урожайность в базисном периоде. Для этого необходимо валовой сбор разделить на посевную площадь. Так как у нас нет данных о размере посевных площадей, а, следовательно, отсутствует знаменатель для средней арифметической взвешенной, то для определения средней урожайности сначала установим размер посевной площади отдельно по каждой культуре. Для этого валовой сбор каждой культуры разделим на её урожайность, т.е. найдём искомый знаменатель средней арифметической, а затем обычным порядком определим среднюю урожайность по формуле средней гармонической взвешенной:
Уг арм W
WУ=
где: У – урожайность отдельных культур в базисном году, ц/га;W – валовой сбор отдельных культур в базисном году, ц.
3) Выводы:

____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Задача 20. Используя данные таблицы 16, для двух предприятий определите следующие показатели:
среднюю выработку на одного рабочего за смену;
среднюю прогрессивную выработку;
размах вариации;
среднее линейное отклонение;
дисперсию;
среднее квадратичное отклонение;
коэффициент вариации.
Сравните полученные данные и сделайте выводы.
Таблица 16 – Выработка продукции на 1 рабочего за смену
№ |
|
|
| Выработка на 1 рабочего за смену, руб. |
|
|
| |||||||
1 | 40 | 45 | 58 | 60 | 52 | 53 | 44 | 62 | 55 | 48 | 38 | 49 | 59 | 50 |
2 | 39 | 54 | 49 | 46 | 48 | 57 | 52 | 43 | 59 | 56 | 50 | 41 | 47 | 45 |
Порядок выполнения задания:
1) Определим среднюю выработку на одного рабочего за смену по формуле средней арифметической простой:
Х Х ,
п
а) на первом предприятии: Х 1
б) на втором предприятии: Х 2
2) Вычислим среднюю прогрессивную выработку на одного рабочего (это средняя из выработок выше средней величины), также по формуле средней арифметической простой:
Х Х ,
п
а) на первом предприятии: Х 1
б) на втором предприятии: Х 2
3) Размах вариации:

R = Хmах – Хmin
а) на первом предприятии: R1 =
б) на втором предприятии: R2 =
4) Среднее линейное отклонение (невзвешенное):
|
|
|
| х |
|
|
|
|
|
| х |
|
| ||
е |
|
|
|
|
|
| |
|
| n | , | ||||
|
|
|
| ||||
|
|
|
|
|
| ||
а) на первом предприятии: е1
б) на втором предприятии: е2
5) Дисперсия: 2 x x 2
n
а) на первом предприятии: 12
б) на втором предприятии: 22
6) Среднее квадратическое отклонение:
,
|
|
|
|
|
|
| |
|
|
| x |
| 2 |
| |
|
|
| x |
| |||
| 2 |
| , | ||||
n | |||||||
|
|
| |||||
|
|
|
| ||||
а) на первом предприятии: 1
б) на втором предприятии: 1
7) Коэффициент вариации: 100% ,
Х
а) на первом предприятии: v1 =
б) на втором предприятии: v2 =
8) Выводы:
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Задача 21. В результате анализа 500 проб получены данные о проценте влажности зерна:

Таблица 17 – Исходные данные о влажности зерна
Влажность зерна, % | До 4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 | Итого: |
Число проб, шт. | 41 | 64 | 72 | 132 | 110 | 81 | 500 |
Определите дисперсию по основной формуле и по формуле:
2 Х 2Х 2 .
Порядок выполнения задания:
1) Для определения дисперсии по основной формуле подготовим расчётную таблицу.
Таблица 18 – Данные для расчёта дисперсии
Влажность | Среднее | Число | Х f |
|
|
|
|
|
|
|
|
|
|
|
|
| ( Х Х)2 | (Х Х)2 f | |||||||
значение | Х Х |
| ||||||||||
зерна, % | проб (f) |
| ||||||||||
| интервалов (Х) |
|
|
|
|
|
|
|
|
|
|
|
До 4 | 3 | 41 |
|
|
|
|
|
|
|
|
|
|
4-6 | 5 | 64 |
|
|
|
|
|
|
|
|
|
|
6-8 | 7 | 72 |
|
|
|
|
|
|
|
|
|
|
8-10 | 9 | 132 |
|
|
|
|
|
|
|
|
|
|
10-12 | 11 | 110 |
|
|
|
|
|
|
|
|
|
|
12-14 | 13 | 81 |
|
|
|
|
|
|
|
|
|
|
Итого: | – | 500 |
| – |
| – |
|
|
| |||
2) Средний процент влажности зерна определим по формуле средней арифметической взвешенной:
f
f =
3) Дисперсия по основной формуле:
2 x x 2 f =
f
4)Находим дисперсию по формуле:
|
|
|
|
|
| 2 |
|
| |
2 | Х 2 |
|
| ||||||
Х | = |
| |||||||
|
| 2 |
| Хf | 2 | ||||
|
| ||||||||
| Х |
| f |
| |||||
где: |
| = | |||||||
|
|
|
|
|
| ||||
|
|
| Х 2 f |
|
|
|
|
|
|
| |||
| Х 2 |
|
|
|
|
|
|
| |||||
|
| f | = |
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||||
Для определения Х 2 | составим расчётную таблицу: |
|
|
| |||||||||
|
|
| Таблица 19 – Данные для расчёта дисперсии |
|
| ||||||||
Среднее значение |
| 3 |
| 5 | 7 | 9 | 11 | 13 | Итого | ||||
интервалов (Х) |
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
| |||
Число проб, шт. (f) |
| 41 |
| 64 | 72 | 132 | 110 | 81 | 500 | ||||
Х2 |
|
|
|
|
|
|
|
|
|
|
| ||
Х2∙f |
|
|
|
|
|
|
|
|
|
|
| ||
5) Выводы:
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
Задача 22.
По группе промышленных предприятий, выпускающих одинаковые виды продукции, имеются следующие данные за отчетный год (табл.)
показатель |
|
|
| ПРЕДПРИЯТИЕ |
|
|
| |||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 |
Общий объем | 249, | 391,6 | 734,4 | 512,0 | 369,4 | 806,4 |
| 224,6 | 213,8 | 696,0 |
продукции, млн. руб |
|
|
|
|
|
|
|
|
|
|
Среднесписочная | 520 | 680 | 1020 | 970 | 855 | 1200 |
| 585 | 594 | 1000 |
численность |
|
|
|
|
|
|
|
|
|
|
работников, |
|
|
|
|
|
|
|
|
|
|
чел. |
|
|
|
|
|
|
|
|
|
|
Фондовооруженност | 30,8 | 36,0 | 41,5 | 35,5 | 27,6 | 40,2 |
| 25,5 | 24,0 | 40,8 |
работников, |
|
|
|
|
|
|
|
|
|
|
тыс. руб./ чел. |
|
|
|
|
|
|
|
|
|
|
Для выявления зависимости производительности труда работ Ииников (объема продукции на одного списочного работника) от фондовооруженности (стоимости основных производственных фондов, приходящейся на одного работника) произвести аналитическую группировку предприятий по показателю фондовооруженности труда, выделив три группы предприятий. Интервалы группировки разработать самостоятельно. На основе группировки построить групповую таблицу.
Сформулировать вывод.
Задача 23.
Имеются следующие данные о размере семьи работников цеха (число человек в семье):
3 4 5 2 3 6 4 2 5 3 4 2 7 3 3 6 2 3 8 5 6 7 3 4 5 4 3 3 4
Требуется:
1.составить дискретный вариационный ряд;
2.определить показатели центра распределения, показатели вариации;
3.дать графическое изображение ряда в виде полигона распределения. Сформулировать выводы.
Задача 24.
Имеются следующие данные о возрастном составе группы студентов вечернего отделения ( лет):
18 38 28 29 26 38 34 22 28 30
22 23 35 33 27 24 30 32 28 25
29 26 31 24 29 27 32 25 29 20
Требуется:
1.построить интервальный ряд распределения;
2.дать его графическое изображение в виде гистограммы и кумуляты;
3.определить численное значение моды и медианы, используя графическое изображение.
Задача 25.
По предприятию получены данные о расстоянии перевозки партий груза в междугородном сообщении (км):
560 1060 420 1410 1500 400 3800 700 1780 450
449 285 1850 2200 800 1200 1540 1150 180 452
452 2500 300 400 900 1800 452 1850 1225 220
420 1700 1615 3500 300 320 600 965 450 245
Для анализа работы предприятия требуется:
1.построить интервальный ряд распределения партий груза по дальности перевозки, определив величину интервала по формуле Стерджесса;
2.дать графическое изображение ряда;
3.исчислить показатели центра распределения и показатели вариации. Сформулировать выводы.
Задача 26
Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее (табл.):
Суточный |
|
|
|
|
пробег | До 160 | 160-180 | 180-200 | 200 и более |
автомобиля, |
|
|
|
|
км |
|
|
|
|
Число | 16 | 37 | 22 | 24 |
автомобилей |
|
|
|
|
Определить средний суточный пробег одного автомобиля.
Задача 27.
Продажа грузовых автомобилей КАМАЗ-55111на товарной бирже города характеризуется следующими данными (табл.):
|
|
|
| Общая |
| |
| Реализовано | Средняя |
| сумма | Средняя | |
| вена одного | Дата | выручки т | цена одного | ||
Дата торга | автомобилей | |||||
автомобиля, | торга | реализации | автомобиля, | |||
| шт. | тыс. руб. |
| автомобилей | тыс. руб. | |
|
|
| ||||
|
|
|
| тыс. руб. |
| |
4.01. | 18 | 120,5 | 3.02 | 1830 | 122,0 | |
17.01 | 25 | 118,7 | 9.02 | 2651 | 120,5 | |
28.01 | 24 | 116,0 | 20.02 | 4165 | 119,0 | |
|
|
| 26.02 | 1232 | 123,2 |
Определить, на сколько процентов изменилась средняя цена одного грузового автомобиля в феврале по сравнению с январем.
Контрольные вопросы:
1.Каково место средних величин в системе статистических показателей?
2.Раскройте содержание средних величин.
3.Какие виды средних величин вы знаете?
4.Что такое структурные средние величины?
5.Перечислите математические свойства средних величин.
6.Что такое вариация признака и чем она обусловлена?
7.Какими показателями измеряется вариация?
8.Что характеризует коэффициент вариации?
ТЕМА 5. РЯДЫ ДИНАМИКИ
Содержание практического занятия: Классификация рядов динамики,
вычисление показателей динамического ряда, сглаживание рядов динамики методом скользящей средней и аналитическое выравнивание, графическое изображение динамики явления. Выявление сезонных колебаний. Приведение ряда динамики к одному основанию.
Задача 28. Стоимость основных производственных фондов на предприятии (в сопоставимых ценах) характеризуется следующими данными:
Таблица 20 – Динамика стоимости ОПФ на предприятии
Годы | Стоимость ОПФ, тыс. руб. |
| 30 |
studfiles.net
2.4. Задачи для самостоятельной работы
2.12. Имеются данные о мощности электростанций Украины (на начало года, млн. кВт):
| Группа электростанций | 2001 г. | 2002г. | 2003г. |
| Тепловые Гидроэлектростанции Атомные | 148,4 43,4 20,2 | 148,8 43,4 21,2 | 149,7 44,0 21,2 |
Определить: 1) показатели динамики мощности всех электростанций Украины; 2) показатели структуры мощности электростанций в 2003 г. (расчет с точностью до 0,1%).
2.13. По фирме имеются данные о выпуске продукции за первый квартал:
| № предприятия фирмы | Выпуск продукции по плану, млн. грн. | Процент выполнения плана по выпуску продукции | |
| 1 | 10,0 | 103,5 | |
| 2 | 24,0 | 98,0 | |
| 3 | 42,5 | 106,0 | |
Определить: 1) процент выполнения плана по выпуску продукции в целом по фирме; 2) удельный вес предприятий в общем объеме фактического выпуска продукции (расчет с точностью до 0,1%).
2.14. По металлургическому комбинату имеются следующие данные о выпуске продукции:
| Наименование продукции | Стоимость продукции в фиксированных ценах, млн. грн. | Процент выполнения плана по выпуску продукции, % | ||
| по плану | фактически | |||
| Сталь арматурная Прокат листовой Гнутые профили стальные | 440 500 | 452 208 | 97,0 104,0 | |
Требуется: 1) проставить в таблице недостающие данные; 2) определить процент выполнения плана выпуска продукции в целом по комбинату.
2.15. В прошлом году себестоимость производства грузового автомобиля КамАЗ-55111 составила 70,0 тыс. грн. По плану отчетного года предусматривалось снизить себестоимость на 1400 грн. фактическая себестоимость составила 68,2 тыс. грн. Определить относительные величины планового задания по снижению себестоимости и динамики себестоимости производства автомобиля.
2.16. Планом предусмотрено увеличение объема продукции предприятия против прошлого года на 2,1%. Фактически прирост продукции против прошлого года составил 4,8%. Определить процент выполнения плана по выпуску продукции.
2.17. По плану отчетного года уровень годовой производительности труда работников должен возрасти против прошлого года на 3,0%. План по уровню производительности труда перевыполнен на 2,0%. Определить фактический уровень производительности труда, если известно, что в прошлом году уровень годовой производительности труда составил 170 тыс. грн.
2.18. Предприятие перевыполнило план реализации продукции в отчетном году на 3,8%. Увеличение реализации продукции в отчетном году по сравнению с прошлым составило 5,6%. Определить, каково было плановое задание по росту объема реализации продукции.
2.19. За отчетный квартал потребление топлива на производственные нужды по предприятию следующее: уголь - 1200 т, газ - 380 тыс. м , нефть - 210 т. Определить, какую долю в общем объеме потребленного топлива занимает уголь, если коэффициенты пересчета в условное топливо следующие: уголь - 0,9 т; газ - 1,2 тыс. м
, нефть - 210 т. Определить, какую долю в общем объеме потребленного топлива занимает уголь, если коэффициенты пересчета в условное топливо следующие: уголь - 0,9 т; газ - 1,2 тыс. м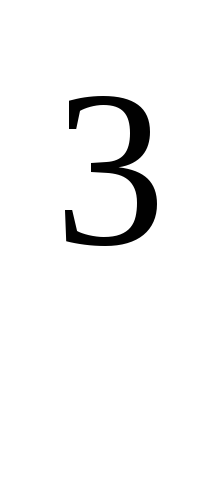 , нефть - 1,3 т.
, нефть - 1,3 т.
2.20. Планом предусмотрено снижение затрат на одну гривну товарной продукции на 4,0%; фактически по сравнению с прошлым годом затраты возросли на 1,8%. Определить, на сколько процентов фактические затраты на одну гривну товарной продукции отличаются от плановых.
2.21. По отделению дороги планом предусмотрено увеличение объема отправок груза на 10,0%. Фактически объем отправок против прошлого года повысился на 12,2%. Определить, на сколько процентов перевыполнен план по объему отправок груза.
2.22. По предприятиям фирмы имеются следующие данные:
| № предприятия, входящего в фирму | Фактический объем реализованной продукции в 2002 г. млн. грн. | Плановое задание по росту реализованной продукции н 2003 г., % | Фактический объем реализованной продукции в 2003 г., млн. грн. | |
| 1 2 3 | 30,0 48.5 60,0 | 104,0 106,0 102,5 | 32,6 52,7 63,0 | |
Определить в целом по фирме:
1) размер планового задания по росту объема реализованной продукции в 2003 г.;
2) процент выполнения плана по объему реализованной продукции в 2003 г.;
3) показатель динамики реализованной продукции.
2.23. Имеются следующие данные о квалификации рабочих двух бригад:
| № бригады | Число рабочих | Уровень квалификации каждого рабочего бригады (тарифный разряд) |
| 1 | 12 | 4; 3; 2; 4; 5; 6; 4; 3; 4; 3; 5; 4; |
| 2 | 10 | 3; 5; 6; 5; 4; 3; 2; 3; 3; 4; |
2.24. Продажа грузовых автомобилей КамАЗ-55111 на товарной бирже города характеризуется следующими данными:
| Дата торга | Реализовано автомобилей, шт. | Средняя цена одного автомобиля, тыс . грн. | Дата торга | Общая сумма выручки от реализации автомобилей, тыс. грн. | Средняя цена одного автомобиля, тыс. грн. |
| 4.01 | 18 | 120,5 | 3.02 | 1830 | 122,0 |
| 17.01 | 25 | 118,7 | 9.02 | 2651 | 120,5 |
| 28.01 | 24 | 116,0 | 20.02 | 4165 | 119,0 |
| 26.02 | 1232 | 123,2 |
Определить, на сколько процентов изменилась средняя цена одного грузового автомобиля в феврале по сравнению с январем.
2.25. Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее:
| Суточный пробег автомобиля, км | До 160 | 160- 180 | 180-200 | 200 и более |
| Число автомобилей | 12 | 36 | 28 | 25 |
Определить средний суточный пробег одного автомобиля.
2.26. По двум цехам имеются следующие данные о распределении рабочих по уровню месячной заработной платы за 1 квартал:
| Заработная плата за 1 кв., грн. | Число рабочих | |
| Цех№1 | Цех №2 | |
| 1000-1200 | 32 | 17 |
| 1200-1400 | 36 | 40 |
| 1400-1600 | 150 | 220 |
| 1600-1800 | 70 | 110 |
| 1800 - 2000 | 32 | 83 |
Определить, в каком цехе и на сколько процентов была выше средняя заработная плата рабочих.
2.27. По двум предприятиям фирмы имеются следующие данные о затратах на производство продукции:
| № предприятия, входящего в фирму | Прошлый год | Отчетный год | ||
| Доля затрат на оплату труда в общих затратах на производство, % | Общие затраты на производство, млн грн. | Затраты на оплату труда, млн грн. | Доля затрат на оплату труда в общих затратах на производство. % | |
| 1 | 18,0 | 200 | 40,7 | 18,5 |
| 2 | 19,5 | 180 | 38,0 | 20,2 |
Определить изменение (в %) доли затрат на оплату труда в общих затратах на производство в целом по фирме в отчетном году по сравнению с прошлым годом.
studfiles.net
Лист Средние
Средние величины Задача 1. Данные о производстве однородной продукции на заводах отрасли. N завода среднегодовая численность рабочих, чел средняя выработка, дет/чел средняя себестоимость 1 детали, руб.151029260
237527255
3104026280
483032240
Определите средние (на 1 завод) величины всех показателей, приведенных в таблице.Укажите вид средней величины, если средняя величина является взвешенной, укажите, что является весом.
Задача 2.Продажа грузовых автомобилей Кам АЗ-55111 на товарной бирже города характеризуется следующими данными:дата торгареализовано автомобилей, шт.средняя цена одного автомобиля, тыс. руб.дата торгаобщая сумма выручки от реализации автомобилей, тыс. руб.средняя цена одного автомобиля, тыс. руб.
04.0118120,503.021830122,0
17.0125118,709.022651120,5
28.0124116,020.02.4165119,0
26.021232123,2
Определить, на сколько процентов изменилась средняя цена одного грузового автомобиля в феврале по сравнению с январем.
Задача 3.Данные по трем 9-этажным домам, входящим в один жилищный кооператив.ДомОбщая площадь квартир, кв.м.Жилая площадь, %Средняя жилая площадь на 1 жителя, кв.м./чел.Рыночная стоимость 1 кв.м. общей площади, у.е./кв.м.
11975758,5380
21950728,0360
31925707,3340
Определите средние величины всех показателей, приведенных в таблице.
Задача 4.Цехом произведены бракованные детали в трех партиях: в первой партии - 90 штук, что составило 3,0% от общего числа деталей; во второй партии - 140 штук, или 2,8%; в третьей партии - 160 штук, или 2,0%.Определить средний процент бракованных деталей.
Задача 5.Первая бригада получила задание изготовить 2400 деталей, вторая 2200 и третья - 2600 деталей. Первая бригада выполнила план на 100%, вторая на 98% и третья на 106%. Определите процент выполнения задания всеми бригадами в целом.
Задача 6.Имеются следующие данные о заработной плате рабочих завода:N цехабазисный периодотчетный период средняя заработная плата, рубчисленность рабочих, челсредняя заработная плата, рубфонд заработной платы, тыс. руб.
111003001100275
214504001520684
316002001700408
418001002100336
Исчислите среднюю заработную плату рабочего в целом по заводу:1) в базисном периоде;
2) в отчетном периоде. Сравните полученные данные.Укажите, какие виды средних необходимо применить в каждом случае.
Задача 7.Выработка ткани по цехам фабрики характеризуется следующими показателями:N цехабазисный периодотчетный период численность рабочих, челсредняя выработка ткани 1 рабочим, мвыработано ткани всего, мсредняя выработка ткани 1 рабочим, м
14074355579
26085516086
35080456583
Определите среднюю выработку ткани одним рабочим по фабрике в базисном и отчетном периодах. Сравните полученные данные. Укажите, какие виды средних Вы использовали.
Задача 8. В отделе заказов торговой фирмы занято трое работников, имеющих 8-ми часовой рабочий день. Первый работник на оформление одного заказа в среднем затрачивает 14 мин., второй - 15, третий - 19 мин.Определите средние затраты времени на 1 заказ в целом по отделу.
Задача 9. Работа автокомбината за месяц характеризуется следующими данными:автоколоннаобщие затраты на перевозку грузов, рубсредний месячный грузооборот автомашины, ткмсебестоимость одного ткм, коп
120 286460063
247 628540098
317 820440081 Определите по автокомбинату в целом: а) среднюю себестоимость ткм; б) среднее число машин в автоколонне; в) средний месячный грузооборот автомашины.
freedocs.xyz
Тема 3: средние величины.
Задача 1. Заработная плата за неделю у 5-ти рабочих одного цеха составила 6500 руб., 4955 руб., 5323 руб., 5630 руб., 6150 руб.
Определите средний уровень заработной платы рабочих
Решение:
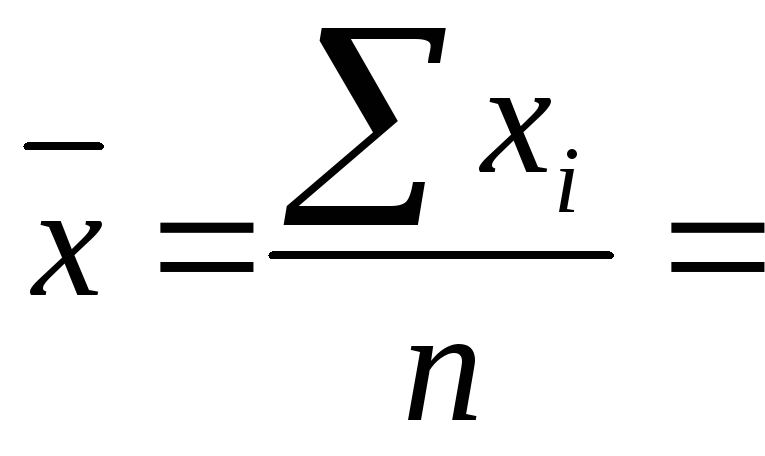
Задача 2. Имеются следующие данные о показателях работы предприятий отрасли за отчетный период:
| Показатель | № предприятия | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Объем продукции, тыс. шт. | 9,0 | 9,8 | 8,5 | 8,6 | 9,1 |
| Стоимость реализованной продукции, тыс. руб. | 1050 | 1070 | 950 | 930 | 960 |
| Прибыль, тыс. руб. | 240 | 290 | 260 | 275 | 220 |
Определите средние уровни каждого показателя по предприятиям отрасли.
Решение:
Задача 3:
Предприятием были выделены одинаковые денежные суммы на приобретение акций 2-х видов, при этом цена вида акций А - 1000 руб., а вида В - 1800 руб. Рассчитайте среднюю цену акции.
Решение:
Так как, в исходных данных совокупные показатели денежной суммы не известны, но сказано, что они одинаковы, а известны только индивидуальные значения признака, то для расчета воспользуемся средней гармонической простой:
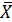 .гарм. =
.гарм. = 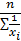 =
=
Задача 4:
Имеются следующие данные о коэффициентах роста среднедушевых доходов населения:
| Годы | 2007 | 2008 | 2009 | 2010 |
| Коэффициент роста | 1,056 | 1,06 | 0,96 | 1,022 |
Определите средний коэффициент роста доходов населения.
Решение:
Так как, в исходных данных представлены относительные величины в виде перечня показателей, то воспользуемся формулой средней геометрической простой:
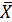 геом. =
геом. = 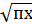 =
=
Задача 5:
Имеются следующие данные по величине товарных запасов, тыс. руб.:
На 01.01.2011 – 53123,6;
На 01.04.2011 – 54165,7;
На 01.07.2011 – 52173,8;
На 01.10.2011 – 55630,2;
На 01.01.2012 – 60886,3.
Задание: определите среднюю величину товарных запасов.
Решение: Так как исходные данные представлены на определённые даты, то используется формула средней хронологической.
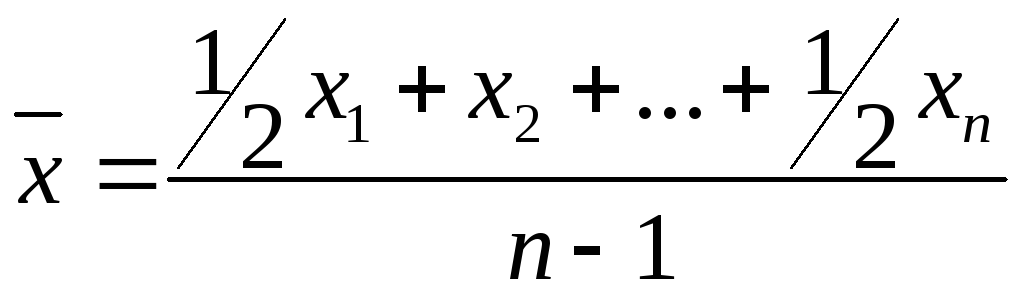 =
=
Задача 6.
Имеются данные об опыте работы предпринимателей:
| Стаж, лет | Число предпринимателей | |
| в сфере обслуживания населения, чел. | в сфере производства, % | |
| 3 4 5 6 7 8 | 16 40 60 50 20 14 | 40 30 18 6 4 2 |
Определите средний стаж предпринимателей по каждой сфере деятельности.
Решение:
Задача 7. Имеются следующие данные
| Рабочие | Произведено деталей за неделю, шт. | Часовая выработка, шт/ч |
| 1-ый | 200 | 10 |
| 2-ой | 240 | 12 |
| 3-й | 390 | 13 |
Задание:
определите следующую выработку одного рабочего
Решение: Так как данные представлены в виде произведения вариант на соответствующие частоты, то используется формула средней гармонической взвешенной:
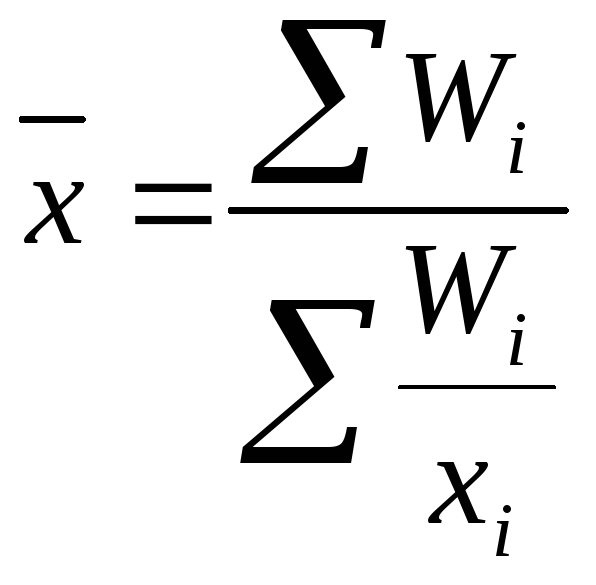
Задача 8:
Продажа подержанных автомобилей на товарной бирже города характеризуется следующими данными:
| Дата торга | Реализовано авто в шт. | Средняя цена авто, в у.е. | Дата торга | Выручка от продажи авто, у.е. | Средняя цена авто, у.е. | ||
| 4.02 | 18 | 120,5 | 3.03 | 1830 | 122 | ||
| 17.02 | 25 | 118,7 | 9.03 | 2650 | 120,5 | ||
| 28.02 | 24 | 116 | 20.03 | 4265 | 119 | ||
| 26.03 | 1232 | 123,2 | |||||
Определите среднюю цену одного авто в феврале и марте, а так же ее абсолютное и относительное изменение.
Решение:
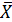 .арифм. =
.арифм. =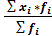 =
= 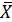 .гарм. =
.гарм. =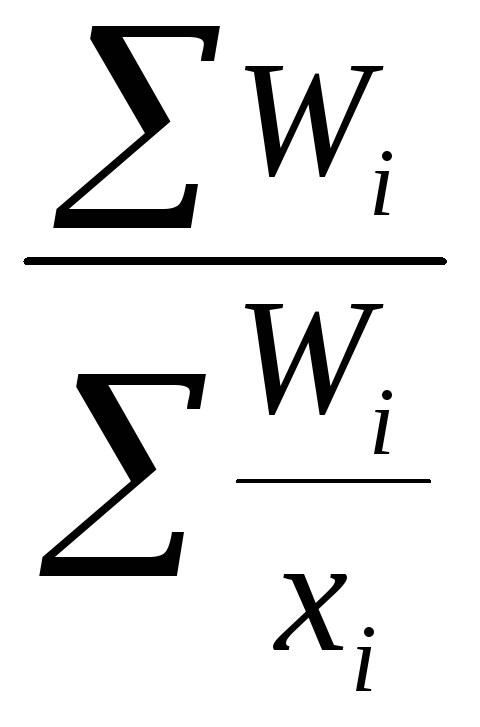 =
=ОПД =
Таким образом, за месяц на товарной бирже средняя цена одного автомобиля ……………………..
Задача 9:
Распределение пенсионеров города по размеру назначенных пенсий с учетом компенсационных выплат на начало года характеризуется данными:
| Размер пенсии, руб. | Удельный вес пенсионеров, % |
| До 2500 2500—3000 3000—3500 3500—4000 Свыше 4000 | 3 15 50 30 2 |
Определите средний размер пенсии, моду и медиану.
Решение:
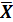 =
=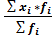
Так как, исходными данными являются интервальные величины, то для перевода их в дискретные необходимо определить середины интервалов, ((нижняя граница интервала + верхняя граница)/ 2).
Для определения середины интервала в открытом интервале к середине интервала предыдущего значения прибавляется величина интервала, (применяется только для рядов с равными интервалами).
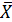 =
=
2. Конкретное значение моды для интервального ряда определяется формулой:
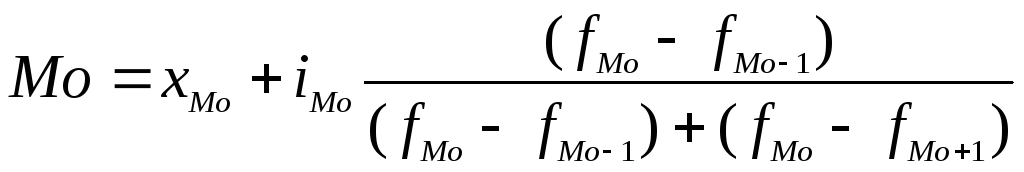
где 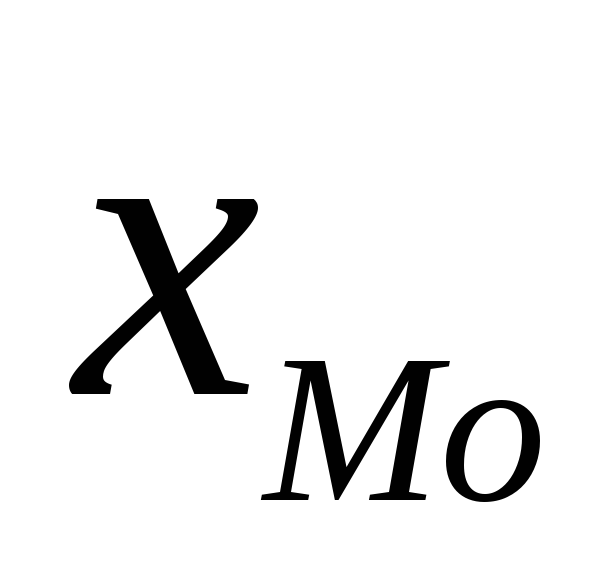 - нижняя граница модального интервала;
- нижняя граница модального интервала;
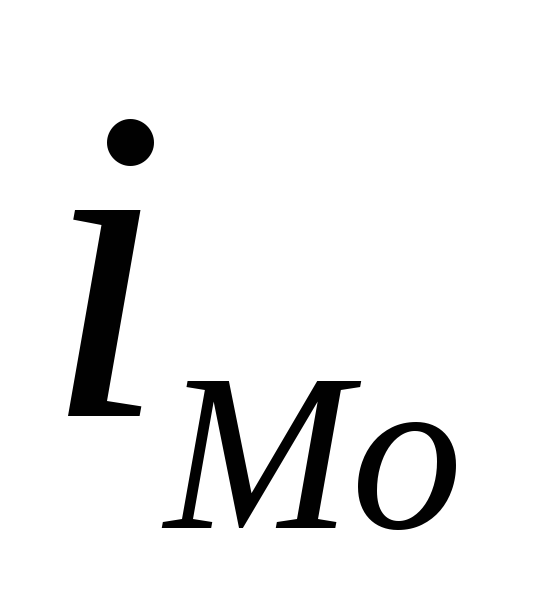 - величина модального интервала;
- величина модального интервала;
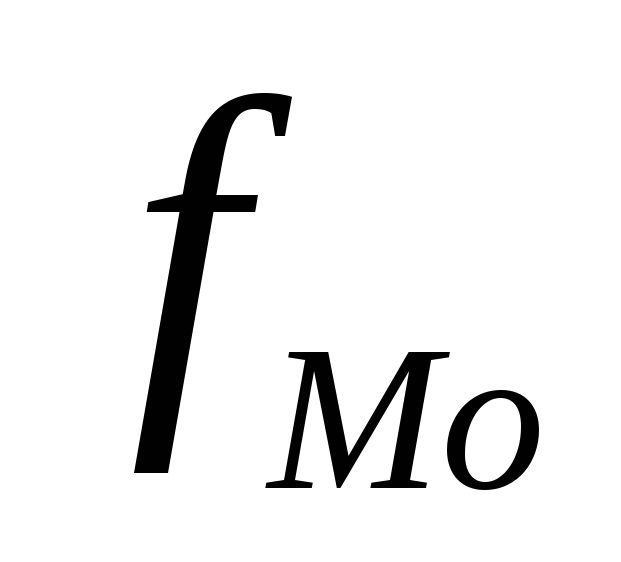 - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу;
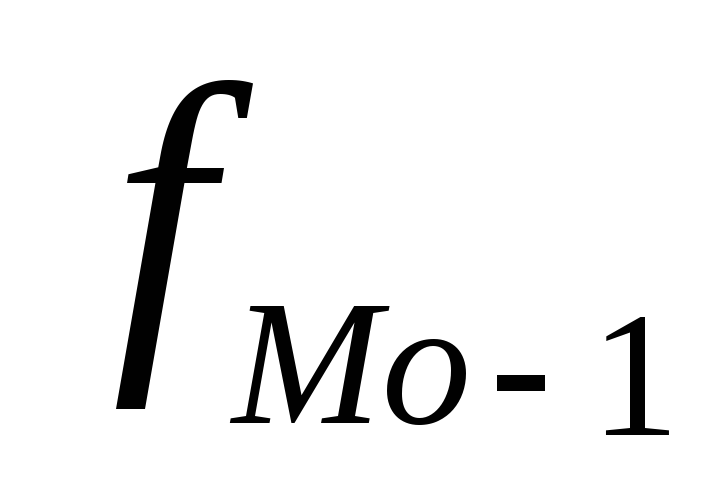 - частота, предшествующая модальному интервалу;
- частота, предшествующая модальному интервалу;
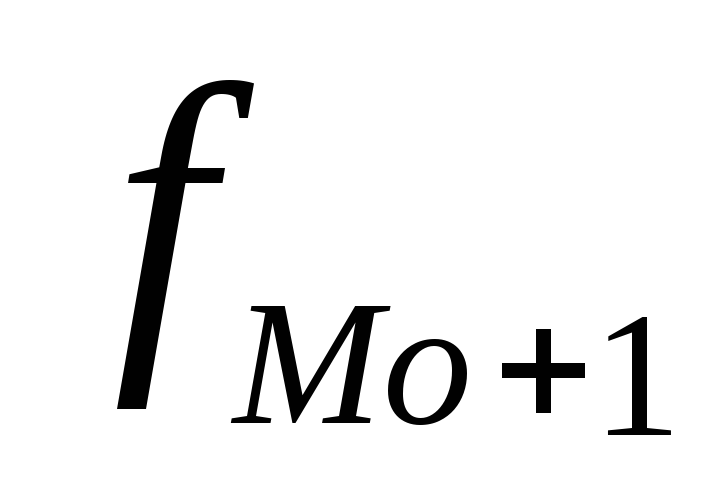 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Мо=
3. Формула медианы в интервальном ряду распределения будет иметь следующий вид:
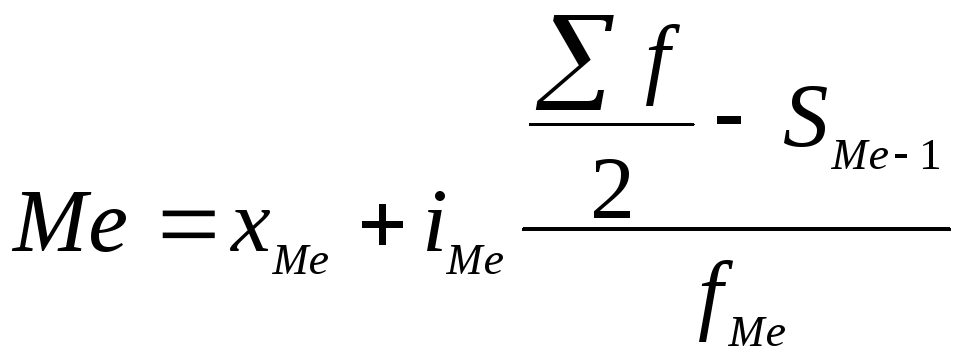
где 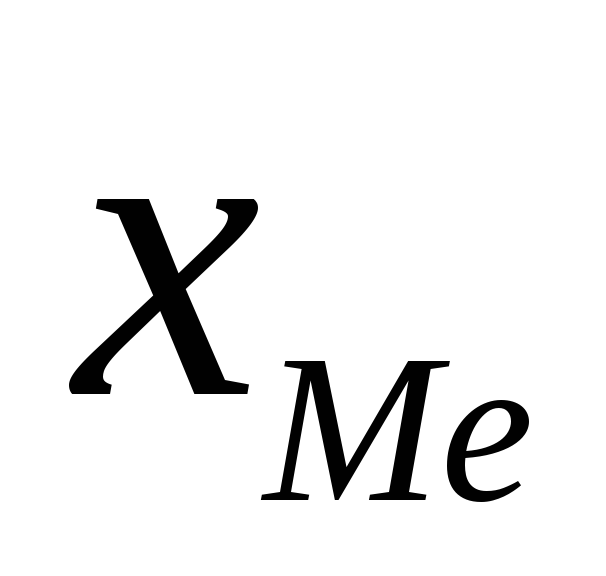 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
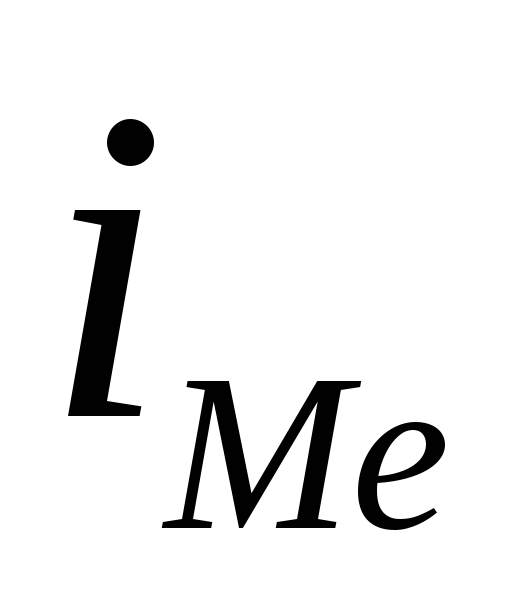 - величина медианного интервала;
- величина медианного интервала;
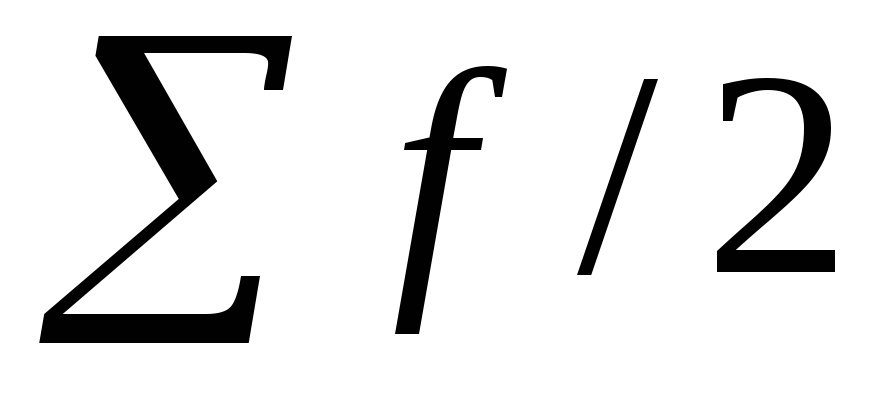 - полусумма частот ряда;
- полусумма частот ряда;
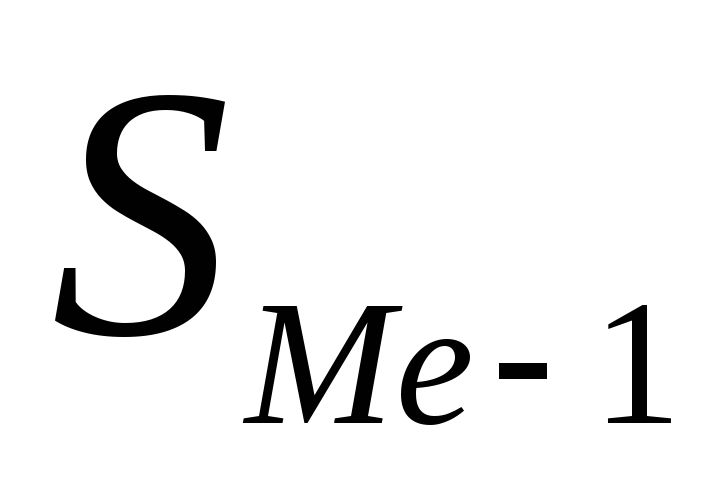 - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу;
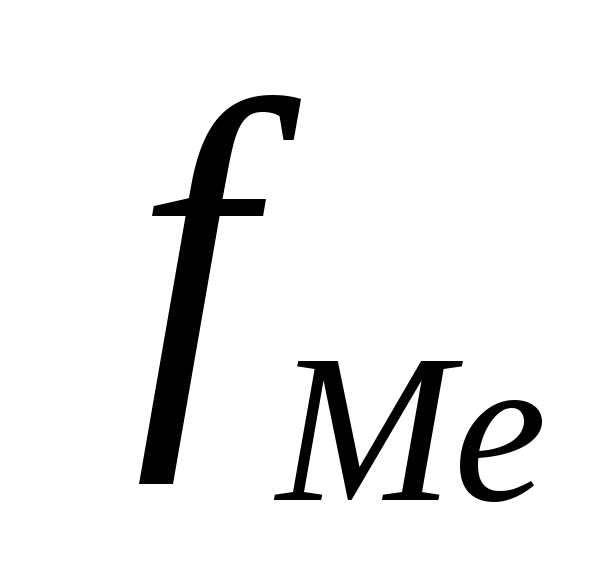 - частота медианного интервала.
- частота медианного интервала.
Найдем медианный доход.
Ме =.
Вывод:
Задача 10:
По данным исследований получены следующие данные по среднедушевому доходу в месяц, руб.:
| № | Среднедушевой доход | Удельный вес домохозяйств, % |
| 1 2 3 4 5 | до 1500 1500-1900 1900-2600 2600-3400 3400 и выше | 10 14 45 29 2 |
Определите среднемесячный доход домохозяйств, моду, медиану.
Решение:
Для преобразования интервального ряда в дискретный, построим вспомогательную таблицу.
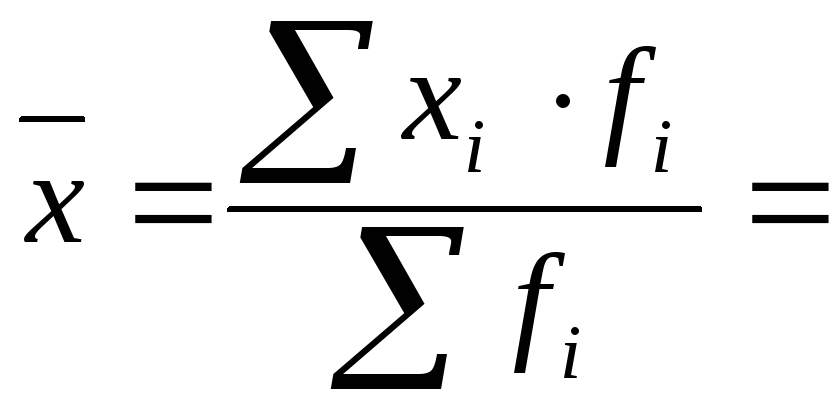
Мо=
Ме =.
Задача 12. Имеются данные о распределении естественной убыли в 200 партиях товара.
| Естественная убыль, % | Количество партий |
| 7-9 | 12 |
| 9-11 | 23 |
| 11-13 | 85 |
| 13-15 | 55 |
| 15-17 | 25 |
| итого | 200 |
Задание: определите средней % естественной убыли, моду, медиану.
studfiles.net
Вариант 21
1. Структурные средние величины.
2. Задача. Продажа грузовых автомобилей КамАЗ-55111 на товарной бирже города характеризуется следующими данными:
| Дата торга | Реализовано автомобилей, шт. | Средняя цена 1 автомобиля, тыс. руб. | Дата торга | Общая сумма выручки от реализации автомобилей, тыс. руб. | Средняя цена 1 автомобиля, тыс. руб. |
| 4.01 | 18 | 120,5 | 3.02 | 1830 | 122,0 |
| 17.01 | 25 | 118,7 | 9.02 | 2651 | 120,5 |
| 28.01 | 24 | 116,0 | 20.02 | 4165 | 119,0 |
| 26.02 | 1232 | 123,2 |
Определить, на сколько процентов изменилась средняя цена одного грузового автомобиля в феврале по сравнению с январем.
3. Тест. Показателями структуры вариационного ряда (структурными средними) являются:
А) простая средняя арифметическая;
Б) средняя арифметическая взвешенная;
В) мода;
Г) медиана;
Д) среднее квадратическое отклонение;
Е) дисперсия;
Ж) дециль;
З) квартиль.
Вариант 22
1. Показатели вариации рядов распределения.
2. Задача. В порядке выборочного наблюдения методом случайного отбора обследован возраст 36 студентов факультета из общего числа 280 человек
Результаты наблюдения следующие:,
| Возраст, лет | 18-20 | 20-22 | 22-24 | 24-26 | 26 - 28 | 28-30 |
| Число студентов | 2 | 10 | 14 | 7 | 2 | 1 |
Определите:
1) средний возраст студентов;
2) с вероятностью 0,954 вычислите предельную ошибку выборки и пределы, в которых будет находиться средний возраст студентов факультета.
3. Тест. Значение моды определяется на основе графика:
А) кривой Лоренца;
Б) полигона распределения;
В) функции распределения;
Г) кумуляты;
Д) огивы.
Вариант 23
1. Виды дисперсий и правило их сложения.
2. Задача. Имеются данные о сроках функционирования коммерческих банков на начало года:
| Срок функционирования, лет | 1 -2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | Свыше 7 |
| Число банков, % | 16 | 20 | 28 | 18 | 10 | 4 | 4 |
Определите:
1) средний срок функционирования банков;
Б) моду и медиану.
3. Тест. Для измерения тесноты корреляционной связи между двумя количественными признаками используются:
А) коэффициент корреляции знаков;
Б) коэффициент эластичности;
В) линейный коэффициент корреляции;
Г) коэффициент корреляции рангов.
Вариант 24
1. Выборочное наблюдение как важнейший источник статистической информации.
2. Задача. Хронометраж операций пайки радиаторов на ремонтном предприятии дал следующие результаты:
| Время пайки, мин | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Итого |
| Количество радиаторов | 2 | 5 | 10 | 17 | 1 | 35 |
Вычислить: а) среднее время пайки радиатора; б) коэффициент вариации. Сформулировать вывод.
3. Тест. Модой называется:
А) наиболее часто встречающееся значение признака в данном ряду;
Б) значение признака, делящее данную совокупность на две равные части;
В) наиболее редко встречающееся значение признака в данном ряду;
Г) серединное значение признака в данном ряду распределения;
Д) среднее арифметическое значение признака в данном ряду распределения.
studfiles.net